Контрольные задачи

Контрольные вопросы

Литература

Основные тождества для операции прямого произведения множеств

Мощность прямого произведения множеств

Пример 13.

AiÎAi (i=1,2,…,n). В случае, если А1=А2=…=Аn=А, то А1´А2´…´Аn = Аn - n-ая декартова степень множества А.

Х – множество точек отрезка [0;1];

Y – множество точек отрезка [1;2];

Z – множество точек отрезка [0;0,5].

X ´ Y ´ Z – множество точек пространства, ограниченного параллелепипедом.

Замечание. Декартово произведение R ´ R ´ R= R ³ представляет собой множество координат точек пространства. Рене Декарт (1596-1650)

французский философ и математик

Теорема. Пусть А₁, А₂, …, А_n – конечные множества мощностью m₁, m₂, …, m_{n .} соответственно, т.е. ½ А₁ ½= m₁,½ A₂ ½= m₂, …,½ A_n ½= m_{n .}. Тогда мощность их прямого произведения равна произведению мощностей множеств – сомножителей, т.е.

½ А₁´А₂´…´А_n ½= m₁*m₂*…*m_n

Следствие: Мощность n -ой декартовой степенимножества А равна n -ой степенимощности этого множества½ Аⁿ ½=½ A ½ ⁿ

1. А ´ В ¹ B ´ A – некоммутативность;

2. А ´(В ´ C) = (А ´ B) ´ C = А ´ B ´ C – ассоциативность слева и справа;

3. А ´ (В È C) = (А ´ В)È(А ´ C) – дистрибутивность по объединению слева;

4. (А È В) ´ C = (А ´ C)È(B ´ C) – дистрибутивность по объединению справа;

5. А ´ (В Ç C) = (А ´ В) Ç (А ´ C) – дистрибутивность по пересечению слева;

6. (А Ç В) ´ C = (А ´ C) Ç (B ´ C) – дистрибутивность по пересечению справа;

7. А ´(В \ C) = (А ´ B) \ (A ´ C) – дистрибутивность по разности слева;

8. (А \ В) ´ C = (А ´ C) \ (B ´ C) – дистрибутивность по разности справа;

9. (А ´ В) Ç (С ´ D) = (А Ç С) ´ (В Ç D).

1. Новиков Ф.А. Дискретная математика для программистов. 3-е изд. СПб.:Питер, 2009.–383 с.

2. Тюрин С.Ф. Дискретная математика: Практическая дискретная математика и математическая логика: учеб. пособие. /С.Ф.Тюрин, Ю.А.Аляев. – М.:Финансы и статистика, 2010. – 384 с.

3. Гладков Л.А., Курейчик В.В., Курейчик В.М.: Дискретная математика: теория множеств, алгоритмом, алгебры логики: Учебное пособие / Под ред. В.М.Курейчика. – Таганрог: изд-во ТТИ ЮФУ, 2009. – 312 с.

4. Нефедов В.Н., Осипова В.А. Курс дискретной информатики: Учеб. пособие. – М.:изд-во МАИ, 1992. – 264 с.

5. Кузнецов О.П. Адельсон-Вельский Г.М. Дискретная математика для инженеров. 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1988. – 480 с.

(основные понятия, положения и формулировки)

(в скобках приведены баллы за правильный и полный ответ)

1. Дать понятие:

- множества (3);

- подмножества (3);

- надмножества (3).

2. Какие способы используются для описания множеств? (2) Привести примеры различных способов описания и дать им пояснения. (5)

3. В чем состоит отличие между счетными и несчетными множествами? (2) Приведите примеры счетного и несчетного множества. (3)

4. Что понимается под мощностью множества? (2) Приведите пример множества А с мощностью | A |=8. (2)

5. Что понимается под абсолютным дополнением некоторого множества? (3)

6. Чему равна мощность булеана множества А, состоящего из шести элементов? (2)

7. Что понимается под взаимным включением множеств и в каком случае оно существует? (2)

8. В чем состоит отличие между строгим и нестрогим включением множеств? (3)

9. Что понимается под собственным подмножеством некоторого множества? (3)

10. Что понимается под свойством рефлексивности (симметричности, транзитивности) отношения? (3) Привести пример (примеры) отношений, обладающих этим свойством. (1 балл за каждый пример)

11. Что понимается под антирефлексивным (антисимметричным, нетранзитивным) отношением? (3) Привести пример (примеры) подобного отношения. (1 балл за каждый пример)

12. Является ли отношение параллельности двух прямых транзитивным? (1) Утверждение обосновать. (3)

13. Дать определение операции объединения (пересечения, разности, симметрической разности, дополнения) множеств. (3)

14. В каком случае объединение (пересечение, разность) двух множеств равно пустому (универсальному) множеству? (2)

15. Привести пример множеств, для которых пересечение равно Æ, а разность не равна Æ. (2)

16. Записать законы де Моргана (поглощения, склеивания, сокращения). (3)

17. Перечислите основные способы (методы) доказательства правомочности тождеств. (3) На чем основан тот или иной способ (метод) доказательства? (3)

18. Что понимается под прямым (декартовым) произведением трех множеств? (3) Чему равна мощность этого произведения? (2)

19. Для множества A= { a, b } найти A³ – третью декартову степень. (3)

20. Записать основные тождества для операции прямого произведения множеств. (2 балла за каждое)

1. Доказать тождества по определению равенства множеств (методом взаимного включения):

а) A Ç(B È C)=(A Ç B) È (A Ç C) (5)

б) A È(Ç B)= A È B (4)

в) A Ç(B − C)=(A Ç B) − (A Ç C) (10)

2. Доказать тождества с использованием других тождеств (алгебраическим способом):

а) A Ç(È B)= A Ç B (2)

б) (А È В)Ç(А È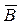)= А (2)

в) A \ (B \ C)=(A \ B)È(A Ç C) (4)

3. С помощью диаграмм Эйлера-Венна (геометрическим способом) показать правомочность тождеств:

а) A Ç(B È C)=(A Ç B)È(A Ç C) (3)

б) A È(Ç B)= A È B (3)

в) 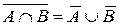(3)

г) A −(B − C)=(A − B)− C (5)

4. Убедится в правомочности тождества: A \(B \ C)=(A \ B)È(A Ç C)

на примере числовых множеств:

A ={ x Î N | x − нечётное и x £ 30},

B ={ x Î N | x делится на 3 и x £ 30},

C ={ x Î N | x делится на 5 и x £ 30}. (6)

5. Записать заданные множества перечислением их элементов:

а) A ={ x Î Z | x ²+2 x -3 < 0} (2)

б) B ={ x Î N ₀| | x +1| £ 5} (3)

в) C ={ x Î Z | 0,1< 3^{1- x} < 100} (5)

г) D ={ x Î Z | −1< log₂|1− x | < 2} (5)

д) F ={ x Î R | sin²2 x =1 и 0 £ x £ 2p} (4)

6. Изобразить на координатной плоскости следующие множества:

а) G ={(x,y) Î R ²| | x − 1| − 1< y < 3 − | x +1|} (5)

б) H ={(x,y) Î R ²| y < x <} (4)

в) K ={(x,y) Î R ²| < y <8+2 x - x ²} (5)

г) L ={(x,y) Î R ²| < y < 2cos x } (4)

7. Действует ли коммутативный закон в отношении операции разности множеств? Утверждение обосновать. (3)

8. Проверить правомочность дистрибутивных законов для операций пересечения и разности (относительного дополнения) множеств с использованием диаграмм Эйлера-Венна (3 балла за каждый) и/или с использованием тождественных преобразований (5 баллов за каждый).

9. Убедиться в правомочности тождества A ´(B \ C)=(A ´ B) \ (A ´ C) на примере заданных множеств: A:{ a,b,c }, B ={ c,d,e }, C ={ a,b,d }. (5)

10. Упростить выражение: ((A È B)Ç C)È( Ç(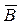È C)) (4)

11. Доказать тождества: а) (A \ B) − (B \ C) − (B \ A) − (C \ B)= A − C (4)

б) (A \ B) È (B \ A)=(B \ A) − (A \ B) (4)

12. Записать множества, приведённые на диаграммах Эйлера-Венна: (3 балла за каждый)

а) б) в) 33))

Дата добавления: 2013-12-13