Отношения между множествами

Способы задания множеств

B(A)={Æ,{a},{b},{c},{a, b},{a, c},{b, c},{a, b, c}}.

Утверждение. Если множество А состоит из n элементов, то множество B (A) всех его подмножеств состоит из 2 ⁿ элементов, т.е. | А |= n ® | B (A)|= 2 ⁿ = 2 ^{| А |}.

Множества могут быть заданы списком, порождающей процедурой, описанием свойств элементов или графическим представлением.

1. Задание множеств списком предполагает перечисление элементов. Например, множество А состоит из букв a, b, c, d: A= { a,b, c, d }или множество L включает цифры 0, 2, 3, 4: L= { 0, 2, 3,4 }.

2. Задание множеств порождающей процедурой означает описание характеристических свойств элементов множества: X = { x | H (x) }, т. е. множество X содержит такие элементы x, которые обладают свойством H (x).

Например:

B = { b | b = p / 2 ± k p, k Î N }, N - множество всех натуральных чисел.

3. Задание множества описанием свойств элементов. Например, M - это множество чисел, являющихся степенями двойки.

К описанию свойств естественно предъявить требования точности и недвусмысленности. Так, "множество всех хороших песен 2010 года" каждый составит по-разному. Надежным способом однозначного задания множества является использование разрешающей процедуры, которая для любого объекта устанавливает, обладает ли он данным свойством и соответственно является ли элементом рассматриваемого множества.

Например, S - множество успевающих студентов. Разрешающей процедурой включения во множество S является отсутствие неудовлетворительных оценок в последней сессии.

4. Графическое задание множеств осуществляют с помощью диаграмм Эйлера-Венна.

Леонард Эйлер (1707-1783) - швейцарский математик, механик, физик и астроном.

Джон Венн (1834-1923) - английский математик и логик.

Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих рассматриваемые множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств. На рис. 1 приведена диаграмма Эйлера-Венна, на которой показаны универсальное множество U и множества A и B.

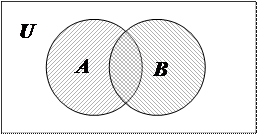
Рис. 1. Пример диаграммы Эйлера-Венна

Два множества A и B могут вступать друг с другом в различные отношения.

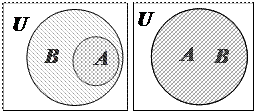
· Множество Aвключено в B, если каждый элемент множества A принадлежит также и множеству B (рис. 2а, 2б.). Частным случаем отношения включения может быть и равенство множеств A и B, что отражается символом Í: A Í B Û " a Î A ® a Î B.

Подобное отношение можно называть нестрогим включением. Довольно часто требуется исключить равенство множеств из отношения включения, в связи с чем вводится отношение строгого включения.

· Множество Aстрого включено в B, если A включено в B, но не равно ему (рис. 2а), что отражается символом Ì: A Ì B Û (A Í B) и (A¹B).

В этом случае множество А называют собственным (строгим, истинным) подмножеством множества В. Примерами использования строгого включения могут являться: A Ì U, B Ì U, ÆÌ B, ÆÌ B.

Отношения между множествами могут обладать следующими свойствами: рефлексивностью, симметричностью и транзитивностью.

Свойство рефлексивности является унарным (одноместным), т.е. применительно к единственному объекту (в данном случае к множеству) и означает, что отношение применимо к «себе самому».

Простым примером рефлексивного отношения для чисел могут служить отношения «³» или «£», т.к. для любого числа d можно записать d ³ d или d £ d. В свою очередь отношения «>» и «<» этим свойством не обладают, в связи с чем они называются антирефлексивными.

Свойство симметричности является бинарным (двухместным), т.е. применимо к двум объектам. Отношение является симметричным, если оно выполняется в обе стороны по отношению к паре объектов (в данном случае множеств). Примерами свойства симметричности являются различные геометрические объекты, для которых понятие «симметрии» является наиболее наглядным. Например, отношение: «быть симметричными относительно оси х» в отношении точек плоскости является симметричным. Действительно, если первая точка симметрична второй, то вторая точка обязательно симметрична первой.

В свою очередь, отношение между двумя объектами не обладает свойством симметричности, т.е. является антисимметричным, если его выполнение в обе стороны имеет место только в случае равенства объектов.

Если записать бинарное отношение между объектами a и b в общем виде aRb, где R – символ отношения, то для симметричного отношения: aRb® bRa при любых a и b, а для антисимметричного aRb® bRa, только, если a = b.

Примером антисимметричного отношения могут служить отношения «³» или «£» между числами. Действительно, (a £ b) ® (b £ a), только, если a = b.

Свойство транзитивности является тернарным (трехместным), т.е. применяется к трем объектам. Отношение R между объектами a, b, с является транзитивным, если из aRb и bRс следует aRс, т.е. из выполнения отношения R между парами объектов (a, b) и (b, с) следует его выполнение и для пары (a, с). Примерами транзитивного отношения для чисел являются отношения «>», «³», «<», «£».

Отношение, не обладающее свойством транзитивности, называется нетранзи-тивным. Примером нетранзитивного отношения между множествами может служить отношение «пересекаться». Действительно для множеств: A= { a, b }, B= { b, c }, C= { c, d } A пересекается с B, B пересекается с C, но A не пересекается с C.

Отношение нестрогого включения обладает свойствами:

- рефлексивности: А Í А;

- антисимметричности: (A Í В и B Í A) ® (A=B);

- транзитивности: (A Í ВиB Ì C) ® (A Ì C).

Отношение строгого включения обладает свойствами:

- антирефлексивности: А Ë А;

- транзитивности: (A Ì ВиB Ì C) ® (A Ì C).

Свойства симметричности или несимметричности для отношения строгого включения не рассматриваются, так как их рассмотрение предполагает случай равенства между объектами отношения.

Для комбинации отношений строгого и нестрогого включений:

- (A Í ВиB Ì C) ® (A Ì C);

- (A Ì ВиB Í C) ® (A Ì C).

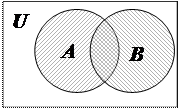а б в с

Рис.2. Возможные отношения множеств А и В

· множество Aравно множеству B, если A и B включены друг в друга или, иначе, между ними существует отношение взаимного включения (рис. 2б.):

A=B Û (A Í B) и (B Í A).

Вторая часть равенства указывает на наиболее типичный метод доказательства равенства множеств A и B, который заключается в доказательстве сначала утверждения АÍВ, а затем ВÍА.

Равные множества содержат одинаковые элементы, причем порядок элементов в множествах не существенен: A ={1, 2, 3} и В ={3, 2, 1} ® A=B.

· множества A и Bне пересекаются, если у них нет общих элементов (рис. 2в.):

Дата добавления: 2013-12-13