Основные тождества (законы) алгебры множеств

Дополнением (абсолютным)множества А называется множество всех тех элементов хуниверсального множества U, которые не принадлежат множеству А (рис. 3 д). Дополнение множества А обозначается:={x çxÏA}=U \ A.

AΔB ={a}È{d}={a,d}.

А\В={а, b, c} \{b,c,d}={a}.

АÇВ={b,c}; AÇC={c}; BÇC={c,d}; AÇBÇC={c}.

Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3в):

A \ B = { x | x Î A иx Ï B }.

Разность множеств А и В иначе называется дополнением множества А до множества В (относительным дополнением).

Пример 4 (для множеств из примера 2).

Симметрической разностью множеств А и В называется множество, состоящее из элементов, которые принадлежат либо только множеству А, либо только множеству В (рис. 3г). Симметрическую разность обозначают как A Δ B,A – B или A Å B:

A Δ B = { x | (x Î A иx Ï B) или (x Î В иx Ï А) }.

Таким образом, симметрическая разность множеств A и B представляет собой объединение разностей (относительных дополнений) этих множеств: A Δ B =(A\B) È (B\A).

Пример 5 (для множеств из примера 2).

С учетом введенной операции дополнения разность множеств А и В можно представить в виде: A \ B = A Ç.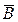

Операции над множествами используются для получения новых множеств из уже существующих. Порядок выполнения операций над множествами определяется их приоритетами в следующем порядке: , \, Ç, È, Δ.

1). Коммутативные (переместительные) законы: A È B= B È A; A Ç B= B Ç A.

2). Ассоциативные (сочетательные) законы:

A È (B È C)=(A È B) È C; A Ç (B Ç C)=(A Ç B) Ç C.

3). Дистрибутивные (распределительные) законы:

A È(B Ç C) = (A È B) Ç(A È C); A Ç (B È C) = (A Ç B) È (A Ç C).

Замечание. Эти законы выражают дистрибутивность объединения относительно пересечения (для первого) или дистрибутивность пересечения относительно объединения (для второго) слева. Операции объединения и пересечения обладают также свойством дистрибутивности справа:

(A È B) Ç C = (A Ç С) È (В Ç C); (A Ç B) È C = (A È С) Ç (В È C);

4). Законы тавтологии (идемпотентности ): A È A= A; A Ç A= A.

5). Законы двойственности (де Моргана):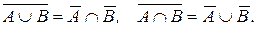

Следствия из законов двойственности:

Дата добавления: 2013-12-13