Оценка аннуитета

Одним из ключевых понятий в финансовых и коммерческих расчетах является понятие аннуитета (annuity). Логика, зало­женная в схему аннуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инве­стиционных проектов, а также в анализе аренды.

Аннуитет представляет собой частный случай денежного по­тока, а именно - это поток, в котором длительности всех пе­риодов равны между собой (напомним, что мы предполагаем либо только притоки, либо только оттоки денежных средств). Исторически вначале рассматривались ежегодные (период равен одному году) денежные поступления, что и послужило основой для названия "аннуитет" (так как год на латинском языке - anno). В дальнейшем в качестве периода стал выступать любой промежуток времени при сохранении прежнего названия. Ан­нуитет еще называют финансовой рентой, или просто рентой. Любое денежное поступление называется членом ренты, а ве­личина постоянного временного интервала между двумя после­довательными денежными поступлениями называется периодом аннуитета (периодом ренты). Если число равных временных интервалов ограничено, аннуитет называется срочным.

Если в течение каждого базового периода начисления про­центов денежные поступления происходят 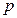раз, то аннуитет часто называют 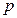-срочным. Часто в качестве такого базового периода выступает календарный год.

Как и в общем случае, выделяют два типа аннуитетов: пост­нумерандо (ordinary annuity) и пренумерандо (annuity due).

Примером срочного аннуитета постнумерандо могут служить регулярно поступающие рентные платежи за пользование сдан­ным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истечении оче­редного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопле­ния достаточной суммы для крупной покупки.

Ситуация, когда денежные поступления по периодам варьи­руют, является наиболее распространенной. В этом случае ан­нуитет называется переменным (variable annuity) и общая поста­новка задачи такова.

Пусть 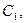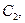..., 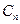- аннуитет, период которого совпада­ет с базовым периодом начисления процентов по ставке . Тре­буется найти стоимость данного аннуитета с позиции будущего и с позиции настоящего.

Прямая задача предполагает оценку с позиции будущего, т.е. на конец периода , когда реализуется схема наращения, кото­рую для аннуитета постнумерандо можно представить.

Таким образом, на первое денежное поступление 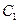начис­ляются сложные проценты за 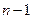период и оно в конце 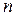-го периода станет равным 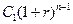. На второе денежное посту­пление 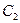начисляются сложные проценты за 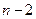периода и оно станет равным 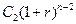и т.д. На предпоследнее денеж­ное поступление 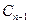проценты начисляются за один период и оно будет в конце 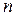-го периода равно 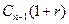. Естественно, на 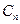проценты не начисляются.

Следовательно, наращенный денежный поток для исходного потока постнумерандо имеет вид

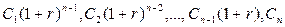
и будущая стоимость 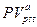исходного денежного потока (ан­нуитета) постнумерандо может быть оценена как сумма нара­щенных поступлений, т.е. получаем формулу:

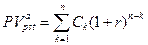(7.1)

или, используя обозначение множителя наращения:

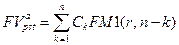(7.2)

Обратная задача подразумевает оценку с позиции текущего момента, т.е. на конец периода 0 (или, что то же самое, на мо­мент начала первого периода). В этом случае реализуется схема дисконтирования, а расчеты необходимо вести по приведенному потоку, все элементы которого с помощью дисконтных множи­телей приведены к одному моменту времени, а именно к на­стоящему моменту времени. Элементы приведенного денежного потока уже можно суммировать; их сумма характеризует приве­денную, или текущую, стоимость аннуитета, которую при необ­ходимости можно сравнивать с величиной первоначальной ин­вестиции.

Таким образом, приведенный денежный поток для исходного потока постнумерандо имеет вид

…,

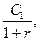
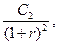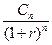
Приведенная стоимость денежного потока (аннуитета) пост­нумерандо 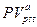в общем случае может быть рассчитана по формуле

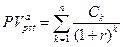(7.3)

Если использовать дисконтный множитель, то формулу (7.3) можно переписать в следующем виде:

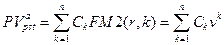(7.4)

Пример:

Рассчитать приведенную стоимость аннуитета постнумеран­до (тыс. тенге): 12, 15, 9, 25, если дана процентная ставка 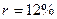и период равен одному году.

Год	Денежный поток, тыс. тенге	Дисконтный множитель при	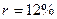Приведенный поток, тыс. тенге
		0,8929	10,71
		0,7972	11,96
		0,7118	6,41
	25	0,6355	15,89
			44,97

Заметим, что формула (7.1) является частным случаем урав­нения эквивалентности при 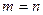, , 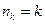, , 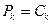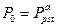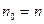. Следовательно, оценку будущей стоимости аннуитета можно рассматривать с точки зрения ситуации, когда платежи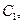 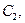…,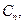выплачиваемые соответственно в конце первого, второго, …, -го периода, заменяются одним платежом 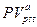с выплатой в конце -го периода. Аналогичным образом в указанных обозначениях только при 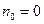получает­ся формула (7.3), т.е. исходный поток платежей заменяется од­ним платежом 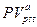с выплатой в конце нулевого периода.

Формулу (7.3) можно получить, не указывая явным образом приведенный денежный поток, а осуществляя приведение вели­чины 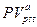к настоящему моменту времени. Действительно

.

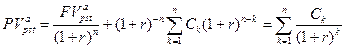Логика оценки аннуитета пренумерандо аналогична описан­ной; некоторое расхождение в вычислительных формулах объ­ясняется сдвигом элементов потока к началу соответствующих подынтервалов.

Следовательно, наращенный денежный поток имеет вид

,

и будущая стоимость исходного денежного потока (аннуитета) пренумерандо 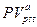в общем виде может быть рассчитана по формуле

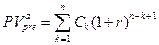(7.5)

Очевидно, что .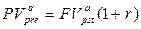

Приведенный денежный поток для исходного потока прену­мерандо имеет вид

Следовательно, приведенная стоимость потока пренумерандо 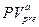может быть рассчитана по формуле

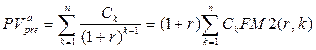(7.6)

Как и в случае с будущей стоимостью, очевидно, что 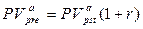. Так, если в предыдущей задаче предполо­жить, что исходный поток представляет собой поток пренуме­рандо, то его приведенная стоимость будет равна:

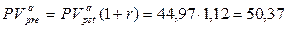тыс. тенге.

Дата добавления: 2014-01-04