Метод депозитной книжки

Год	Остаток ссуды на начало года	Сумма годового платежа	В том числе	Остаток ссуды на конец года
проценты за год	погашенная часть долга
	20 000	5 687	2 600	3 087	16 913
	16 913	5 687	2 199	3 488	13 425
	13 425	5 687	1 745	3 942	9 483
	9 483	5 687	1 233	4 454	5 029
	5 029	5 687		5 029

Данная таблица позволяет ответить на целый ряд дополни­тельных вопросов, представляющих определенный интерес для прогнозирования денежных потоков. В частности, можно рас­считать общую сумму процентных платежей, величину про­центного платежа в 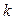-м периоде, долю кредита, погашенную в первые 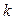лет, и т.д.

Рассуждения, аналогичные используемым при решении при­мера, можно провести и в общем виде, что позволит дать более строго интерпретацию приведенной стоимости аннуитета с по­мощью метода депозитной книжки и попутно выявить полезные с финансовой точки зрения закономерности, позволяющие отве­тить на многие вопросы, связанные с денежными потоками.

Итак, пусть получена ссуда в сумме 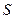на лет под про­центную ставку , причем сложные проценты начисляются на непогашенный остаток. Определим величину годового платежа при возврате долга равными суммами в конце каждого года.

Обозначим через А годовой платеж. В конце первого года часть его, равная 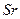, идет на уплату процентов. Оставшаяся же часть 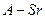- на уплату части долга. Таким образом, к концу первого года величина непогашенного остатка составит: .

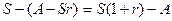В конце второго года на уплату процентов пойдет уже вели­чина 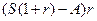, а на уплату долга - 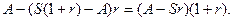Следовательно, к концу второго года долг бу­дет равен:

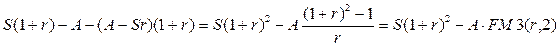
В конце третьего года проценты и уплата долга соответст­венно составят:

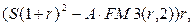
следовательно, остаток долга станет равным:

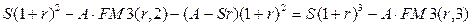
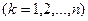Вообще можно доказать, что в конце -го года (проценты, уплата долга и непогашенный остаток соответствен­но составят:

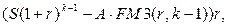(7.42)

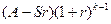, (7.43)

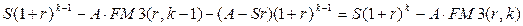(7.44)

Поскольку долг должен быть выплачен через лет, то спра­ведливо равенство 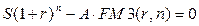, откуда

.

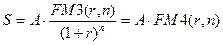Следовательно, 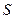является приведенной стоимостью посто­янного аннуитета постнумерандо с членом, равным А, т.е.

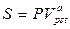
Используя значения (7.42) - (7.44), можно различным обра­зом характеризовать денежные потоки. Например, найти сумму процентных платежей за 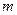лет :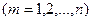

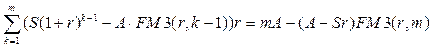
откуда, в частности, следует, что доля кредита, погашенная в первые 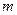лет, составит 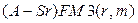, что, конечно, можно получить и непосредственно с помощью (7.43).

Проверим некоторые вычисления приведенного примера. Поскольку для него 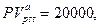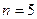, 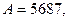то из (7.42) можно найти величину процентного платежа в четвертом пе­риоде:

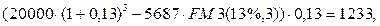
что совпадает с соответствующим значением в таблице 8.

Дата добавления: 2014-01-04