Оценка постоянного аннуитета постнумерандо

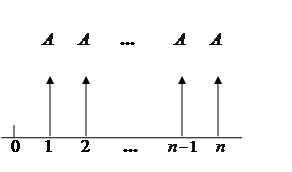
Аннуитет называется постоянным (fixed annuity), если все денежные поступления равны между собой. В этом случае

		Аннуитет пренумерандо Аннуитет постнумерандо

Рис. 7. Виды постоянных аннуитетов

Для оценки будущей и приведенной стоимости аннуитета можно пользоваться рассмотренными в предыдущем параграфе вычислительными формулами; вместе с тем благодаря специфи­ке постоянных аннуитетов в отношении равенства денежных поступлений эти формулы могут быть существенно упрощены. При выводе всех формул этого раздела предполагаем, что де­нежные поступления происходят в течение периодов, кото­рые являются базовыми для начисления процентов по ставке .

Прямая задача оценки срочного аннуитета при заданных ве­личинах регулярного поступления 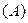и процентной ставке 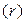предполагает оценку будущей стоимости аннуитета 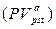. Как следует из логики, присущей схеме аннуитета, записанный в порядке поступления платежей наращенный денежный поток (в аннуитете постнумерандо) имеет вид:

, ,…, , ,

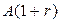а формула (7.1) трансформируется следующим образом:

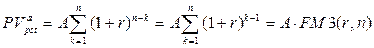(7.7)

Входящий в формулу множитель 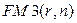называется ко­эффициентом наращения ренты (аннуитета) и представляет собой сумму первых членов геометрической прогрессии, на­чинающейся (в обозначениях первого раздела) с и имею­щей знаменатель .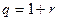

Таким образом,

(7.8)

Из (7.8) следует, что

.

Экономический смысл множителя 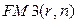заключается в следующем: он показывает, чему будет равна суммарная вели­чина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель 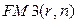часто используется в финансовых вычис­лениях. Его значения зависят лишь от процентной ставки 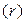и срока действия аннуитета, причем с увеличением каждого из этих параметров величина 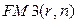возрастает. Значения множителя для различных сочетани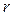й и можно табулировать. Заметим, что при выводе фор­мулы (7.7) использовали выражение процентной ставки 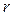в де­сятичных дробях.

Из (7.7) следует, что 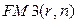показывает, во сколько раз наращенная сумма аннуитета больше величины денежного по­ступления 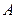. В связи с этим множитель 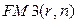называют также коэффициентом аккумуляции вкладов.

Заметим, что формула (7.7) охватывает и "пограничные" слу­чаи. Так, при одном денежном поступлени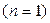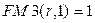и и 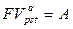. А при 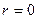(не происходит никаких начислений) из (7.7) получаем , т.е. денежные посту­пления просто суммируются. Естественно, эти результаты сле­дуют и просто из здравого смысла. Иногда для удобства написа­ния формул рассматривают и случай (денежные поступ­ления отсутствуют) и полагают .

Пример:

Вам предлагают сдать в аренду участок на три года, выбрав один из двух вариантов оплаты аренды: а) 10 тыс. тенге в конце каждого года; б) 35 тыс. тенге в конце трехлетнего периода. Ка­кой вариант более предпочтителен, если банк предлагает 20% годовых по вкладам?

Первый вариант оплаты как раз и представляет собой аннуи­тет постнумерандо при 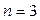и тыс. тенге. В этом случае имеется возможность ежегодного получения арендного платежа и инвестирования полученных сумм как минимум на условиях 20% годовых (например, вложение в банк).

Таким образом, расчет показывает, что вариант (а) более вы­годен.

В формуле (7.7) переменная означает число периодов, а представляет собой ставку за период. И период, конечно, не обязательно должен быть равен одному году. Так, если в каче­стве периода понимать один квартал, то является сложной ставкой за один квартал.

Коэффициент наращения ренты 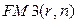обладает рядом свойств, которые можно получить математически и которые имеют содержательную финансовую интерпретацию. Например, для любого целого справедливо равенство

(7.9)

Это соотношение нетрудно доказать алгебраически, но оно также следует и из финансовых соображений. Действительно, величину срочного аннуитета в одну денежную единицу со сро­ком действия можно найти путем сложения наращенной сложными процентами за время величины аннуитета за пер­вые периодов и величины аннуитета за оставшиеся 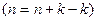периодов. Если же в качестве первых взять пе­риодов, а оставшиеся будут периодами, то из такого же фи­нансового смысла следует

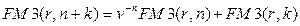(7.10)

что математически достаточно очевидно в силу симметричности вхождения параметров и в формулу (7.9). Также из формулы (7.8) следует равенство

которое позволяет высказать следующую интерпретацию ре­зультата наращения сложными процентами. Наращенная слож­ными процентами по ставке г одна денежная единица через периодов численно равна сумме этой денежной единицы и бу­дущей стоимости аннуитета постнумерандо с денежными по­ступлениями, равными (величина процента от одной денеж­ной единицы за период), т.е. будущая стоимость этого аннуитета совпадает с величиной сложных процентов, начисленных на од­ну денежную единицу. Заметим, что указанное выше равенство можно, очевидно, записать и в виде

Поскольку оценка срочных аннуитетов важна при анализе финансовых операций, получим формулы, аналогичные (7.7), для различных видов аннуитетов. При этом мы убедимся, что при выводе этих формул соответствующие рассуждения прин­ципиально не отличаются друг от друга. К тому же умение про­водить такие рассуждения весьма полезно при решении задач.

Если является процентной ставкой (в десятичных дробях) за базовый период, а начисление сложных процентов происходит 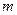раз в течение этого периода (не пишем , поскольку период в принципе"может отличаться от года), то наращенный денежный поток, начиная с последнего денежного поступления, имеет вид

…,

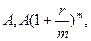
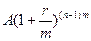
Другими словами, получили геометрическую прогрессию,
первый член которой равен и знаменатель - Следовательно, сумма первых членов этой прогрессии равна:

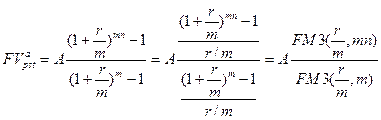(7.11)

Ситуацию, когда в течение базового периода начисления процентов денежные поступления происходят несколько раз, а проценты начисляются один раз в конце периода, можно рас­сматривать с двух точек зрения. Изложим первую из них.

Пусть в течение базового периода денежные поступления происходят 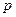раз и один раз в конце периода начисляются про­центы в соответствии со ставкой .

Определим сумму, которая накопится к концу любого перио­да, если на отдельные взносы, поступающие в течение периода, начисляются сложные проценты.

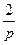На последнее поступление проценты не начисляются и оно остается равным . На предпоследнее поступ­ление начисляются сложные проценты за -ю часть периода и оно будет равно . На -е поступление начисляются сложные проценты за -ю часть периода и оно будет равно и т.д. до первого включительно, которое будет равно 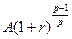. Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом А, знаменателеми числом членов, равным 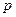, поэтому сумма этих величин равна:

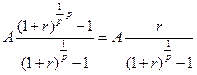
Таким образом, можно считать, что имеем аннуитет, в котором денежные поступления равны величине 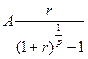и происходят в конце каждого базового периода начисления процен­тов. Поэтому, пользуясь (7.7), получим:

А учитывая (7.8), можно написать

(7.12)

Заметим, что, поскольку , значения 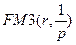в приложении 3 не указаны. Однако непосредственно по формуле (7.8) эти значения нетрудно вычислить с помощью микрокалькулятора.

Теперь изложим другую точку зрения, полагающую, что на отдельные взносы, поступающие в течение периода, начисляют­ся простые проценты. Определим в этом случае сумму, которая накопится к концу любого периода.

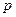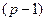Естественно, последнее -е поступление останется рав­ным . На предпоследнее -е поступление начисляются простые проценты за -ю часть периода и оно будет равно . Аналогичным образом -е (р-2)-е поступление станет равным и т.д. Наконец, первое поступление станет равным . Полученные величины образуют арифметическую прогрессию (разность равна ; число членов - 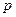), следовательно, их сумма равна:

.

Полагая, что имеем аннуитет, в котором денежные поступления в каждом пepиоде равны величине , и, пользуясь (7.7), получим

(7.13)

Формулы (7.12) и (7.13) отличаются друг от друга, так как при начислении процентов использовали два подхода и (7.13) доставляет большее значение, чем (7.12), поскольку внутри ба­зового периода осуществляется начисление по простым процен­там. При 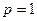как из (7.12), так и из (7.13) следует (7.7).

Аналогичным образом можно рассмотреть и самую общую ситуацию, когда в течение базового периода денежные поступ­ления происходят 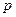раз и проценты начисляются 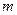раз за пе­риод. Например, если начисляются только сложные проценты, то, как и ранее, определяем вначале сумму, образовавшуюся в конце любого периода. Последнее 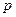-е поступление в периоде остается равным А. Предпоследнее -e поступление после начисления сложных процентов составит 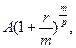-е поступление - и т.д. до первого, которое станет равным 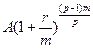. Находим сумму полученных величин:

.

Считая, что есть аннуитет с денежными поступлениями, рав­ными полученной сумме, воспользуемся формулой (7.11):

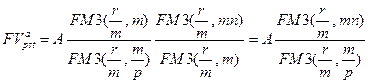(7.14)

Заметим, что при начислении на отдельные поступления внутри периода простых процентов (согласно их свойству) для 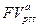и в этом случае получим опять формулу (7.13).

Пример:

Пусть в условиях предыдущего примера о сдаче участка в аренду предлагается оплата по 5 тыс. тенге в конце каждого по­лугодия. При этом возможно начисление процентов: 1) ежегод­ное; 2) полугодовое; 3) ежеквартальное. Оценить, что выгоднее.

В первой ситуации возможны два варианта. Если начисляют­ся только сложные проценты, то по (7.12) при 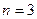, , 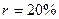получим:

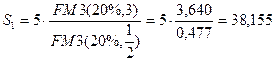тыс. тенге.

Во второй ситуации можно воспользоваться (7.7), считая периодом полугодие. Тогда 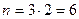, и

тыс. тенге

И в третьей ситуации, пользуясь (7.14), при 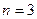, , 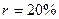, , 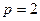получим:

тыс. тенге.

Очевидно, что при решении этой задачи можно было пользо­ваться только общей формулой (7.14), выбирая соответствую­щие значения параметров.

Преобразуем формулу (7.14), предполагая, что длительность базового периода начисления процентов равна одному году, и используя понятие эффективной годовой процентной ставки .

Так как , то

Пользуясь этими соотношениями, получим:

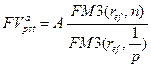(7.15)

Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо 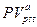выводится из основной формулы (7.3) и имеет вид:

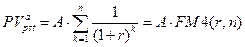(7.16)

Множитель 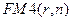называется коэффициентом дискон­тирования ренты (аннуитета) и как сумма членов геометриче­ской прогрессии равен величине:

(7.17)

Экономический смысл дисконтного множителя 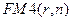заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярными денеж­ными поступлениями в размере одной денежной единицы, продолжающегося равных периодов с заданной процентной ставкой . Значения этого множителя также табулированы и, как для других множителей, процентная ставка дана в процентах.

Дисконтный множитель 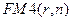полезно интерпретиро­вать и как величину капитала, поместив который в банк под сложную процентную ставку г, можно обеспечить регулярные выплаты в размере одной денежной единицы в течение пе­риодов (выплаты производятся в конце каждого периода). Дей­ствительно, к концу первого периода величина 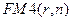станет равной:

В конце первого периода одна денежная единица будет вы­плачена и останется капитал 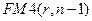, который в конце второго периода станет равным:

После выплаты денежной единицы останется капитал . Продолжая рассуждения аналогичным образом, убеждаемся, что в конце -ro периода будем иметь капи­тал, равный:

После выплаты одной денежной единицы капитал , очевидно, обеспечит выплату последней денежной единицы в конце -го периода.

Например, поскольку , то, поместив 4 тенге 16 тиын под сложную процентную ставку 15%, можно обеспечить выплаты по 1 тенге в конце каждого года в течение 7 лет.

Из вида выражения (7.17) следует, что при возрастании про­центной ставки величина дисконтного множителя 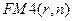уменьшается и, таким образом, уменьшается величина приве­денной (текущей) стоимости.

В формуле (7.16), как и в формуле (7.7), переменная озна­чает число периодов, которые необязательно равны году, что позволяет при соответствующем понимании ставки пользо­ваться этой формулой в различных ситуациях.

Коэффициент дисконтирования ренты 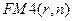удовлетво­ряет соотношениям, подобным (7.9) и (7.10). Равенства для 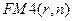можно вывести аналогичным образом, как и для 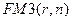. Укажем еще один на первый взгляд формальный ма­тематический прием, тем не менее отражающий финансовый подход. Из (7.17) следует, что 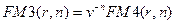. Подставляя это выражение в (7.9) и (7.10), получим

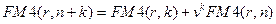(7.18)

(7.19)

Эти соотношения, как и (7.9), (7.10), имеют простой финан­совый смысл. Например, равенство (7.18) означает, что приве­денную стоимость срочного аннуитета в одну денежную едини­цу со сроком действия можно найти путем сложения при­веденной стоимости аннуитета за первые к периодов и учтен­ной за время к приведенной стоимости (на момент начала -го периода) аннуитета за оставшиеся периодов.

Из формулы (7.17) следует, что

,

или используя обозначение дисконтного множителя,

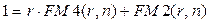
Это равенство можно пояснить, например, таким образом: долг в одну денежную единицу можно погасить равными пла­тежами в денежных единиц в конце периодов от 1 до -го, а в конце -го периода необходимо выплатить 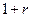денежных единиц.

Вообще в случае рассмотрения только сложных процентов выводы формул для нахождения приведенных стоимостей ан­нуитетов аналогичны выводам формул для нахождения нара­щенных сумм. Получающиеся при рассуждениях денежные по­токи будут представлять собой геометрические прогрессии, знаменателями которых будут соответствующие дисконтные множители. Так, для постоянного аннуитета постнумерандо с начислением сложных процентов 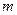раз за базовый период при­веденный денежный поток имеет вид

…,

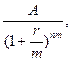
следовательно, сумма этих величин (приведенная стоимость ан­нуитета) равна:

(7.20)

Для 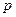-срочных аннуитетов с начислением сложных процен­тов соответственно один раз за базовый период и т раз за базо­вый период можно получить

(7.21)

(7.22)

Как видно, формулы (7.20) - (7.22) похожи соответственно на формулы (7.11), (7.12), (7.14). Применяя эффективную годо­вую процентную ставку , получим:

Поэтому из (7.22) следует, что

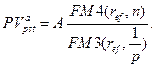(7.23)

Соотношение (7.23) по виду совпадает с (7.21), что объясня­ется содержанием понятия эффективной ставки.

Пример:

Страховая компания, заключив на 4 года договор с некоторой фирмой, получает от нее страховые взносы по 20 тыс. тенге в конце каждого полугодия. Эти взносы компания помещает в банк под 12% годовых. Найти приведенную стоимость суммы, которую получит страховая компания по данному контракту, если проценты начисляются: 1) раз в полгода, 2) ежемесячно.

Будем пользоваться только формулой (7.22). В первом случае , , 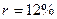, 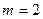. Поэтому

тыс. тенге.

Найдем зависимость между будущей и приведенной стоимо­стями 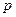-срочного аннуитета постнумерандо с начислением сложных процентов 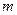раз за период. Из формул (7.14) и (7.22) имеем:

Поскольку из формулы (7.17) следует, что

,

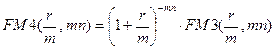после простых алгебраических преобразований получим:

(7.24)

Рассмотрим коротко некоторое обобщение аннуитета, когда первый из потока платежей начинает поступать через h перио­дов. Такой аннуитет называется отсроченным (deferred annuity). Пусть, например, платежи поступают в течение периодов и сложные проценты по ставке начисляются один раз в конце базового периода, совпадающего с периодом аннуитета.

Стоимость этого аннуитета на начало периода, когда посту­пает первый платеж, находим по формуле (7.16) и затем, осуще­ствляя учет полученной величины за h периодов, определяем приведенную стоимость отсроченного аннуитета на начальный момент времени:

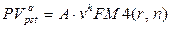(7.25)

В формуле (7.25) h не обязательно должно быть целым чис­лом. А вот если оно целое, то из (7.18) при к = h следует:

и (4.25) примет вид:

(7.26)

т.е. приведенная стоимость отсроченного аннуитета представля­ет собой разность приведенных стоимостей аннуитетов с плате­жами, начиная с первого периода.

Очевидно, что при h = 0 из формулы (7.25) следует (7.16).

Пример:

Банк предлагает ренту постнумерандо на 10 лет с ежеквар­тальной выплатой 100 долл. Годовая процентная ставка в тече­ние всего периода остается постоянной. По какой цене можно приобрести такую ренту, если выплаты начнут осуществляться: а) немедленно; б) через 2 года; в) через 3,5 года, а процентная ставка равна 2, 4, 12% годовых?

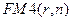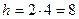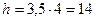Определим приведенную стоимость ренты во всех случаях. Считаем, что число периодов . Тогда ставка за пе­риод будет соответственно 0,5, 1, 3%. В случае а) пользуемся формулой (7.16), определяя либо по таблице, либо непосредственно по (7.17). В случаях б) и в) полагаем и и пользуемся (7.25) или (7.26).

Результаты расчетов для наглядности представим в виде таблицы:

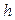
0,5%	1%	3%
	36,1722	32,8347	23,1148
	34,7573	30,3223	18,2470
	33,7326	28,5650	15,2815

Из таблицы видно, что с ростом процентной ставки и срока, после которого начнутся выплаты, приведенная стоимость уменьшается. В частности, если выплаты начнутся через 3,5 го­да и процентная ставка составит 12% годовых, то ренту можно приобрести за 1528,15 долл. (или, конечно, дешевле).

Формулы (7.14) и (7.22) позволяют оценить ренту постнуме­рандо при декурсивном начислении процентов. При антисипативном начислении процентов по сложной учетной ставке d наращенный денежный поток (при , 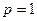), начиная с по­следнего денежного поступления, примет вид:

…,

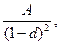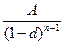
и, следовательно,

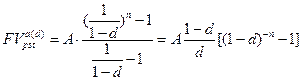(7.27)

Отсюда следует, что

(7.28)

Формулы, отражающие другие виды рент при антисипативном начислении процентов, получаются аналогичным образом.

Пример:

Оценить стоимость трехгодичной ренты с ежемесячной вы­платой 30 долл., если также ежемесячно начисляются антисипативные проценты по сложной учетной ставке 6% годовых.

Полагая 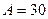, , 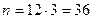, по (7.28) получим:

долл.

Если начисляются непрерывные проценты, то для получения формул определения будущей или приведенной стоимости ан­нуитета необходимо перейти к пределу при 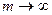, например, в формулах (7.14), (7.22). Так, из (7.14) следует, что для непре­рывных процентов

(7.29)

где 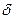- сила роста.

Эту формулу можно получить, подставив в (7.12) вместо ставки эквивалентную ей силу роста 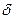. Исполь­зуя (7.29), можно найти приведенную стоимость аннуитета:

(7.30)

При заключении некоторого контракта может быть уже задана, а надо определить, например, величину А разовых де­нежных поступлений. В этом случае из (7.14) при заданных зна­чениях остальных параметров легко получить:

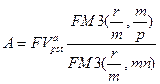
Если же известна приведенная стоимость , то из (7.22) следует, что

.

Например, если известны будущая стоимость 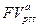аннуите­та, величина А разового годового платежа и процентная ставка , из (7.7), учитывая (7.8), путем преобразований получим фор­мулу для расчета срока аннуитета:

Аналогичным образом можно получить формулы для опре­деления сроков постоянных аннуитетов других видов. Расчет процентной ставки при известных остальных параметрах аннуи­тета требует применения интерполяционных формул.

Пример:

Некоторое предприятие хочет создать фонд в размере 200 тыс. тенге. С этой целью в конце каждого года предприятие предполагает вносить по 50 тыс. тенге в банк под 18% годовых. Найти срок, необходимый для создания фонда.

Используя последнюю формулу этого раздела, получим:

года

Пример:

Работник заключает с фирмой контракт, согласно которому в случае его постоянной работы на фирме до выхода на пенсию (в 65 лет) фирма обязуется перечислять в конце каждого года в течение 20 лет на счет работника в банке одинаковые суммы, которые обеспечат работнику после выхода на пенсию ежегод­ные дополнительные выплаты в 6000 тенге в течение 15 лет. Ка­кую сумму каждый год должна перечислять фирма, если работ­нику 45 лет и предполагается, что банк гарантирует годовую процентную ставку 10%?

Считая, что работник дополнительные выплаты будет полу­чать в конце года, вначале по формуле (7.16) определяем приве­денную стоимость аннуитета длительностью 15 лет в сумме 6000 тенге на момент выхода работника на пенсию:

тенге

Полученная величина представляет собой необходимую бу­дущую стоимость ежегодных вкладов фирмы на счет работника. Поэтому размер каждого вклада можно найти из (7.7), полагая :

тенге.

Таким образом, каждый год фирма должна перечислять на счет работника 797 тенге.

Дата добавления: 2014-01-04