Коэффициенты дисконтирования аннуитета

Срок 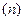аннуитета
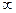
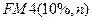
	9,7791	9,9148	9,9672	9,9873	9,9981

Из таблицы видно, что при сроке аннуитета, превышающем 50 лет, коэффициенты дисконтирования аннуитета незначитель­но отличаются друг от друга. Заметим, что с ростом процентной ставки величина срока, начиная с которого коэффициенты 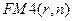перестают сильно отличаться друг от друга, умень­шается (например, при 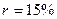такой срок равен 40 годам). Та­ким образом, при больших сроках аннуитета и большом уровне процентной ставки для определения приведенной стоимости срочного аннуитета можно воспользоваться формулой для оп­ределения приведенной стоимости бессрочного аннуитета, при этом полученный приблизительный результат будет не слишком отличаться от точного значения.

Записав (7.45) в виде 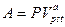, можно сделать вывод, что член бессрочного аннуитета равен процентам "со 100" от приве­денной стоимости этого аннуитета.

Формула (7.45) используется для оценки целесообразности приобретения бессрочного аннуитета, если известен размер де­нежного поступления за период. В качестве обычно принима­ется гарантированная процентная ставка (например, процент, предлагаемый государственным банком).

Пример:

Определить текущую (приведенную) стоимость бессрочного аннуитета постнумерандо с ежегодным поступлением 4,2 тыс. руб., если предлагаемый государственным банком процент по срочным вкладам равен 14% годовых.

По формуле (7.45) находим:

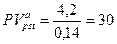тыс. тенге.

Следовательно, если аннуитет предлагается по цене, не пре­вышающей 30 тыс. тенге, он представляет собой выгодную инве­стицию.

С помощью (7.45) можно определить истинную стоимость обыкновенной акции в том случае, когда выплачиваются одина­ковые дивиденды (равные А) в течение всего времени. При этом предположении темп роста дивидендов равен нулю и соот­ветствующая модель называется моделью нулевого роста (zero-growth model). Такая ситуация в определенном смысле свойст­венна привилегированным акциям высокого качества, выплаты дивидендов по которым одинаковы, регулярны и не зависят от величины прибыли на одну акцию, а время обращения привиле­гированных акций не ограничено.

Пример:

Компания гарантирует выплату дивидендов в размере 6 тыс. тенге на акцию в конце каждого года в течение неопределенно долгого времени. Имеет ли смысл покупать акции этой компа­нии по цене 35 тыс. тенге, если можно поместить деньги на депо­зит под 15% годовых?

Поскольку из (7.45) следует, что истинная стоимость акции составляет 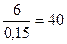тыс. тенге, то акции можно приобретать.

Из формулы (7.17) следует, что

,

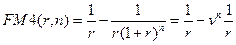и, следовательно, пользуясь обозначением в (7.45), получим:

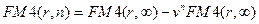(7.46)

Таким образом, приведенная стоимость аннуитета с плате­жами в одну денежную единицу в течение периодов при за­данной процентной ставке равна разности приведенных стои­мостей двух бессрочных аннуитетов, один из которых немед­ленный, а второй - отсроченный на периодов.

Переходя в (7.22) к пределу при 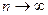, для бессрочного ан­нуитета постнумерандо с денежными поступлениями 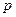раз за базовый период и начислением сложных процентов 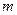раз за базовый период получим:

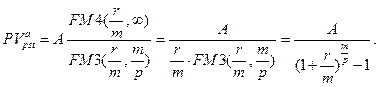(7.47)

В частности, при 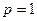из (7.47) следует, что 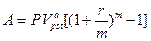, т.е. член аннуитета равен начисленным 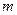раз сложным процентам на приведенную стоимость аннуите­та. При 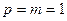формула (7.47) совпадает с (7.45).

Для определения приведенной стоимости бессрочного ан­нуитета с денежными поступлениями 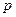раз за период и непре­рывным начислением процентов по ставке 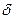перейдем к преде­лу при 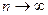в формуле (7.30). В результате получим:

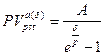(7.48)

Пример:

Фирма собирается учредить фонд для ежегодной (в конце го­да) выплаты пособий своим работникам. Определить сумму, которую фирма должна поместить на депозит в банк, чтобы обеспечить получение неограниченно долго в конце каждого года 8 тыс. тенге, если банк начисляет: а) ежегодно сложные про­центы по ставке 16%; б) ежеквартально сложные проценты по ставке 16%; в) непрерывные проценты с силой роста 16%.

Денежный поток во всех случаях является бессрочным ан­нуитетом постнумерандо, причем А = 8 тыс. тенге. Необходимо найти приведенную стоимость этого аннуитета:

а) так как 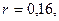то по формуле (7.45) (или по формуле
(7.47) при 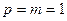) получим

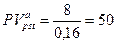тыс. тенге;

б) полагая в (7.47) 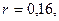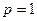, находим

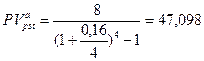тыс. тенге;

в) поскольку 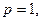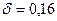, то из (7.48) следует

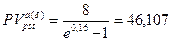тыс. тенге.

Приведенная стоимость бессрочного аннуитета пренумеран­до в общем виде определяется с помощью приведенной стоимо­сти бессрочного аннуитета постнумерандо по формуле (7.39). В частности, при 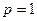,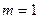из (7.39) или, что то же самое, из (7.36) следует:

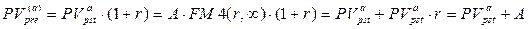
т.е. получили очевидное финансовое утверждение: приведенная стоимость бессрочного аннуитета пренумерандо отличается от таковой для постнумерандо на величину первого платежа.

Аналогичным образом выводятся формулы для оценки бессрочного аннуитета при антисипативном начислении процентов.например, из (7.28) при 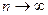получим:

(7.49)

а из (7.41):

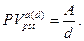(7.50)

Пример:

Определить приведенную стоимость бессрочного аннуитета с платежами в 3 тыс. тенге, выплачиваемыми в начале каждого квартала, если применяется сложная годовая учетная ставка 16%.

В данном случае имеем аннуитет пренумерандо, поэтому, полагая 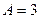, 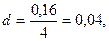по формуле (7.50) получим

тыс. руб.

Дата добавления: 2014-01-04