
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка постоянного аннуитета пренумерандо
|
|
|
|
Тема 8. ДЕНЕЖНЫЕ ПОТОКИ
1. Оценка постоянного аннуитета пренумерандо.
2. Метод депозитной книжки.
3. Бессрочный аннуитет.
4. Непрерывный аннуитет.
Если на денежные поступления начисляются только сложные проценты, то соответствующие расчетные формулы для наращенных сумм  аннуитета пренумерандо можно легко вывести из формул (7.7), (7.11), (7.12), (7.14). Поскольку денежные поступления в аннуитете пренумерандо происходят в начале каждого периода, то этот аннуитет отличается от аннуитета постнумерандо количеством периодов начисления процентов.
аннуитета пренумерандо можно легко вывести из формул (7.7), (7.11), (7.12), (7.14). Поскольку денежные поступления в аннуитете пренумерандо происходят в начале каждого периода, то этот аннуитет отличается от аннуитета постнумерандо количеством периодов начисления процентов.
Например, для срочного аннуитета пренумерандо с регулярными денежными поступлениями, равными А, и процентной ставкой  , наращенный денежный поток имеет вид
, наращенный денежный поток имеет вид

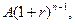 …,
…, 

следовательно, учитывая (7.7),
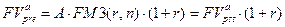 (7.31)
(7.31)
т.е. наращенная сумма (будущая стоимость) аннуитета пренумерандо больше в  раз наращенной суммы аннуитета постнумерандо.
раз наращенной суммы аннуитета постнумерандо.
Аналогичным образом для аннуитета пренумерандо с начислением процентов 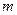 раз в течение базового периода, используя (4.11), получим:
раз в течение базового периода, используя (4.11), получим:
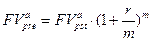 (7.32)
(7.32)
Для р -срочных аннуитетов с учетом (4.12), (4.14) можно написать следующие соотношения:
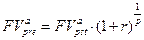 (7.33)
(7.33)
 (7.34)
(7.34)
Конечно, (7.31) - (7.33) являются частными случаями (7.34). Из формулы (7.34) следует, что  . Финансовый смысл этого неравенства очевиден: для получателя денежные поступления пренумерандо выгоднее, так как они начинаются на период раньше, чем постнумерандо, т.е. подтверждается временная ценность денег: деньги "сейчас" предпочтительнее, чем "потом".
. Финансовый смысл этого неравенства очевиден: для получателя денежные поступления пренумерандо выгоднее, так как они начинаются на период раньше, чем постнумерандо, т.е. подтверждается временная ценность денег: деньги "сейчас" предпочтительнее, чем "потом".
Несколько иной будет ситуация в р -срочном аннуитете пренумерандо, когда на взносы, поступающие в течение базового периода, начисляются простые проценты. В отличие от аннуитета постнумерандо в этом аннуитете в каждом периоде любой взнос "действует" еще  ю) часть периода, тем самым доставляя к концу периода дополнительную величину
ю) часть периода, тем самым доставляя к концу периода дополнительную величину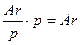 . Следовательно, к концу каждого периода взносы, число которых равно р, доставят величину
. Следовательно, к концу каждого периода взносы, число которых равно р, доставят величину 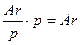 .
.
После таких рассуждений качественного характера выведем аналитически формулу для будущей стоимости  .
.
На последнее р -е поступление начисляются простые проценты за  ю) часть периода, и оно будет равно
ю) часть периода, и оно будет равно  , предпоследнее
, предпоследнее  -е поступление станет равным
-е поступление станет равным  и т.д. до первого поступления, которое станет равным
и т.д. до первого поступления, которое станет равным  . Следовательно, сумма этих величин, образующих арифметическую прогрессию, равна:
. Следовательно, сумма этих величин, образующих арифметическую прогрессию, равна:

Таким образом, используя (7.13), получим:
 (7.35)
(7.35)
С финансовой точки зрения эта формула следует из приведенных качественных рассуждений. Поскольку к концу каждого периода взносы доставляют дополнительную величину 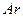 , то к будущей стоимости исходного аннуитета постнумерандо нужно прибавить еще будущую стоимость аннуитета постнумерандо с денежными поступлениями, равными
, то к будущей стоимости исходного аннуитета постнумерандо нужно прибавить еще будущую стоимость аннуитета постнумерандо с денежными поступлениями, равными 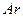 , а это и есть второе слагаемое в формуле (7.35). Естественно, и в этом случае
, а это и есть второе слагаемое в формуле (7.35). Естественно, и в этом случае  .
.
В случае начисления только сложных процентов формулы для расчетов приведенных стоимостей аннуитетов пренумерандо имеют вид, аналогичный формулам (7.31) - (7.34), т.е. находится приведенная стоимость соответствующего аннуитета постнумерандо и затем полученное значение умножается на соответствующий множитель наращения. Таким образом, рассматривая различные аннуитеты, можно написать:
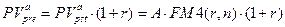 (7.36)
(7.36)
 (7.37)
(7.37)
 (7.38)
(7.38)
 (7.39)
(7.39)
Ясно, что  . Из приведенных формул понятно, почему в финансовых таблицах не уточняется, какая схема подразумевается в финансовой сделке - постнумерандо или пренумерандо; содержание финансовой таблицы инвариантно к этому фактору. Однако при применении расчетных формул или финансовых таблиц необходимо строго следить за схемой поступления денежных платежей.
. Из приведенных формул понятно, почему в финансовых таблицах не уточняется, какая схема подразумевается в финансовой сделке - постнумерандо или пренумерандо; содержание финансовой таблицы инвариантно к этому фактору. Однако при применении расчетных формул или финансовых таблиц необходимо строго следить за схемой поступления денежных платежей.
Пример:
Ежегодно в начале года в банк делается очередной взнос в размере 10 тыс. руб. Банк платит 20% годовых. Какая сумма будет на счете по истечении трех лет?
В данном случае мы имеем дело с аннуитетом пренумерандо, будущую стоимость которого и предлагается оценить. В соответствии с формулой (7.31) найдем искомую сумму S:
 тыс. руб.
тыс. руб.
Многие практические задачи могут быть решены различными способами в зависимости от того, какой денежный поток выделен аналитиком. Рассмотрим простейший пример.
Пример:
Вам предложено инвестировать 100 тыс. руб. на срок пять лет при условии возврата этой суммы частями (ежегодно по 20 тыс. тенге). По истечении пяти лет выплачивается дополнительное вознаграждение в размере 30 тыс. руб. Принимать ли это предложение, если можно "безопасно" депонировать деньги в банк из расчета 12% годовых?
Для принятия решения необходимо рассчитать и сравнить две суммы. При депонировании денег в банк к концу пятилетнего периода на счете будет сумма:
 тыс. тенге
тыс. тенге
В отношении альтернативного варианта, предусматривающего возмещение вложенной суммы частями, предполагается, что ежегодные поступления в размере 20 тыс. тенге можно немедленно пускать в оборот, получая дополнительные доходы. Если нет других альтернатив по эффективному использованию этих сумм, их можно депонировать в банк. Денежный поток в этом случае можно представить двояко:
а) как срочный аннуитет постнумерандо с 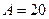 ,
, 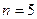 ,
, 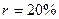 и единовременное получение суммы в 30 тыс. тенге;
и единовременное получение суммы в 30 тыс. тенге;
б) как срочный аннуитет пренумерандо с 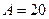 ,
,  ,
, 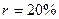 и единовременное получение сумм в 20 и 30 тыс. тенге.
и единовременное получение сумм в 20 и 30 тыс. тенге.
В первом случае на основании формулы (7.7) имеем:
 тыс. тенге.
тыс. тенге.
. Во втором случае на основании формулы (7.31) имеем:
 тыс. тенге.
тыс. тенге.
Естественно, что оба варианта привели к одинаковому ответу. Таким образом, общая сумма капитала к концу пятилетнего периода будет складываться из доходов от депонирования денег в банке (107,056 тыс. тенге), возврата доли от участия в венчурном проекте за последний год (20 тыс. тенге) и единовременного вознаграждения (30 тыс. тенге). Общая сумма составит, следовательно, 157,056 тыс. тенге. Предложение экономически нецелесообразно.
В случае антисипативного начисления процентов формулы для оценки аннуитета пренумерандо получаются таким же образом, как и приведенные ранее формулы. Величины  будут умножаться на соответствующий множитель. Например, формулы типа (7.31), (7.36) будут иметь вид:
будут умножаться на соответствующий множитель. Например, формулы типа (7.31), (7.36) будут иметь вид:
 (7.40)
(7.40)
 (7.41)
(7.41)
Если начисляются непрерывные проценты, то для получения формул определения будущей или приведенной стоимости аннуитета пренумерандо необходимо перейти к пределу при 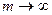 , например, в формулах (7.34), (7.39). Так, в частности, из (7.34) следует, что для непрерывных процентов
, например, в формулах (7.34), (7.39). Так, в частности, из (7.34) следует, что для непрерывных процентов
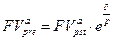 ,
,
где 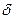 - сила роста.
- сила роста.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2440; Нарушение авторских прав?; Мы поможем в написании вашей работы!