Уравнение линии

Прямая на плоскости и в пространстве.

Изучение свойств геометрических фигур с помощью алгебры носит название аналитической геометрии, а использовать при этом мы будем так называемый метод координат.

Линия на плоскости обычно задается как множество точек, которые обладают присущими только им свойствами. Тот факт, что координаты (числа) х и у точки, лежащей на этой линии, аналитически записываются в виде некоторого уравнения.

Опр.1 Уравнением линии (уравнением кривой) на плоскости Оху называется уравнение 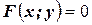(*), которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой другой точки, не лежащей на этой линии.

Из определения 1 следует, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х,у) точки этой линии и наоборот, всякому уравнению соответствует, вообще говоря, некоторая линия.

Отсюда возникают две основные задачи аналитической геометрии на плоскости.

1.Дана линия в виде множества точек. Нужно составить уравнение этой линии.

2. Дано уравнение линии. Необходимо изучить ее геометрические свойства (форму и расположение).

Пример. Лежат ли точки А (-2;1) и В (1;1) на линии 2 х + у +3=0?

Задача о нахождении точек пересечения двух линий, заданных уравнениям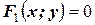и и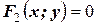, сводится к отысканию координат, которые удовлетворяют уравнению обеих линий, т.е. к решению системы из двух уравнений с двумя неизвестными.

Если эта система не имеет действительных решений, то линии не пересекаются.

Аналогично вводится понятие линии в ПСК.

Линию на плоскости можно задать двумя уравнениями

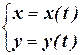, (5.1)

где х и у – произвольные координаты точки М(х;у), лежащей на данной линии, а t - переменная, называемая параметром, параметр определяет положение точки на плоскости.

Например, если 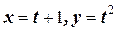, то значению параметра t=2 соответствует на плоскости точка (3;4).

Если параметр изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способом задания линии называется параметрическим, а уравнение (5.1) –параметрическим уравнением линии.

Чтобы перейти от параметрических уравнений к общему уравнению (*), надо каким – либо способом из двух уравнений исключают параметр. Однако, заметим, такой переход не всегда целесообразен и не всегда возможен.

Линию на плоскости можно задать векторным уравнением 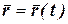, где t- скалярный переменный параметр. Каждому значению параметра соответствует определенный вектор плоскости. При изменении параметра конец вектора опишет некоторую линию.

Векторному уравнению 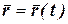в ДСК соответствуетдва скалярных уравнения

(5.1), т.е. уравнения проекций на оси координат векторного уравнения линии есть ее

параметрическое уравнения.

Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линия – траектория точки, параметр t при этом есть время.

Вывод: всякой линии на плоскости соответствует уравнение вида .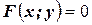

ВСЯКОМУ УРАВНЕНИЮ ВИДА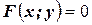соответствует в общем случае некоторая линия, свойства которой определяются данным уравнением (исключение – уравнению 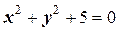на плоскости не соответствует никакой геометрический образ).

Пусть выбрана система координат на плоскости.

Опр. 5.1. Уравнением линии называется такое уравнение вида F(x;y) =0, которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней.

Уравнение вида F(x;y )=0 – называют общим уравнением линии или уравнением в неявной форме.

Таким образом, линия Г есть геометрическое место точек, удовлетворяющее данному уравнению Г={(x, y): F(x;y)=0}.

Линию называют также кривой.

Дата добавления: 2014-01-07