Уравнение прямой на плоскости

Задача 1. Найти уравнение прямой проходящей через данную точку М₀(х₀;у₀) и перпендикулярно вектору n=(A;B).

Произвольная точка М (х,у) лежит на данной прямой тогда и только тогда, когда М₀М ^ n, те М₀М × n = 0.

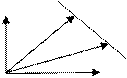Если r и r₀ радиус векторы точек М и М₀, то получаем, что

(r - r_0, n)=0 (5.2 ) –векторная форма уравнения прямой.

Или запишем скалярное произведение через координаты

A(x – x₀) + B(y- y₀)=0 (5.3) – координатная форма уравнения прямой, проходящей через точку М₀(х₀;у₀) и перпендикулярно n.

Обозначим Ах₀ + Ву₀= С, то уравнение (5.3) приводится к виду Ах + Ву +С=0 (5.4) – общее уравнение прямой, где коэффициенты А и В – определяют координаты вектора n – вектор нормали прямой.

Пусть В ¹ 0. Обозначим k= - А/В, b= - С/В, уравнение (5.4) перепишем в виде

k x + b=0 (5.5) - уравнение прямой с угловым коэффициентом.

Величина k= tg угла наклона прямой к оси ОХ, а величина b по модулю равна длине отрезка, отсекаемого прямой на оси ОУ.

у-у₀=k (x-x₀) – (5.5')- уравнение прямой с угловым коэффициентом, проходящим через заданную точку М₀(х₀;у₀).

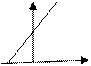
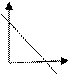k>0

k<0

k=0

Пусть С ¹ 0. Обозначим а = - А/С, b = - В/С, уравнение (5.4) перепишем в виде

x/a +y/b=1 (5.6 ) - уравнение прямой в отрезках, где а- величина отрезка отсекаемого прямой на оси ОХ, аналогично в.

Задача 2. Записать уравнение прямой, проходящей через точку М₀(х₀; у₀) с радиус вектором r₀ параллельно заданному вектору l(m;n). l – направляющий вектор прямой.

Произвольная точка М (её радиус вектор обозначим r(х;у)) лежит на данной прямой тогда и только тогда, когда r - r₀‌‌‌ ‌ l, те r - r₀=tl или r = r₀+tl (6) – параметрическое уравнение прямой в векторной форме.

Уравнение (5.6) можно записать в координатной форме.

- (5.7 ) - параметрическое уравнение прямой в координатной форме.

- (5.8) -каноническое уравнение прямой.

В частности, если прямая проходит через точки М₀(х₀;у₀) и М₁(х₁;у₁), то в качестве направляющего вектора можно взять вектор (х₁- х₀; у₁ – у₀) и уравнение (5.7) перепишем в виде

- (5.9 )- уравнение прямой проходящей через две точки М₀(х₀;у₀) и М₁(х₁;у₁).

Задача 3. Найти расстояние от прямой до точки.

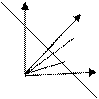При решении этой задачи используем нормальное уравнение.

Пусть дана прямая l,заданная двумя точками М и М₀ проведем через начало координат нормаль к этой прямой, где точка P пересечение прямой и нормали.

Вектор n =(cos α, sinα) – направляющими косинусами, cosβ = sin α (из прямоугольного Δ).

(r - r_0, n)=0 Þ r × n= r₀× nÞ

Поскольку r₀ n=пр_nr₀ = p - обозначим проекцию вектора r₀ на нормаль, получим

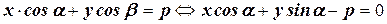(5.10) – нормальное

(нормированное) уравнение прямой, где р – перпендикуляр опущенный из начало координат на данную прямую, а угол a - угол, образованный этим перпендикуляром и осью ОХ.

Особенности данного уравнения:

1. Р- свободный член всегда отрицателен.
2. Сумма квадратов коэффициентов при неизвестных равна 1

(из свойства направляющих косинусов).

Опр. 5.2. Расстоянием от точки до прямой, называется длина перпендикуляра, опущенного из этой точки на прямую.(d)

Опр. 5.3. Отклонением точки М от прямой, называется расстояние от этой точки до прямой, взятое со знаком "+",если точка и начало координат расположены по разные стороны от прямой, и со знаком "-" -если по одну.

Одной из стандартных задач аналитической геометрии является задача вычисления отклонения точки от прямой. Эту задачу решает следующая теорема.

Теорема 5.1. Если точка М* имеет координаты (х*;у*), прямая

Задана нормальным уравнением, то отклонение точки М* от этой прямой вычисляется по формуле

d=x сosa + ysinb-p (*)

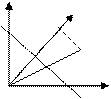Доказательство: спроектируем точку М на нормаль; пусть точка Q – её проекция. Тогда d= PQ=OQ – OP, где PQ, OQ, OP – числовые величины соответствующих векторов, расположенных по нормали, но

OQ = пр _n OM= x сosa + ysinb, OP=pÞ

d= пр _n OM – p Þ d=x сosa + ysinb-p (*) чтд.

Таким образом видим, что в правая часть данного уравнения – это левая часть нормального уравнения прямой.

Замечание. Чтобы найти расстояние от точки до прямой нужно вычислить отклонение по модулю, те в левую часть нормального уравнения (*) подставить координаты точки.

Дата добавления: 2014-01-07