Гипербола

Эллипс

Особенности уравнения окружности

1 Оно обязательно содержит квадраты переменных 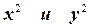с одинаковыми знаками и коэффициентами.

2 Оно не содержит члена с произведением координат xy.

По этим особенностям уравнение окружности можно отличить от других уравнений кривых II порядка.

Пример. Пусть задано уравнение .

Выяснить, какую линию II порядка оно определяет.

Определение. Эллипсом называется геометрическое место точек, сумма расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (она должна быть больше расстояния между фокусами) (рисунок 1).

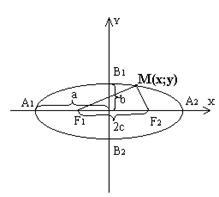рис.1

По определению эллипса имеем:

. (7.3)

Преобразуя уравнение (7.3), получим каноническое уравнение эллипса:

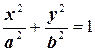, (7.4)

где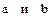- это полуоси эллипса, причем 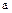откладывается на оси , а на оси 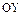.- большая ось, на которой лежат фокусы.

- малая ось эллипса.

Эллипс – симметричная кривая относительно осей координат.

Большая ось эллипса является фокальной, т.е. на этой оси расположены его фокусы, и он всегда вытянут вдоль фокальной оси.

Если большая ось эллипса , то и фокусы его на оси ординат (рисунок 2).

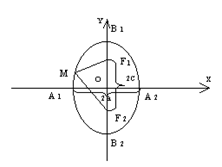
Рисунок 2

Параметры эллипса a, b и c связаны между собой. Зная два из них, можно всегда найти третий. В зависимости от фокальной оси формулы, связывающие параметры меняются. Если фокусы эллипса расположены на оси OX, то выполняется равенство (рисунок 1)

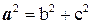
В этом случае a - самый большой параметр.

Если фокусы на оси OY (рисунок 2), то: .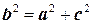

Самым большим параметром в этом случае является b.

Уравнение эллипса имеет свои особенности, по которым его можно отличать от уравнений других линий II порядка.

Оно всегда содержит сумму квадратов переменных x² и y², коэффициенты, при которых различные, в отличие от уравнения окружности. Если центр эллипса находится не в начале координат, то его уравнение имеет вид:

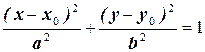, (7.5)

где - координаты центра.

Опр.7.2 Эксцентриситетом эллипса называется отношение межфокусного расстояния к

длине большей оси.

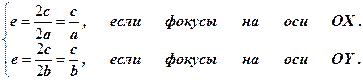
Эксцентриситет эллипса всегда положителен, но меньше 1, т.к. , т.е. .

Он характеризует форму эллипса. Чем больше эксцентриситет, тем больше вытянут эллипс вдоль фокальной оси (т.е. сжат вдоль оси OY). Если , если , то эллипс вырождается в прямую линию.

Если , то эллипс превращается в окружность.

Задача Дано уравнение эллипса 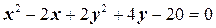. При- вести к каноническому.

Р е ш е н и е. ,

Опр. 7.3 Гиперболой называется геометрическое место точек, разность расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (она должна быть положительной и меньше расстояния между фокусами) .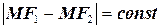

Рисунок 3

Если обозначить постоянную величину 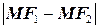через 2 а, а расстояние между фокусами через 2 с и выбрать систему так, чтобы ось OX совпала с фокальной осью , а ось ординат проходила бы через середину отрезка , тогда каноническое уравнение гиперболы примет вид:

, (7.6)

где а и b - полуоси гиперболы; а расположена на оси ОХ, а b по оси OY (рисунок 4).

Ось, на которой расположены фокусы гиперболы, называется действительной, на ней расположены вершины гиперболы – т. А₁ и А₂. В этих точках гипербола пересекает действительную ось А₁ (-а;0), А₂ (а;0).

Вторая ось гиперболы, с которой она не имеет общих точек, называется мнимой осью.

А₁А₂=2а; F₁F₂=2c; F₁ (-c;0); F₂ (c;0).

Рисунок 4

Если фокусы гиперболы расположены на оси OY, то уравнение гиперболы имеет вид:

. (7.7)

В этом случае действительной осью, на которой лежат вершины гиперболы и фокусы, является , - мнимая ось, - межфокусное расстояние. Координаты фокусов будут: . Из уравнений (7.6) и (7.7) видно, что фокальная (действительная) ось гиперболы та, которая со знаком "+".

Числовое значение самой оси роли не играет, в отличие от эллипса.

Связь между параметрами у гиперболы постоянная, т.е. не зависит от фокальной оси. Межфокусное расстояние является самым большим параметром

.

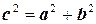Опр. 7.4 Эксцентриситетом гиперболы называется отношение межфокусного

расстояния к длине действительной оси.

, если фокальная ось OX.

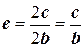, если фокусы на оси OY.

Эксцентриситет гиперболы всегда положителен и больше 1, так как c>a и c>b, т.е. 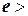1.

Большую роль у гиперболы играют асимптоты, так как они направляют ветви гиперболы.

Уравнения асимптот не зависят от фокальной оси и имеют вид

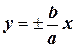. (7.8)

Построение гиперболы начинают с асимптот. Если построить прямоугольник со сторонами, параллельными координатным осям и равными 2 а и 2b, то его диагонали будут асимптотами гиперболы (рисунки 3, 4).

Если гипербола смещена в системе координат, то ее каноническое уравнение имеет вид

, (7.9)

где - координаты центра гиперболы.

Дата добавления: 2014-01-07