
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие базиса
|
|
|
|
Линейная зависимость и независимость векторов.
Линейные операции над векторами, то есть сумма векторов и умножение вектора на число, позволяют составить линейную комбинацию векторов 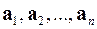 с числами
с числами 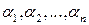 , которая дает некоторый вектор
, которая дает некоторый вектор 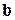 :
:
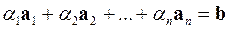
Задача 1. Векторы а, 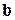 ,
, 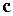 коллинеарны и имеют одинаковое направление, причем
коллинеарны и имеют одинаковое направление, причем 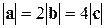 . Что можно сказать о векторах
. Что можно сказать о векторах
1) 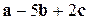 , 2)
, 2) 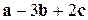 , 3)
, 3) 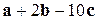 ?
?
Решение. 1) Из условия задачи и из определения произведения вектора на число следует, что 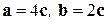 . Тогда искомый вектор равен
. Тогда искомый вектор равен
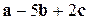 =
= 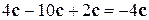
Он коллинеарен данным векторам и противоположно направлен, длина его совпадает с длиной вектора 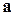 . Случаи 2,3 рассмотреть самостоятельно. ¨
. Случаи 2,3 рассмотреть самостоятельно. ¨
Векторы 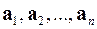 линейно зависимы, если существуют такие числа
линейно зависимы, если существуют такие числа 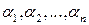 , не все одновременно равные нулю (то есть числа, для которых выполняется условие
, не все одновременно равные нулю (то есть числа, для которых выполняется условие 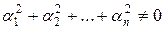 ), что линейная комбинация данных векторов с этими числами дает нулевой вектор:
), что линейная комбинация данных векторов с этими числами дает нулевой вектор:
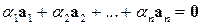 . (1.1)
. (1.1)
Например, векторы а,  ,
,  задачи 1 линейно зависимы, так как существуют такие числа
задачи 1 линейно зависимы, так как существуют такие числа 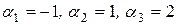 ,
, 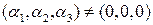 , с которыми линейная комбинация
, с которыми линейная комбинация 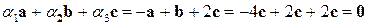 .
.
Для этих векторов можно указать и другие ненулевые наборы чисел, например,  (проверьте!), с которыми удовлетворяется условие (1.1).
(проверьте!), с которыми удовлетворяется условие (1.1).
Векторы 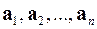 линейно независимы, если условие (1.1) выполняется только с равными нулю числами
линейно независимы, если условие (1.1) выполняется только с равными нулю числами 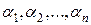 . Например, векторы
. Например, векторы 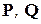 задачи 1 предыдущего раздела линейно независимы, так как диагональ параллелограмма, построенного на "растянутых" векторах
задачи 1 предыдущего раздела линейно независимы, так как диагональ параллелограмма, построенного на "растянутых" векторах 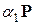 и
и 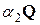 , может равняться нулю лишь тогда, когда
, может равняться нулю лишь тогда, когда 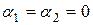 .
.
Для двух векторов 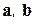 необходимым и достаточным условием линейной зависимости является их коллинеарность. Для трех векторов необходимое и достаточное условие линейной зависимости – их компланарность. Произвольные четыре вектора всегда линейно зависимы.
необходимым и достаточным условием линейной зависимости является их коллинеарность. Для трех векторов необходимое и достаточное условие линейной зависимости – их компланарность. Произвольные четыре вектора всегда линейно зависимы.
Три линейно независимых вектора 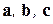 образуют в пространстве базис, если любой вектор
образуют в пространстве базис, если любой вектор 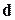 можно представить в виде:
можно представить в виде:
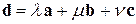 . (1.2)
. (1.2)
Равенство (1.2) называют разложением вектора 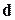 по базису
по базису 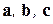 , а числа
, а числа 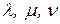 - координатами вектора
- координатами вектора 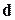 в этом базисе.
в этом базисе.
Для базисных векторов 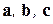 равенство (1.2) принимает вид:
равенство (1.2) принимает вид:
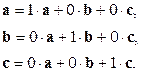
Координаты каждого вектора в заданном базисе определяются однозначно. Если вектор 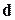 равен нулю, то в разложении (1.2) все три числа
равен нулю, то в разложении (1.2) все три числа 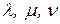 равны нулю.
равны нулю.
Базис в пространстве образует произвольная тройка некомпланарных векторов, базис на плоскости - произвольная пара неколлинеарных векторов, базис на прямой - произвольный ненулевой вектор.
Задача 2. Постройте разложение заданного вектора 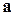 на два компланарных с ним слагаемых, если известны
на два компланарных с ним слагаемых, если известны
1) направления каждого слагаемого,
2) направление и длина одного из слагаемых ¨
Если базисные векторы 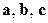 привести к общему началу в точке
привести к общему началу в точке 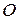 , то координаты вектора
, то координаты вектора 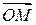 в базисе
в базисе 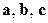 называют аффинными координатами точки
называют аффинными координатами точки 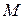 . Частный случай аффинных координат – декартовы (прямоугольные) координаты. В декартовой системе координат базисные векторы обозначаются
. Частный случай аффинных координат – декартовы (прямоугольные) координаты. В декартовой системе координат базисные векторы обозначаются 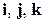 , они единичны и взаимно перпендикулярны (ортогональны). Направление ортов
, они единичны и взаимно перпендикулярны (ортогональны). Направление ортов 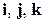 совпадает с направлением координатных осей
совпадает с направлением координатных осей 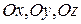 соответственно. Декартовы координаты
соответственно. Декартовы координаты 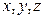 точки
точки 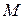 - это координаты радиуса-вектора точки
- это координаты радиуса-вектора точки 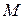 (координаты вектора
(координаты вектора 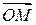 ) в базисе
) в базисе 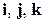 .
.
Декартовы координаты вектора а обозначим 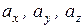 ,они равны проекциям этого вектора на координатные оси
,они равны проекциям этого вектора на координатные оси 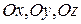 соответственно. Значит,
соответственно. Значит, 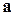 =
= 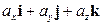 или
или 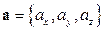 .
.
Длина (модуль) вектора 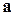 определяется формулой
определяется формулой
 . (1.3)
. (1.3)
Определим проекцию вектора а на ось 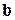 соотношением
соотношением
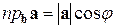 (1.4)
(1.4)
Здесь 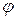 - угол между вектором а и осью
- угол между вектором а и осью 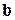 ,
, 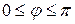 . Заметим, что
. Заметим, что 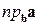 – число.
– число.
Проекция вектора на ось имеет линейные свойства, а именно:
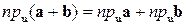 ,
, 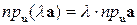
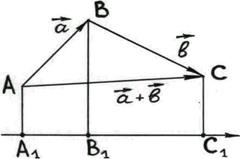 Линейные свойства проекции вектора на ось может объяснить рис.5, где
Линейные свойства проекции вектора на ось может объяснить рис.5, где
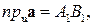
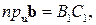
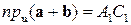 , значит,
, значит, 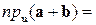
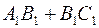
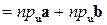
Рис.5
Если ввести 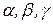 - углы наклона вектора а к осям
- углы наклона вектора а к осям 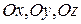 соответственно, то получим
соответственно, то получим
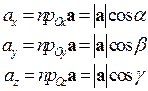 , (1.5)
, (1.5)
Числа 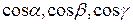 называют направляющими косинусами вектора а. Из формул (1.3) и (1.5) следует, что
называют направляющими косинусами вектора а. Из формул (1.3) и (1.5) следует, что
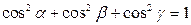
Например, вектор а с координатными осями может образовывать углы 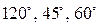 , так как
, так как 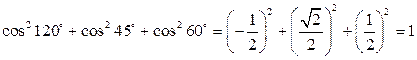 .
.
Задача 3. Проверьте, может ли некоторый вектор 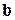 образовывать с координатными осями углы
образовывать с координатными осями углы 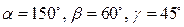 .
.
Ответ. Не может. ¨
Если ненулевой вектор а разделить на его модуль, получим орт а° вектора а:
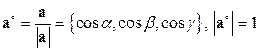 . (1.6)
. (1.6)
В силу линейности проекции при сложении векторов их соответствующие координаты складываются, при умножении вектора на число каждая его координата множится на это число.
Если в системе координат 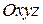 заданы две точки
заданы две точки  и
и 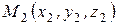 , то вектор
, то вектор 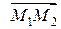 имеет координаты
имеет координаты
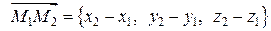 (1.7)
(1.7)
Задача 4. В треугольнике 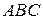 известны одна из вершин
известны одна из вершин  и векторы
и векторы 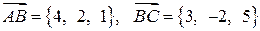 . Найти координаты двух других вершин и координаты вектора
. Найти координаты двух других вершин и координаты вектора 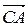 .
.
Решение. Обозначим координаты точек 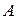 и
и 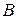 через
через 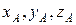 и
и 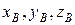 соответственно.
соответственно.  По формуле (1.7)
По формуле (1.7) 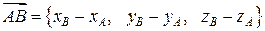 .
.
Итак, имеем вектор 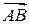 и координаты его начала
и координаты его начала 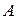 , что позволяет определить координаты конца
, что позволяет определить координаты конца 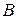 :
:
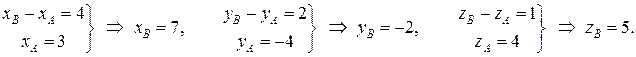
Получили 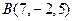 . Аналогично находим координаты точки
. Аналогично находим координаты точки 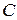 :
:
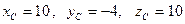 .
.
Остается найти вектор 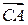 :
:
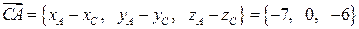 ♦
♦
Длина вектора  равна расстоянию
равна расстоянию 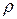 между точками
между точками 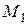 и
и 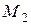 :
:
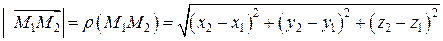 . (1.8)
. (1.8)
Задача 5. Можно ли вписать окружность в четырехугольник с вершинами в точках 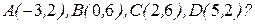
Решение. Напомним, что окружность можно вписать в четырехугольник тогда и только тогда, когда суммы длин противоположных сторон четырехугольника равны между собой. Вычислим
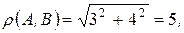
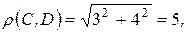
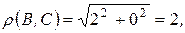
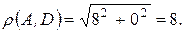
Получили 2+8=5+5, значит, в данный четырехугольник окружность вписать можно ¨
Задача 6. Даны векторы  . Найти координаты векторов
. Найти координаты векторов 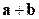 и
и 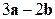 . Определить длину вектора
. Определить длину вектора 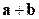 его орт.
его орт.
Решение. Координаты вектора 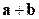 - это суммы соответствующих координат векторов а и
- это суммы соответствующих координат векторов а и 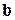 , то есть
, то есть 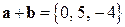 . Модуль вектора
. Модуль вектора 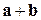 найдем по формуле (1.3):
найдем по формуле (1.3): 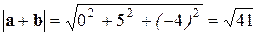 . Осталось в соответствии с(1.6) найти орт вектора
. Осталось в соответствии с(1.6) найти орт вектора 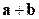 :
:
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 811; Нарушение авторских прав?; Мы поможем в написании вашей работы!