
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторное произведение
|
|
|
|
Задачи
- Вычислить угол между векторами
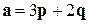 и
и 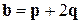 , где
, где 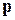 и
и 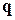 – единичные взаимно перпендикулярные векторы.
– единичные взаимно перпендикулярные векторы. - Векторы
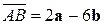 ,
, 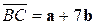 и
и 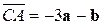 , где
, где 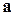 и
и 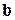 – взаимно перпендикулярные орты, образуют треугольник. Определить углы этого треугольника.
– взаимно перпендикулярные орты, образуют треугольник. Определить углы этого треугольника. - Вычислить скалярное произведение векторов
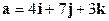 и
и 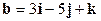 .
. - Найти единичный вектор
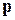 , одновременно перпендикулярный к оси абсцисс и к вектору
, одновременно перпендикулярный к оси абсцисс и к вектору 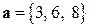 .
. - Убедиться, что треугольник с вершинами
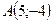 ,
, 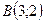 ,
, 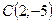 прямоугольный.
прямоугольный. - В плоскости
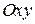 найти вектор
найти вектор 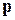 , перпендикулярный вектору
, перпендикулярный вектору 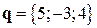 и имеющий одинаковую с ним длину.
и имеющий одинаковую с ним длину. - Даны векторы
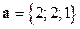 ,
, 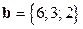 . Найти
. Найти 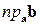 ,
, 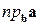 .
. - Доказать, что вектор
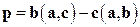 перпендикулярен вектору
перпендикулярен вектору 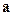 .
. - Даны векторы
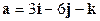 ,
, 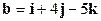 ,
, 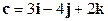 . Вычислить
. Вычислить 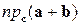 .
. - Вычислить
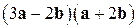 и
и 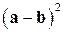 , если
, если  ,
, 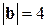 ,
, 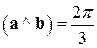 .
. - Параллелограмм построен на векторах
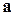 и
и 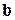 . Найти угол между его диагоналями и длины диагоналей, если
. Найти угол между его диагоналями и длины диагоналей, если
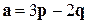 ,
, 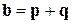 ,
,  ,
, 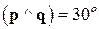 .
.
- Найти угол между векторами
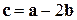 и
и 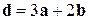 , если
, если  ,
, 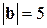 и угол между векторами
и угол между векторами 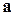 и
и 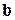 равен 120°.
равен 120°. - Найти угол между векторами
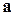 и
и 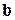 , если они имеют одинаковую длину, а векторы
, если они имеют одинаковую длину, а векторы 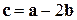 и
и 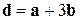 ортогональны.
ортогональны. - Найти работу
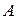 силы
силы 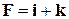 при перемещении материальной точки из начала в конец вектора
при перемещении материальной точки из начала в конец вектора 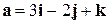 .
. - При каких значениях
 и
и  векторы
векторы 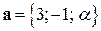 и
и 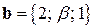 перпендикулярны, если
перпендикулярны, если  ?
?
Тройку некомпланарных векторов 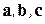 называем правой, если после сведения к общему началу эти векторы упорядочены, как большой, указательный и средний пальцы правой руки. Если векторы
называем правой, если после сведения к общему началу эти векторы упорядочены, как большой, указательный и средний пальцы правой руки. Если векторы 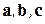 после сведения к общему началу упорядочены, как эти же пальцы левой руки, то тройку векторов называем левой. Всего из трех векторов
после сведения к общему началу упорядочены, как эти же пальцы левой руки, то тройку векторов называем левой. Всего из трех векторов 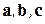 можно составить шесть различных троек. Тройки
можно составить шесть различных троек. Тройки 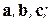
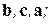
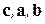 имеют одинаковую ориентацию. Если они, например, правые, то тройки
имеют одинаковую ориентацию. Если они, например, правые, то тройки 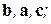
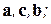
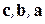 –левые, т.е. ориентированы противоположно.
–левые, т.е. ориентированы противоположно.
Система координат называется правой или левой в зависимости от того, правой или левой является тройка базисных векторов. Привычная для нас декартова система координат - правая.
Векторным произведением векторов 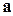 и
и 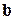 называем вектор
называем вектор 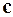 , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1) вектор 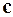 ортогонален каждому из векторов
ортогонален каждому из векторов 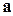 и
и 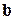 (то есть ортогонален плоскости, в которой находятся векторы
(то есть ортогонален плоскости, в которой находятся векторы 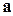 и
и 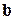 ),
),
2) 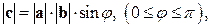
3) вектор 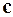 направлен так, что тройка
направлен так, что тройка 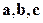 правая.
правая.
Здесь 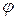 - угол между векторами
- угол между векторами 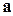 ,
, 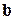 . Операцию векторного произведения обозначаем символом
. Операцию векторного произведения обозначаем символом 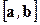 (или
(или 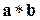 ). Например, для ортов
). Например, для ортов 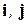 имеем по определению (проверьте!)
имеем по определению (проверьте!) 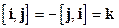 . Результаты векторного умножения для всех вариантов пар базисной тройки
. Результаты векторного умножения для всех вариантов пар базисной тройки 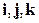 приведены в таблице:
приведены в таблице:
| 
| 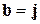
| 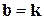
|
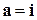
| 
| 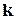
| - 
|
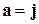
| - 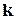
| 
| 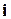
|
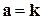
| 
| - 
| 
|
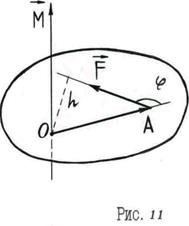 Понятие векторного произведения происходит из механики. Действительно, пусть на тело, закрепленное в точке
Понятие векторного произведения происходит из механики. Действительно, пусть на тело, закрепленное в точке 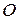 , действует сила
, действует сила 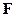 , приложенная в точке
, приложенная в точке 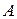 (рис.11). Под действием силы тело вращается вокруг оси, перпендикулярной к плоскости, в которой находятся векторы
(рис.11). Под действием силы тело вращается вокруг оси, перпендикулярной к плоскости, в которой находятся векторы 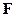 и
и 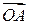 . Величина момента
. Величина момента 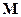 силы
силы 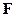 относительно точки
относительно точки 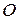 равняется произведению модуля силы
равняется произведению модуля силы 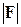 на плечо
на плечо 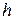 (расстояние от точки
(расстояние от точки 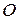 до линии действия силы
до линии действия силы 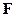 ):
): 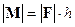 . Если сила
. Если сила 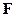 образует с вектором
образует с вектором 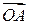 угол
угол 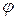 , то
, то 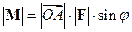 , т.к.
, т.к. 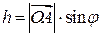 . Вектор
. Вектор 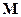 направлен по оси вращения так, что из его конца видим вращение против часовой стрелки, то есть тройка
направлен по оси вращения так, что из его конца видим вращение против часовой стрелки, то есть тройка 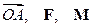 - правая. Поэтому
- правая. Поэтому
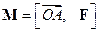 . ( 1.20)
. ( 1.20)
Геометрические свойства векторного произведения:
1) Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
2) Модуль векторного произведения равен площади параллелограмма, построенного на приведенных к обще- Рис.12 му началу векторах 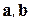 :
:
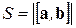 (1.21)
(1.21)
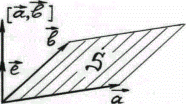 Введём орт
Введём орт 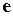 векторного произведения
векторного произведения 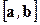 (рис.12). Из (1.21) получаем:
(рис.12). Из (1.21) получаем:
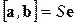 (1.22)
(1.22)
Алгебраические свойства векторного произведения:
1) 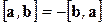 ,
,
2) 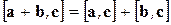 ,
,
3) 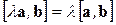 ,
,
4) 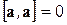 для
для 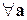 .
.
Обращаем внимание на то, что векторное произведение антикоммутативно (в отличие от скалярного произведения).
Пусть заданы декартовы координаты векторов 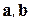 :
:
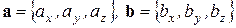 .
.
Векторное произведение 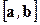 можно вычислить по формуле (попробуйте это доказать самостоятельно, опираясь на определение и свойства векторного произведения, а также на материал раздела (1.6)):
можно вычислить по формуле (попробуйте это доказать самостоятельно, опираясь на определение и свойства векторного произведения, а также на материал раздела (1.6)):
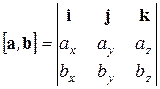 (1.23)
(1.23)
Раскрывая определитель в формуле (1.23) по элементам первой строки, получаем разложение вектора 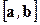 по базису
по базису  :
:
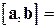
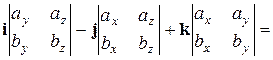
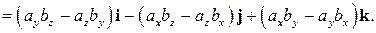
Критерий колллинеарности векторов 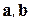 (то есть равенство нулю всех координат вектора
(то есть равенство нулю всех координат вектора 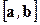 ) приводит к знакомому признаку (1.9).
) приводит к знакомому признаку (1.9).
Задача 1. Вычислить 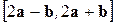 , если
, если 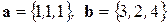 .
.
Решение. С учетом алгебраических свойств векторного произведения получаем: 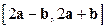 =
= 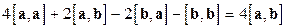 , так как
, так как 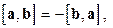
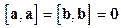 . По формуле (1.23) находим
. По формуле (1.23) находим
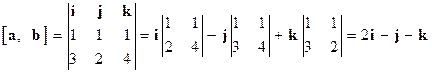 .
.
Итак, 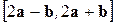 =
= 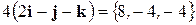 . ¨
. ¨
Задача 2. Сила 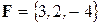 приложена к точке
приложена к точке 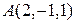 . Вычислить момент
. Вычислить момент 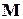 этой силы относительно начала координат.
этой силы относительно начала координат.
Решение. Момент силы 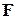 относительно точки
относительно точки 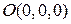 найдем по формуле (1.20):
найдем по формуле (1.20): 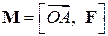 , где
, где 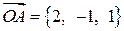 .
.
Осталось подставить координаты векторов 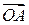 и
и 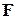 в формулу (1.23):
в формулу (1.23):
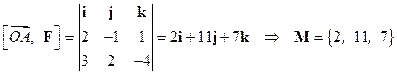 . ¨
. ¨
Задача 3. Сила 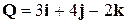 приложена к точке
приложена к точке 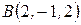 . Определить величину и направляющие косинусы момента этой силы относительно начала координат.
. Определить величину и направляющие косинусы момента этой силы относительно начала координат.
Ответ. 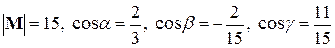 . ¨
. ¨
Задача 4. Три силы 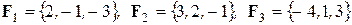 приложены к точке
приложены к точке 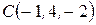 . Определить величину и направляющие косинусы момента равнодействующей
. Определить величину и направляющие косинусы момента равнодействующей 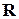 этих сил относительно точки
этих сил относительно точки 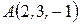 .
.
Решение. Найдем равнодействующую 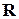 данных сил:
данных сил:
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 944; Нарушение авторских прав?; Мы поможем в написании вашей работы!