Скалярное произведение

Задачи

.

.

Вектор 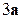имеет координаты 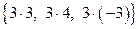= 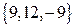, вектор 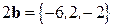, тогда вектор 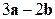={15,10,-7} ¨

Признаком коллинеарности векторов 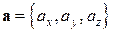и 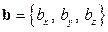является пропорциональность их координат:

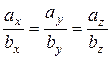(1.9)

Задача 7. Показать, что векторы 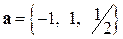и 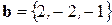линейно зависимы.

Решение. Векторы 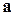и 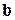имеют пропорциональные координаты: 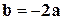, значит, они коллинеарны по признаку (1.9). А коллинеарность векторов является достаточным условием их линейной зависимости ¨

Задача 8. Заданы точки

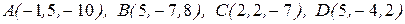
Доказать, что векторы 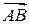и коллинеарны.

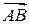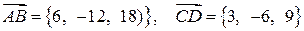Решение. Найдем сначала координаты векторов и по формуле (1.7): . Проверим их коллинеарность по признаку (1.9): 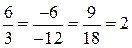. Значит, векторы 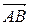и коллинеарны, . ¨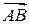

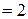
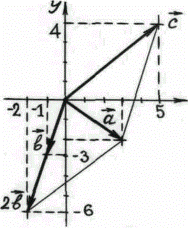
Задача 9. На плоскости заданы векторы 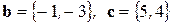. Найти разложение вектора 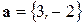по базису .

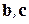Решение. Сначала проверим, могут ли векторы 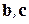образовывать базис. Координаты этих векторовнепропорциональны: 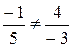, то есть эта пара неколлинеарных векторов образует базис на плоскости.

По условию, разложение заданных векторов в декартовом базисе 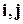имеет вид

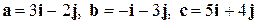. Рис.6

Запишем разложение вектора 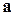по базису : .

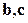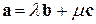Здесь числа 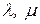- неизвестные координаты вектора 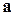в базисе 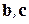. Подставим в это разложение декартовы представления векторов :

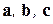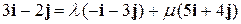
и сгруппируем относительно :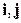

Поскольку координаты вектора в данном базисе определяются однозначно, из равенства двух векторов следует равенство соответствующих координат:

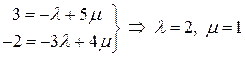
Рекомендуем решить эту систему по формулам Крамера (см. раздел 1.6 ).

Получили разложение вектора 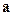по базису 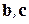: 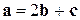(рис. 6). ¨

Задача 10. На плоскости заданы векторы 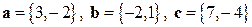. Определить разложение каждого из них, принимая за базис два другие.

Ответ: . ¨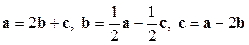

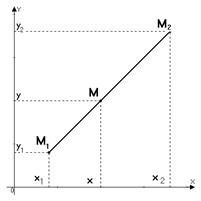
Точка 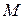делит отрезок в отношении 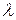, если 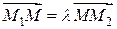. Из рис. 7 следует:

.

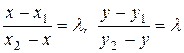Отсюда получаем формулы деления отрезка в заданном отношении ,: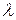

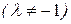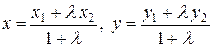. (1.10) Рис.7

Если в (1.10) положить 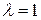, получим формулы для определения координат середины отрезка:

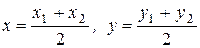. (1.11)

С помощью формул (1.10) можно найти центр масс системы материальных точек, предполагая, что центр масс двух точек 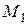и 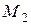с массами соответственно 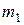и 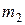находится на отрезке и делит его в отношении 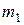: 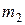. Значит, по формулам(1.10) при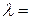 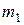: 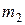получаем координаты центра масс 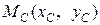двух материальных точек:

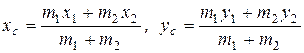. (1.12)

При необходимости прибавляется третья координата .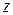

Задача 11. В точках 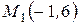и 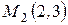сосредоточенны массы 50 кг и100 кг. Определить центр масс системы.

Решение. По формулам (1.12):

.¨

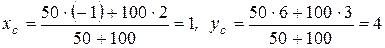Координаты центра масс системы 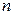точек 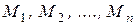с массами соответственно 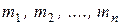вычисляются по формулам:

.

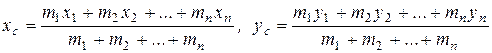Задача 12. Однородная плита имеет форму квадрата со стороной 12. В плите сделан квадратный вырез, прямые разреза проходят через центр квадрата, координатные оси направлены по ребрам плиты (рис. 8). Определить координаты центра масс плиты.

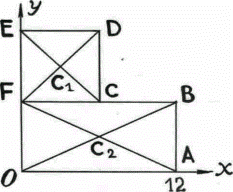Решение. Разрежем плиту по линии 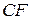и найдем центры квадрата 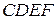и прямоугольника 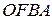, они находятся на пересечении диагоналей этих фигур в точках 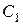и . Запишем координаты вершин:

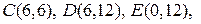
Рис.8

Точка 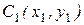делит диагонали квадрата пополам. По формулам (1.11) находим .

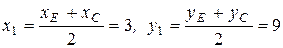Для точки 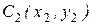получаем .

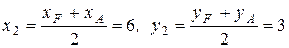Масса 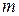однородной плиты пропорциональна площади плиты и равна , где 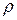- плотность, 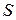- площадь. Значит, в точке 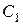сосредоточена масса 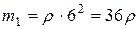, а в точке - масса 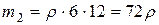. Центр масс плиты найдем по формулам (1.12):

¨

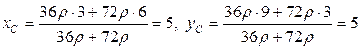1. Даны вершины треугольника: 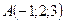, , 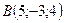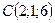. Разложить векторы, совпадающие с его сторонами, по основным ортам .
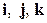2. Найти длину вектора 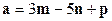, если

; , .

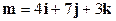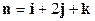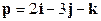1. Найти единичный вектор 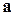, параллельный вектору .
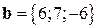2. Зная, что векторы 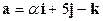и 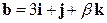коллинеарны, определить коэффициенты 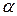и .
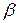3. Найти длину вектора 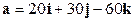и его направляющие косинусы.
4. Доказать, что 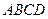- параллелограмм, если

, , .

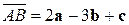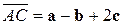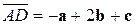1. Может ли некоторый ненулевой вектор образовывать с векторами 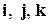углы, равные соответственно а) 120°, 135°,45°; б)120°, 135°, 60°?
2. Найти значения параметра 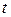, при которых вектор 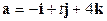имеет длину, равную 5, и образует с вектором 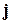тупой угол.
3. При каких значениях параметра 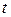вектор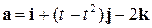

а) образует с вектором 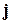угол 90°; б) коллинеарен вектору .

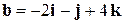1. Даны векторы 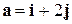, , 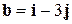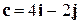. Определить разложение каждого из них, принимая за базис два другие
2. Даны вершины треугольника: 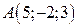, , 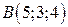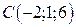. Записать векторы, идущие из вершин по медианам треугольника.

Дата добавления: 2014-11-06