Преобразование декартовых координат на плоскости

.

В круглых скобках мы видим раскрытые по правилу (1.27) определители второго порядка, значит, можем записать

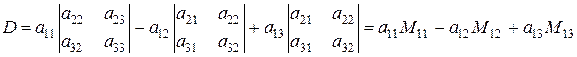.(1.32)

Здесь обозначено 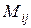– минор элемента 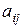– это определитель, который получается из определителя 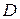после вычеркивания 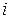-ой строки и 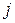-го столбца. Формула (1.32) – разложение определителя по элементам первой строки. Аналогично можно получить разложение определителя по элементам любой другой строки (столбца).

Задача 7. Вычислить определитель задачи 5, разлагая его

1) по первой строке, 2)по второму столбцу.

Решение.

1)

.

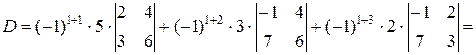
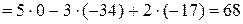2) ¨

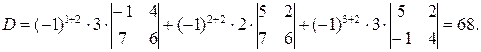Для системы трех линейных уравнений с тремя неизвестными

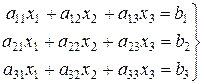
формулы Крамера приобретают вид 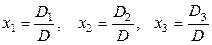. Здесь

, , .

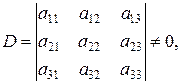
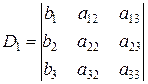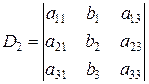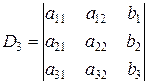Задача 8. Решить систему трех линейных уравнений с тремя неизвестными

.

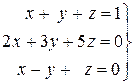Ответ. . ¨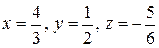

При параллельном переносе системы координат 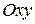вдоль вектора 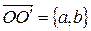получаем новую систему 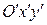, где

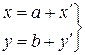. (1.33)

Здесь 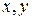– координаты точки 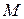относительно старой системы координат, 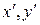– координаты той же точки относительно новой системы, 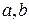– координаты нового начала 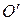относительно старой системы.

Задача 1. Даны точки 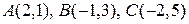. Найти их координаты в новой системе, если начало координат перенесено в точку .

Решение. Согласно (1.33) запишем:

.

Следовательно, для точки 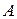получаем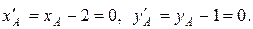

Координаты точек 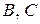в новой системе найдите самостоятельно.

Ответ. ¨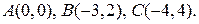

Задача 2. Дана функция 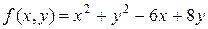. Найти выражение 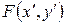этой функции в новой системе координат, если начало координат перенесено в точку .

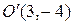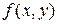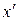Решение. Подставим в функцию вместо и их выражения через новые координаты и 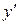: 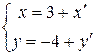. Получим

.

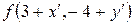
В новой системе координат функция принимает вид

.

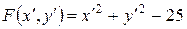Вид функции упростился за счет отсутствия членов с первыми степенями новых переменных 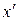и . ¨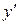

Задача 3. Найти точку, при перенесении в которую начала координат выражение для функции 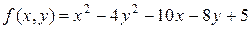не содержало бы членов первой степени относительно новых переменных.

Ответ. Начало координат нужно перенести в точку .¨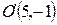

При повороте системы координат 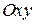на угол 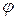(против часовой стрелки) старые координаты 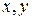произвольной точки 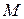связаны с новыми ее координатами 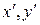соотношениями:

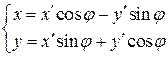1.34)

Задача 4. Систему координат повернули на угол 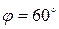. В новой системе известны координаты точки 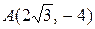. Определить координаты этой точки в старой системе.

Решение. Согласно (1.32) вычислим

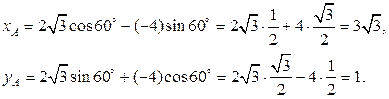
Следовательно, в старой системе . ¨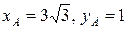

Задача 5. Дана функция 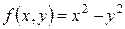. Координатные оси повернули на угол 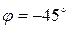. Найти выражение для этой функции в новой системе координат.

Решение. Согласно (1.34) находим:

.

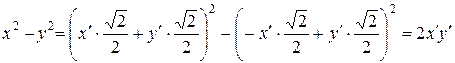В новой системе координат заданная функция вместо квадратов переменных содержит лишь их произведение. ¨

Задача 6. Доказать, что выражение функции не изменяется при повороте координатных осей на произвольный угол . ¨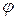

Задача 7. На какой угол нужно повернуть координатные оси, чтобы выражение функции 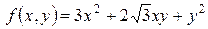после преобразования не содержало члена с произведением новых переменных?

Решение. Преобразуем выражение данной функции в соответствии с (1.34):

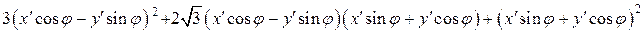Коэффициент при произведении 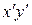должен равняться нулю:

.

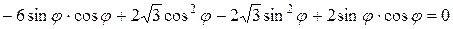После элементарных преобразований получаем уравнение

,

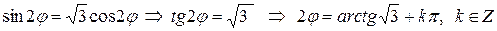или 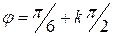. Этому условию удовлетворяют углы

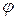=30°, 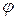=120°; 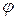=-60°; 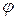=150°;… ¨

Одну из двух произвольных (правых) декартовых систем координат можно получить из другой путем параллельного переноса на вектор 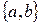и последующего поворота на угол 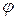(против часовой стрелки):

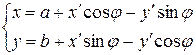(1.35)

Задача 8. Координаты точек 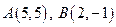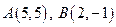определены в новой системе координат. Вычислить координаты этих точек в старой системе, если начало координат перенесено в точку 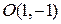, а координатные оси повернули на острый угол .

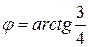Решение. Найдем сначала :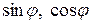

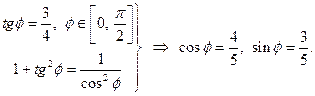
Теперь по формулам (1.35) для старых координат точки 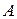получаем:

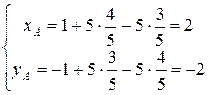
Старые координаты точки 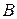определите самостоятельно. ¨

Дата добавления: 2014-11-06