Системы линейных уравнений. В этом разделе приведем вспомогательный материал из линейной алгебры, содержащий краткие сведения об определителях второго и третьего порядков

В этом разделе приведем вспомогательный материал из линейной алгебры, содержащий краткие сведения об определителях второго и третьего порядков. Излагается также метод решения систем двух (трех) линейных уравнений с двумя (тремя) неизвестными. Этот материал существенно используется как в предыдущих, так и в последующих разделах.

Прямоугольную таблицу чисел

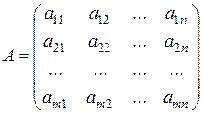
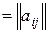
называем 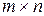матрицей. Здесь – число строк, – число столбцов, 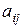– элемент матрицы, который находится в 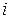-ой строке и 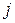-ом столбце.

Если 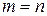, то матрица называется квадратной, – ее порядок.

Квадратной матрице 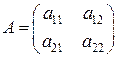второго порядка ставится в соответствие определитель (детерминант), который будем обозначать одним из символов 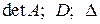и вычислять по правилу

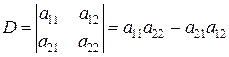(1.27)

Задача 1. Вычислить определители

.

Решение. По формуле (1. 27) находим:

,

. ¨

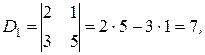
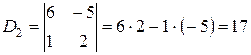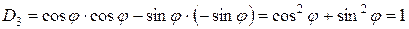Задача 2. Решить уравнение

1) , 2) .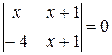

Ответ. 1) 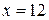, 2) . ¨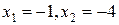

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

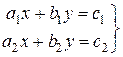(1.28)

Исключим неизвестную , для чего умножим первое уравнение системы на 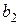, второе на 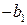, а затем сложим преобразованные равенства. Получим

.

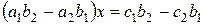Теперь исключим неизвестную , для чего умножим первое уравнение на 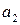, а второе на 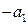. После сложения получим:

.

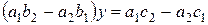Введем обозначения .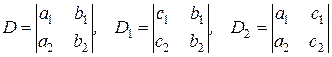

С учетом этих обозначений (1.28) превращается в эквивалентную систему:

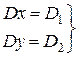. (1.29)

Определитель , составленный из коэффициентов при неизвестных, называют определителем системы, определители получаются из определителя заменой первого (второго) столбца столбцом из свободных членов системы.

Если 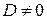, то система (1.29), а вместе с ней и исходная система (1.28) имеет единственное решение, которое находим по формулам Крамера:

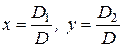. (1.30)

Если 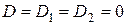, то система (1.29) имеет множество решений (не определена). Еслиже 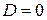, а, по крайней мере, один из определителе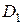й или 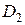отличен от нуля, то система не имеет ни одного решения (несовместна).

Этот результат имеет простую геометрическую интерпретацию. Рассмотрим две прямые 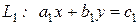и 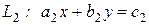. Если эти прямые пересекаются в одной точке, то система (1.28) имеет единственное решение. Если прямые сливаются в одну, то система имеет множество решений. Наконец, если прямые параллельны, система не имеет ни одного решения (см. часть 2 "Линейные образы"). ¨

Задача 3. Решить систему .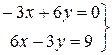

Решение. Вычислим определитель системы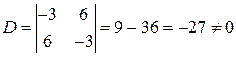

и определители : .

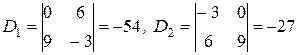По формулам Крамера находим . ¨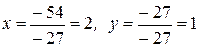

Задача 4. Исследовать, при каких значениях параметра 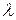система

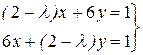
а) определена, б) не определена, в) несовместна.

Решение. Вычислим определитель системы:

.

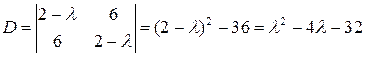Уравнение 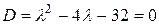имеет два корня: 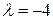и 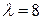. Вычислим

.

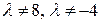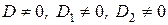Следовательно, когда , то система определена. Ее единственное решение находим по формулам Крамера:

.

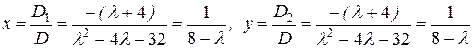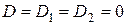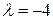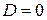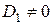Когда , то есть когда , система не определена (имеет множество решений). Наконец, когда , а или 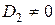, то есть при 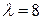, система несовместна. ¨

Квадратной матрице третьего порядка 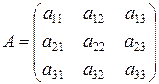ставится в соответствие определитель третьего порядка:

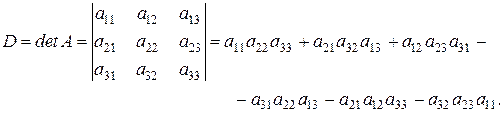(1.31)

Конструкцию слагаемых и их знаки легко запомнить с помощью простой схемы

(правило треугольника):

Со знаком "+" Со знаком "-"

Задача 5. Вычислить определитель 3-го порядка .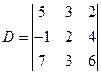

Решение. По правилу треугольника находим:

¨

Задача 6. Показать, что . ¨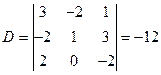

Решение. Перегруппируем слагаемые в выражении (1.31), выделяя, например, элементы 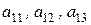первой строки:

Дата добавления: 2014-11-06