Определители второго и третьего порядка

Задачи

.

Смешанным(векторно-скалярным) произведением трех векторов называем произведение,где векторы и множатся векторно, а полученный вектор множится скалярно на вектор. Смешанное произведение - скалярная величина.

Двойное векторное произведение.

Например, .

Заметим, что смешанное произведение векторов, два из которых совпадают, равно нулю. В самом деле, если , то 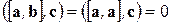, потому что векторный квадрат 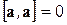. Если 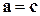, то вектор 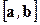по определению векторного произведения перпендикулярен к вектору 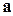, а скалярное произведение такого вектора на вектор 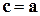равно нулю: .

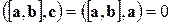Пусть векторы 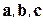заданы своими декартовыми координатами

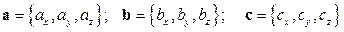
Смешанное произведение этих векторов определяется формулой:

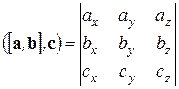(1.24)

Докажите эту формулу, опираясь на определение смешанного произведения, формулы (1.16), (1.23) и материал раздела (1.6).

Число 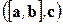по абсолютной величине равно объему параллелепипеда, построенного на векторах 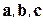. Знак числа 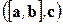– "плюс" или "минус" в зависимости от того, правую или левую тройку образуют векторы .

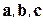Действительно, пусть 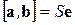. Здесь 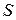– площадь параллелограмма, построенного на векторах 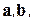вектор 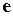- орт векторного произведения 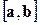. Тогда

,

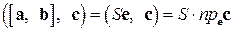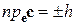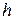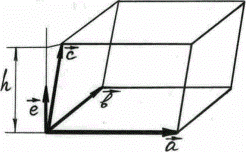
но , где - высота параллелепипеда. Значит, 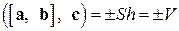. Рис.14

На рис. 14 изображен случай, когда тройка 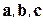– правая, то есть .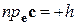

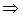
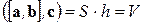Необходимое и достаточное условие компланарности векторов 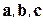– равенство нулю их смешанного произведения. В декартовой системе координат условие компланарности трех векторов принимает вид:

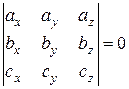(1.25)

Задача 1. Доказать, что .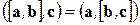

Указание. Показать, что эти числа равны по модулю и имеют одинаковые знаки. ¨

Заметим, что теперь имеем право смешанное произведение обозначать 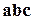, не указывая, какая пара векторов множится векторно.

Задача 2. Чему равно смешанное произведение векторов

?

Решение. По определению имеем 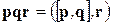. Вычислим сначала векторное произведение

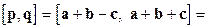
С учетом алгебраических свойств векторного произведения получаем 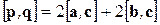. Осталось вычислить скалярное произведение

.

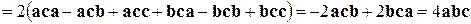Напоминаем, что тройк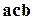и и 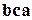имеют разную ориентацию, а тройки и 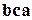ориентированы одинаково. Поэтому .

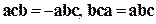Ответ. ¨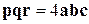

Задача 3. Определить, правой или левой является тройка 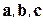, если

1) 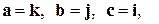2) .

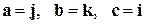Решение. Вычислим смешанное произведение 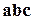по формуле (1.24).

В случае 1) 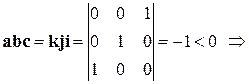тройка левая.

В случае 2) 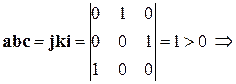тройка правая. ¨

Задача 4. Вектор 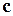ортогонален к векторам 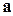и 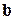, угол 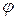между векторами 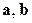равен 30^о, 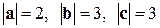. Вычислить смешанное произведение .

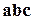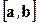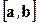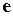Решение. Найдем сначала вектор . Если обозначим орт вектора через , то 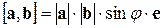. Следовательно,

.

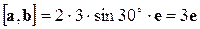Теперь найдем , тут 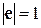, 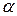– угол между векторам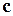и и .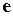

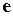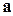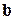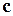Вектор по определению векторного произведения ортогонален каждому из векторов и и направлен так, что тройка правая. Вектор также ортогонален векторам 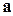и 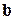(по условию), следовательно, он коллинеарен вектору 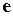, поэтому 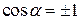. Знак "плюс" относится к случаю, когда векторы 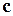и 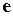одинаково направлены, то есть тройка 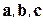правая. Знак "минус" - когда векторы 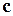и 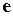направлены противоположно, то есть тройка 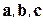левая. Значит,

. ¨

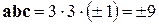Задача 5. Вычислить объем 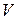параллелепипеда, построенного на векторах .

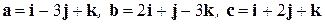Решение. Найдем смешанное произведение векторов 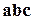по формуле (1.24):

.¨

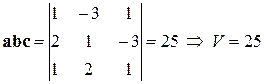Задача 6. Вычислить объем параллелепипеда, построенного на векторах .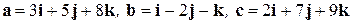

Ответ. 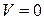, то есть данные векторы компланарны ¨

Задача 7. Вычислить объем тетраэдра с вершинами в точках

.

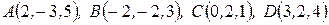Решение. Сначала найдем координаты векторов :

.

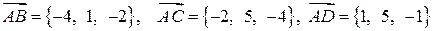Теперь вычислим смешанное произведение этих векторов, а затем и объем 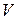параллелепипеда:

.

Объем 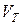тетраэдра в шесть раз меньше (почему?): . ¨

Задача 8. Проверить, являются ли заданные векторы линейно зависимыми

.

Решение. Найдем по формуле (1.24) смешанное произведение данных векторов:

.

Следовательно, векторы компланарны, поэтому линейно зависимы.¨

Задача 9. Проверить, лежат ли в одной плоскости точки

.

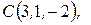
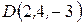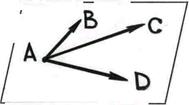
Решение. Точки 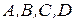лежат в одной плоскости тогда и только тогда, когда векторы 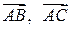и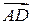

компланарны (рис. 15). Рис.15

Запишем координаты векторов: .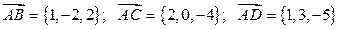

Вычислим смешанное произведение по формуле (1.24):

Видим, что условие компланарности не выполняется, значит, точки 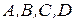не лежат в одной плоскости ¨

Задача 10. Доказать, что векторы 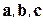компланарны, если

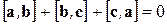. (1.26)

Решение. Умножим обе части равенства (1.26) скалярно, например, на вектор 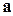: 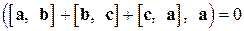. По свойствам скалярного произведения последнее равенство приобретает вид:

.

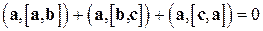По определению смешанного произведения получили 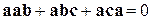. Но тройка 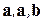содержит два одинаковых вектора, поэтому , также 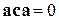. Остается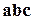 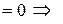векторы 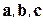компланарны. ¨

Двойным векторным произведением трех векторов 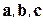называем произведение 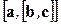, где сначала векторы 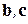перемножаются векторно, а вектор 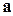множится на результат снова векторно. Следовательно, двойное векторное произведение - это вектор.

Двойное векторное произведение можно вычислить по формуле

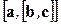
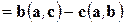(1. 27)

Задача 11. Проверить справедливость равенства

.

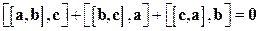Решение. Каждое из слагаемых вычислим по формуле (1.27) (по формуле "бац минус цаб"):

,

,

.

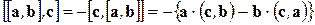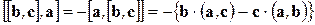Учитывая коммутативность скалярного произведения, получаем:

. ¨

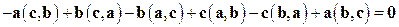1. Вычислить объем параллелепипеда, построенного на векторах: ; ; .
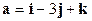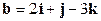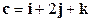2. Проверить, компланарны ли данные векторы:

1) ; ;

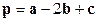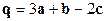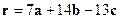
2) ; ; .

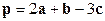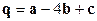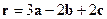Здесь 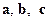– взаимно перпендикулярные единичные векторы.

1. Проверить, компланарны ли данные три вектора:

1) , , ,

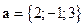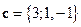2) , , .

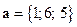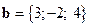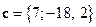1. Убедиться, что четыре точк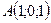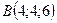и , , и 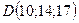лежат в одной плоскости.
2. Правую или левую тройку образуют векторы , , ?
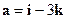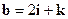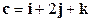3. Вершины треугольной пирамиды находятся в точках: 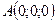, , 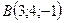, 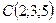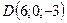. Вычислить ее объем.
4. Заданы векторы 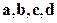. Доказать, что векторы 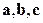образуют базис в 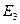и найти координаты вектора 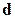в этом базисе.

1) , , , ;

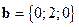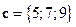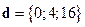2) , , , .

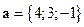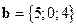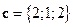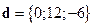1. Даны координаты вершин пирамиды 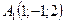, , 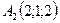, 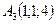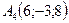. Найти:

1) длину ребер ; ; ;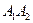

2) угол между ребрам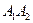и и ;

3) площадь грани ;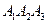

4) объем пирамиды;

5) длину высоты, опущенной из вершины 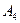на грань .

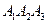9. При каких значениях параметра 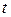векторы 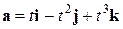, , 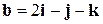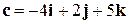компланарны?

Дата добавления: 2014-11-06