Ol — V2X 2 страница

Выведенные нами неравенства являются условиями равнове­сия. Их выполнение, однако, еще недостаточно для того, чтобы равновесие было полностью устойчивым.

Именно, могут существовать такие состояния, при бесконечно малом отклонении от которых энтропия уменьшается, так что тело вслед за этим возвращается в исходное состояние, в то время как при некотором конечном отклонении энтропия может ока­заться большей, чем в исходном состоянии. При таком конечном отклонении тело не вернется в исходное состояние, а наоборот, будет стремиться перейти в некоторое другое состояние равновесия, соответствующее максимуму энтропии, большему, чем максимум энтропии в первоначальном состоянии. Соответственно этой воз­можности среди состояний равновесия надо различать так назы­ваемые метастабильные и стабильные состояния. Если тело находится в метастабильном состоянии, то при достаточном откло­нении от него тело может не вернуться в исходное состояние. Хотя метастабильное состояние в известных пределах устойчиво, но рано или поздно тело все равно перейдет из него в другое, стабильное состояние. Последнее соответствует наибольшему из всех возможных максимумов энтропии; выведенное из такого состояния тело рано или поздно вернется в него обратно.

§ 22. Принцип Ле-Шателье

Рассмотрим замкнутую систему, состоящую из среды и погру­женного в нее тела. Пусть S есть полная энтропия системы, а у — некоторая величина, относящаяся к телу, причем такая, что условие максимума S по отношению к ней, т. е. dS/dy = 0, означает, что.тело само по себе находится в равновесии, не находясь при этом обязательно в равновесии со средой. Пусть, далее, х есть другая термодинамическая величина, относящаяся к тому же телу, причем такая, что если, наряду с dS/dy = 0, имеет место также и dS/dx = 0, то это означает, что тело находится не только в своем внутреннем равновесии, но также и в равно­весии со средой.

Введем обозначения

* = -§-. ^=-f- (22,1)

При полном термодинамическом равновесии энтропия 5 должна быть максимальна. Для этого, кроме условий

Х=0, Г = 0, (22,2)

должны выполняться также неравенства

£)„^>0' (fi^>0' ⁽²²'³⁾

причем

(£).(£).-(£):>»■

Предположим теперь, что путем какого-либо незначительного внешнего воздействия нарушается равновесие тела со средой, причем несколько изменяется величина х и нарушается условие Х = 0; о величине же у предполагаем, что она данным воздейст­вием непосредственно не затрагивается. Пусть Доесть изменение величины х; тогда изменение величины X в момент воздействия будет

Изменение х при постоянном у приводит, конечно, к нару­шению также и условия У = 0, т. е. внутреннего равновесия тела. После того как это равновесие снова восстановится, вели­чина X == ДХ будет иметь значение

где производная берется при постоянном, равном нулю, значе­нии Y.

Сравним оба значения ДХ. Пользуясь свойствами якобианов, имеем

d(X,Y) fdX

(дХ \ __ д (X, Y) д (х, у) __(дХ\ \ ду

V дх)у^о~ д{х,У) ~~ д (х, Y) ~ { дх)_у f dY

д (х, у) \ ду

Знаменатель второго члена в этом выражении положителен со­гласно условию (22,3); учитывая также неравенство (22,4), нахо­дим, что

'^дХ\>(⁹£\ „>0, (22,5)

дх /у \ дх /у = о' ИЛИ

|(ДХХ,|>|(ДХ)у₌„|. (22,6)

Неравенства (22,5) или (22,6), составляют содержание так называемого принципа Ле-Шателье.

Будем рассматривать изменение Дх величины х как меру внеш­него воздействия на тело, а ДХ—как меру изменения свойств тела под влиянием этого воздействия. Неравенство (22,6) пока­зывает, что при восстановлении внутреннего равновесия тела после внешнего воздействия, выводящего его из этого равнове­сия, значение ДХ уменьшается. Поэтому принцип Ле-Шателье можно сформулировать так:

Внешнее воздействие, выводящее тело из равновесия, стиму­лирует в нем процессы, стремящиеся ослабить результаты этого воздействия.

Поясним сказанное примерами.

Прежде всего удобно несколько видоизменить определение величин X и Y, воспользовавшись формулой (20,8), согласно которой изменение энтропии системы среда + тело равно —R_mijT₀, где Т₀—температура среды, a R_mit]—минимальная работа, необ­ходимая для приведения тела из состояния равновесия со средой в данное. Поэтому можно написать:

Для бесконечно малого изменения состояния тела имеем (см. (20,4))

dR_min = (T-T₀)dS-(P~ P₀)dV;

все величины без индекса здесь и ниже относятся к телу, а с ин­дексом 0—к среде.

Пусть х есть энтропия тела S. Тогда X = (Т—Т^л/Т₀. Условие равновесия Х = 0 дает Т = Г„, т. е. равенство температур тела и среды. Неравенства (22,5) и (22,6) принимают вид

(£).>(£),..>". <²²'⁸>

|(ДГ)„|>|(ДГ)_У,.|. (22,9)

Смысл этих неравенств заключается в следующем. Изменение величины х—энтропии тела—означает, что телу сообщается (или от тела отнимается) некоторое количество тепла. В результате нарушается равновесие самого тела и, в частности, изменяется его температура (на величину (АТ)_у). Восстановление равновесия в теле приводит к тому, что изменение его температуры по аб­солютной величине уменьшится (станет равным (AT)_Y= ₀), т. е. как бы ослабляется результат воздействия, выводящего тело из равновесия. Можно сказать, что нагревание (охлаждение) тела стимулирует в нем процессы, стремящиеся понизить (повысить) его температуру.

Пусть теперь х есть объем тела V. Тогда Х = — (Р—Р₀)/Т₀. В равновесии Х = 0, т.е. Р = Р„. Неравенства (22,5) и (22,6)дают

(£).<(£),..«>. <²².'°>

|(ДР),|>|(4Я)у..|. (22,11)

Если тело выводится из равновесия путем изменения его объема (при неизменной температуре), то меняется, в частности, его давление; восстановление равновесия в теле приводит к умень­шению абсолютной величины изменения давления. Имея в виду,

§ 23]

ТЕОРЕМА HEPHCTA

что уменьшение объема тела увеличивает его давление (и наобо­рот), можно сказать, что уменьшение (увеличение) объема тела стимулирует в нем процессы, стремящиеся уменьшить (увеличить) его давление.

В дальнейшем мы встретимся с целым рядом различных при­менений этих результатов (к растворам, химическим реакциям и т. п.).

Отметим еще, что если в неравенствах (22,8) в качестве вели­чины у взять объем тела, то будем иметь

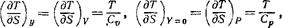
поскольку условие Y = 0 означает в этом случае Р = Р₀, т. е. постоянство давления. Таким образом, мы снова получаем из­вестные уже нам неравенства С_р > C_v > 0.

Аналогично, если в (22,10) в качестве у взять энтропию тела, то условие Y = 0 будет означать постоянство температуры Т — Т₀, и мы найдем

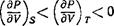
— тоже известный уже нам результат.

§ 23. Теорема Нернста

Тот факт, что теплоемкость C_v положительна, означает, что энергия есть монотонно возрастающая функция температуры. Напротив, при падении температуры энергия монотонно умень­шается, и, следовательно, при наименьшей возможной темпера­туре, т. е. при абсолютном нуле, тело должно находиться в со­стоянии с наименьшей возможной энергией. Если рассматривать энергию тела как сумму энергий частей, на которые можно мыс­ленно его разделить, то можно утверждать, что и каждая из этих частей будет находиться в состоянии с наименьшей энер­гией; ясно, что минимальному значению суммы должны соответ­ствовать и минимальные значения всех ее слагаемых.

Таким образом, при абсолютном нуле любая часть тела должна находиться в одном определенном—основном — квантовом состоя­нии. Другими словами, статистические веса этих частей равны единице, а потому равно единице и их произведение, т. е. ста­тистический вес макроскопического состояния тела в целом. Энт­ропия же тела—логарифм его статистического веса — равна, сле­довательно, нулю.

Поэтому мы приходим к следующему важному заключению: энтропия всякого тела обращается в нуль при абсолютном нуле

температуры (так называемая теорема Нернста (W. Nernst, 1906)^г).

Подчеркнем, что эта теорема является следствием квантовой статистики, в которой существенную роль играет понятие о ди­скретных квантовых состояниях. Она не может быть доказана в чисто классической статистике, в которой энтропия вообще определяется лишь с точностью до произвольной аддитивной постоянной (см. § 7).

Теорема Нернста позволяет сделать заключения и о поведении некоторых других термодинамических величин при 7-»-0. Так, легко видеть, что при 7 = 0 обращаются в нуль теплоемкости — как С_р, так и C_v:

C_p = C_v = 0 при 7 = 0. (23,1)

Это следует непосредственно из определения теплоемкости, напи­санного в виде

Р_ rpdS___ dS

^Ь~ df~dhTf-

При Т->0 имеем: lnT-s—оо, а поскольку S стремится к по­стоянному пределу (к нулю), ясно, что написанная производная стремится к нулю.

Далее, обращается в нуль коэффициент теплового расширения

{w)p ^{= 0 П}Р^{И г=0}- <²³'²)

Действительно, эта производная равна производной — (dS/dP)_T

(см. (16,4)), обращающейся при 7 = 0 в нуль, поскольку S = 0
при 7 = 0 и произвольном давлении.
Аналогично убеждаемся в том, что и

(§)_v = 0 при 7 = 0. (23,3)

Обычно энтропия обращается при 7->0 в нуль по степенному закону, т. е. как S = aTⁿ, где а—функция давления или объема. Очевидно, что в этом случае теплоемкости и величины (dV/dT)_P, (dP/dT)v обращаются в нуль по тому же закону (с тем же п).

Наконец, можно видеть, что разность С_р—С„ обращается в нуль быстрее, чем самые теплоемкости, т. е.

*) Во избежании недоразумений подчеркнем, что речь идет о стремлении температуры к нулю при каких-либо в остальном неизменных условиях—ска­жем, при постоянном объеме или постоянном давлении. Если же, например, стремить к нулю температуру газа одновременно с неорганиченным уменьше­нием его плотности, то энтропия может и не обратиться в нуль.

^^ = 0 при 7 = 0. (23,4)

Действительно, пусть при Т-+0 энтропия стремится к нулю по законуS ~ Т". Из формулы (16,9) видно, чтотогда C_p—C_v ~ Т^2п+1, так что (C„—C_l)/C_p^Tⁿ⁺¹ (следует иметь в виду, что сжимае­мость (дУ/дР)т остается при Т = 0, вообще говоря, отличной от нуля конечной величиной).

Если известна теплоемкость тела во всем диапазоне изменения температуры, то энтропия может быть вычислена путем интегри­рования, причем теорема Нернста позволяет установить значение постоянной интегрирования. Так, зависимость энтропии от тем­пературы при заданном значении давления определится по фор­муле

⁷С

S = §-f-dT. (23,5)

о

Для тепловой функции аналогичная формула гласит:

т

W = W.+ \c_pdT, (23,6)

о

где W₀—значение тепловой функции при Г —0. Для термоди­намического потенциала Ф = № — TS соответственно имеем

т т _с

Q> = W₀ + §C_pdT—T§-fidT. (23,7)

о о

§ 24. Зависимость термодинамических величин от числа частиц

Наряду с энергией и энтропией свойством аддитивности обла­дают также и такие термодинамические величины, как р, Ф, W (как это следует непосредственно из их определения, если учесть, что давление и температура постоянны вдоль находящегося в равновесии тела). Это свойство позволяет сделать определенные заключения о характере зависимости всех этих величин от числа частиц в теле. Мы будем рассматривать здесь тела, состоящие из одинаковых частиц (молекул); все результаты могут быть непо­средственно обобщены на тела, состоящие из различных частиц— смеси (см. § 85).

Аддитивность величины означает, что при изменении количе­ства вещества (а с ним и числа частиц N) в некоторое число раз эта величина меняется во столько же раз. Другими словами, можно сказать, что аддитивная термодинамическая величина должна быть однородной функцией первого порядка относительно адди­тивных переменных.

Выразим энергию тела в виде функции энтропии и объема, а также числа частиц. Поскольку 5 и V сами по себе тоже аддитивны, эта функция должна иметь вид

^E = ^Nf{lT>ir)' (24,1)

что является наиболее общим видом однородной функции первого порядка en N, S и V. Свободная энергия F есть функция от N, Т и V. Поскольку температура постоянна вдоль тела, а объем аддитивен, то из тех же соображений можно написать

(24,2)

Совершенно аналогично для тепловой функции W, выражен­ной в виде функции от N, S и давления Р, получим

W = Nf(±,p). (24,3)

Наконец, для термодинамического потенциала как функции от N, Р, Т имеем

Ф — Nf(P, Т). (24,4)

В предыдущем изложении мы по существу рассматривали число частиц как параметр, имеющий для каждого тела задан­ное постоянное значение. Будем теперь формально рассматривать N как еще одну независимую переменную. Тогда в выражения дифференциалов термодинамических потенциалов должны быть добавлены члены, пропорциональные dN. Например, для полного дифференциала энергии будем писать:

dE=*TdS- PdV+^dN, (24,5)

где посредством ц мы обозначили частную производную

Величина ц называется химическим потенциалом тела. Анало-
гично имеем теперь

dW = TdS + VdP + iLdN, (24,7)

dF = — SdT—PdV + pdN, (24,8)

d<b = — SdT-\-VdP+[idN (24,9)

с тем же \i. Из этих формул следует, что

-(»),.,-(£),.,-(»),.,• <²^>

т. е. химический потенциал можно получить дифференцированием любой из величин Е, W, F, Ф по числу частиц, однако при этом он окажется выраженным через различные переменные.

Дифференцируя Ф, написанное в виде (24,4), найдем, что и^дФ/dN = f(P, Т), т. е.

Ф = ЛГц. (24,11)

Таким образом, химический потенциал тела (состоящего из оди­наковых частиц) есть не что иное, как его термодинамический потенциал, отнесенный к одной молекуле. Будучи выражен в функ­ции от Р и Г, химический потенциал не зависит от N. Для диф­ференциала химического потенциала можно, следовательно, сразу написать следующее выражение:

dp = — sdT + vdP, (24,12)

где s и v—энтропия и объем, отнесенные к одной молекуле.

Если рассматривать (как мы до сих пор обычно делали) опре­деленное количество вещества, то число частиц в нем есть задан­ная постоянная величина, а его объем—величина переменная. Выделим теперь внутри тела некоторый определенный объем и будем рассматривать то вещество, которое заключено в этом объеме; при этом переменной величиной будет число частиц N, а объем V будет постоянным. Тогда, например, равенство (24,8) сведется к

dF = — SdT + iidN. Здесь независимыми переменными являются Т и N; введем такой термодинамический потенциал, для которого второй независимой переменной было бы не N, а ц. Для этого подставляем yidN^ = d(pJV)—JVdp, и получаем

d (F—tiN) = — SdT—N dp.

Ho [iN = Ф, a F—Ф = — PV. Таким образом, новый термодина­мический потенциал (который мы обозначим буквой fl) равен просто

Q = — PV, (24,13)

причем

dQ = — SdT — NdyL. (24,14)

Число частиц получается дифференцированием Q по химическому потенциалу при постоянных температуре и объеме:

"--[*)т.,-^У{*)т.Г <²⁴'¹⁵>

Подобно тому, как было доказано равенство между собой небольших изменений Е, W, F и Ф (при постоянных соответст­вующих парах величин) легко показать, что изменение (6Q)r, д, v при постоянных Т, p., V обладает тем же свойством. Иными словами,

фЕ)з, v,n = (Щт, v,n = (6Ф)г, р, n = (6W)_S, p,n = (Щт, v, ц. (24,16)

Эти равенства уточняют и расширяют теорему о малых добавках (15,12).

Наконец, аналогично тому, как это было сделано в §§ 15 и 20 для свободной энергии и термодинамического потенциала, можно показать, что работа при обратимом процессе, происходящем при постоянных Т, V и р, равна изменению потенциала Q. В состоя­нии же теплового равновесия потенциал Q имеет минимальное значение по отношению ко всякому изменению состояния при постоянных Т, V, \1.

Задач а

Получить выражение для теплоемкости C_v в переменных Т, ц., V. Ре шеи и е. Преобразуем производную C_V=T 0S/dT)v, n к переменным Т, V, fi, для чего пишем (рассматривая V все время как постоянную):

д (S, N) /dS\ fdN\

'^д1Л ₌d(s,N)_ d(T,_li) fds\ узц МагЛ*

_кдТ]\ д (Т, N) д (Т, N) -\дТ]ц fdN_\
д(Т,р) [дц)т

„ fdS \ d²Q (dN \

^Но Wh^-Wdrv&rti ^{поэтому}

{дт)„ (dN_\

\дц Jt)

§ 25. Равновесие тела во внешнем поле

Рассмотрим тело, находящееся в постоянном (во времени) внешнем поле. Различные части тела находятся при этом в раз­личных условиях, поэтому тело будет неоднородным. Одним из условий равновесия такого тела является по-прежнему постоян­ство температуры вдоль тела; давление же будет теперь различно в различных его точках.

Для вывода второго условия равновесия выделим из тела два определенных соприкасающихся объема и потребуем максималь­ности их энтропии S = S₁ + S_g при неизменном состоянии осталь­ных частей тела. Одно из необходимых условий максимума за­ключается в равенстве нулю производной dS/dN^ Поскольку общее число частиц Л^ + #₂ в двух данных частях тела рас­сматривается как постоянное, имеем

dS _ dS_t dS₂ dN₂ _ dS_t _ dS₂ _ _fl

Но из равенства dE==TdS-\~ndN, написанного в виде

dS = ~—^dN,

мы видим, что производная -Ц, (при постоянных ЕиТ) равна — и./7\

Таким образом, имеем: ii₁/T₁ = n_!s/T_a. Но при равновесии T_t — T_tt так что и р,₁ = (А₂. Мы приходим, следовательно, к результату, что при равновесии во внешнем поле, кроме постоянства темпе­ратуры должно соблюдаться условие

ц = const, (25,1)

т. е. химические потенциалы всех частей тела должны быть равны друг другу. При этом химический потенциал каждой части есть функция ее температуры и давления, а также параметров, опре­деляющих внешнее поле. Если поле отсутствует, то из посто­янства (I и Г автоматически следует и постоянство давления.

В поле тяготения потенциальная энергия молекулы и есть функция только координат х, у, z ее центра тяжести (и не за­висит от расположения атомов внутри молекулы). В этом случае изменение термодинамических величин тела сводится к добавле­нию к его энергии потенциальной энергии молекул в поле. В частности, химический потенциал (термодинамический потенциал, отнесенный к одной молекуле) примет вид р. = (А₀ -\-и(х, у, z), где fi₀ (Р, Т) есть химический потенциал в отсутствие поля. Таким образом, условие равновесия в поле тяготения можно написать в виде

ц₀ (Р, Т) + и (х, у, z) = const. (25,2)

В частности, в однородном поле тяжести u — tngz (m — масса молекулы, g— ускорение силы тяжести, z — вертикальная коор­дината). Дифференцируя равенство (25,2) по координате z при постоянной температуре, получим

vdP = —mgdz,

где v = (dnJdP)_T — удельный объем. При небольших изменениях давления v можно считать постоянным. Вводя плотность p = m/v и интегрируя, получим

Р — const—pgz,

т. е. обычную формулу для гидростатического давления в несжи­маемой жидкости.

§ 26. Вращающиеся тела

В состоянии теплового равновесия возможно, как мы видели в § 10, лишь равномерное поступательное движение и равномер­ное вращение тела как целого. Равномерное поступательное дви­жение никакого особого рассмотрения не требует, так как согласно принципу относительности Галилея оно никак не сказывается на механических, а потому и термодинамических свойствах тела, и его термодинамические величины меняются лишь в том смысле, что к энергии добавляется кинетическая энергия тела.

Рассмотрим тело, равномерно вращающееся вокруг неподвиж­ной оси с угловой скоростью Q. Пусть Е(р, q) есть энергия тела в неподвижной системе координат, a E'(p,q)—энергия в системе координат, вращающейся вместе с телом. Как известно из меха­ники, эти величины связаны друг с другом соотношением

E'{p,q) = E(p,q)-im.(p,q), (26,1)

где М(р, q)—момент импульса тела¹).

Таким образом, энергия Е' (р, q) зависит, как от параметра, от угловой скорости Q, причем

Усредняя это равенство по статистическому распределению и воспользовавшись формулой (11,3), получим

^дЕ' ^Л =—М, (26,2)

да s

где Е' — Е'(р, q), М = М(р, q)—средние (термодинамические) энер­гия и момент импульса тела.

На основании этого соотношения мы можем написать диффе­ренциал энергии вращающегося тела при заданном объеме в виде

dE'= Т dS — f\du. (26,3)

Для свободной энергии F' = E'—TS (во вращающейся системе координат) соответственно имеем

dF' = —5 dT — mdQ. (26,4)

Усредняя равенство (26,1), получим

£' = £—МЙ. (26,5)

Дифференцируя это равенство и подставляя (26,3), получим диф­ференциал энергии в неподвижной системе координат

dE = TdS + Qdtl. (26,6)

Для свободной энергии F = E—TS соответственно имеем

dF=—SdT+Qdm. (26,7)

Таким образом, в этих соотношениях независимой переменной

^х) См. I, § 39. Хотя произведенный там вывод формулы (39,13) основан на классической механике, но в квантовой теории в точности те же соотно­шения справедливы для операторов соответствующих величин. Поэтому все выводимые ниже термодинамические соотношения не зависят от того, какой механикой описывается движение частиц тела.

(26,8)

Как известно из механики, равномерное вращение в известном смысле эквивалентно появлению двух силовых полей: поля центро­бежных сил и поля кориолисовых сил. Центробежные силы про­порциональны размерам тела (они содержат расстояние до оси вращения); силы же Кориолиса от размеров тела не зависят вовсе. Благодаря этому обстоятельству влияние последних на термодинамические свойства вращающегося макроскопического тела совершенно ничтожно по сравнению с влиянием первых, и ими обычно можно полностью пренебречь¹). Поэтому условие теплового равновесия вращающегося тела получится просто подстановкой в (25,2) в качестве и (х, у, г) центробежной энергии частиц:

MP, T)-^^ = const, (26,9)

где Ро—химический потенциал покоящегося тела, т—масса моле­кулы, г — расстояние до оси вращения. По той же причине пол­ную энергию вращающегося тела Е можно написать в виде сум­мы его внутренней энергии (которую мы обозначим здесь пос­редством Е_т) и кинетической энергии вращения:

Е = Е_ВК + ^, (26,10)

где /—момент инерции тела относительно оси вращения. Надо иметь в виду, что вращение, вообще говоря, меняет распределе­ние масс в теле, поэтому момент инерции и внутренняя энергия тела сами, вообще говоря, зависят от Q (или от М). Лишь при достаточно медленном вращении эти величины можно считать постоянными, не зависящими от Q.

Рассмотрим изолированное равномерно вращающееся твердое тело с заданным распределением масс в нем. Поскольку энтропия тела есть функция его внутренней энергии, то в данном случае

s-s[b-$).

*) Можно показать, что в классической статистике кориолисовы силы вообще не влияют на статистические свойства тела—см. § 34.

Вследствие замкнутости тела его полная энергия и момент вра­щения сохраняются, а энтропия должна иметь максимальное зна­чение, возможное при данных М и Е. Поэтому мы приходим к выводу, что равновесное вращение тела происходит вокруг оси, относительно которой момент инерции имеет наибольшее возмож­ное значение. Тем самым автоматически подразумевается, что ось вращения во всяком случае является осью инерции тела. Послед­нее обстоятельство, впрочем, заранее очевидно: если тело вра­щается вокруг оси, не являющейся осью инерции, то, как известно из механики, ось вращения сама будет смещаться (прецессиро-вать) в пространстве, т. е. вращение будет неравномерным, а потому и неравновесным.

§ 27. Термодинамические соотношения в релятивистской области

Релятивистская механика приводит к ряду изменений в обыч­ных термодинамических соотношениях. Мы рассмотрим здесь те из этих изменений, которые представляют наибольший интерес.

Если микроскопическое движение частиц, составляющих тело, становится релятивистским, то общие термодинамические соотно­шения не изменяются, но возникает важное неравенство между давлением и энергией тела

р<4г- (ад

где Е—энергия тела, включающая в себя энергию покоя вхо­дящих в его состав частиц¹).

Принципиальный интерес представляют изменения, вносимые общей теорией относительности в условиях теплового равновесия при учете создаваемого самим телом гравитационного поля. Рас­смотрим неподвижное макроскопическое тело; его гравитационное поле будет, разумеется, постоянным. В постоянном гравитацион­ном поле надо отличать сохраняющуюся энергию Е₀ какой-либо малой части тела от энергии Е, измеренной наблюдателем, нахо­дящимся в данном месте; эти две величины связаны друг с дру­гом соотношением

E_a = EVg^,

^х) См. II, § 35. Напомним, однако, что общего доказательства этого нера­венства, пригодного для всех существующих в природе (не только электро­магнитных) типов взаимодействия между частицами, в настоящее время не существует.

где g₀₀—временная компонента метрического тензора (см. II, §88; формула (88,9) с у = 0, тс² = Е). Но по самому смыслу приве­денного в § 9 доказательства постоянства температуры вдоль на­ходящегося в равновесии тела ясно, что должна быть постоянна величина, получающаяся дифференцированием энтропии по сох­раняющейся энергии Е₀. Температура же Т, измерепная наблю­дателем, находящимся в данной точке пространства, получается дифференцированием энтропии по энергии Е и, следовательно, будет различна в разных точках тела.

Для вывода количественного соотношения замечаем, что энтро­пия по существу своего определения зависит исключительно от внутреннего состояния тела и потому не изменяется при появле­нии гравитационного поля (в той мере, в которой это поле не влияет на внутренние свойства тела, —условие, которое факти­чески всегда выполнено). Поэтому производная по энтропии от сохраняющейся энергии Е„ будет равна T\f g_m и, таким образом, одно из условий теплового равновесия требует постоянства вдоль тела величины

TVlfa = const. (27,2)

Аналогичным образом видоизменяется второе условие равно­весия— постоянство химического потенциала. Химический потен­циал определяется как производная от энергии по числу частиц. Поскольку число частиц, разумеется, гравитационным полем не меняется, то для химического потенциала, измеренного в каждой данной точке, получаем такое же соотношение, как и для тем­пературы:

pKi^ = const. (27,3)

Заметим, что соотношения (27,2—3) можно написать в виде

T = const~, ii = consb-^, (27,4)

позволяющем рассматривать тело не только в той системе отсчета, в которой оно неподвижно, но и в таких, в которых оно дви­жется (вращается как целое). При этом производная dx°/ds должна браться по мировой линии, описываемой данной точкой тела.

В слабом (ньютоновском) гравитационном поле g₀₀ = 1 -f-2cp/c², где ср — гравитационный потенциал (см. II, § 87). Подставляя это выражение в (27,2) и извлекая корень, найдем в том же приближении

Г = const- (l—J). (27,5)

Имея в виду, что ср < 0, находим, что при равновесии темпера­тура выше в тех местах тела, в которых | ср | больше, т. е. в глубине тела. При предельном переходе к нерелятивистской механике (с—► оо) (27,5) переходит, как и следовало, в Т = const.

Аналогичным образом можно преобразовать условие (27,3), причем надо иметь в виду, что релятивистский химический потен­циал при предельном переходе к классической механике переходит не непосредственно в обычное (нерелятивистское) выражение для химического потенциала в отсутствие поля, которое мы обозна­чим здесь посредством р,₀, а в p₀-f-mc², где ж²—энергия покоя

отдельной частицы тела. Поэтому имеем

И Vffa ~ О*, +mc²) (l wц, + mc^% + m<p,

Дата добавления: 2014-11-07