Ol — V2X 9 страница

где g=2s-\-\, s—спин частицы, т.е. равно

Интегрируя по dV (что сводится к замене dV на полный объм V газа), получим распределение по компонентам импульса частиц, а переходя к сферическим координатам в пространстве импульсов и интегрируя по углам, найдем распределение по абсолютной величине импульса

dN_p= . ff*?,_T г, (56,3)

(где £ = p²/2m), или распределение по энергии

,,, gVm^3/2 Vide _/сс

Эти формулы заменяют классическое распределение Максвелла. Интегрируя (56,4) по de, получим полное число частиц в газе

_{= g}Vm^3li Г У в de

2^1/алФ J **-М^т± 1 '

Вводя новую переменную интегрирования г/Т = г, перепишем это равенство в виде

N g(mT)*<'* р VTdz о

Эта формула определяет в неявном виде химический потенциал газа р- как функцию от температуры Т и плотности N/V..

§ 56] ферми- и бозе-газы элементарных частиц 185

Совершая такой же переход от суммирования к интегрирова­нию в формулах (53,4), (54,4), получим следующее выражение для потенциала й:

3/2 °°

Q = op ^Vf.f! [У~г In (1 ± e^-^^T)de. о

Интегрируя по частям, находим

_п 2 gVm^s/i } е^3/а йъ _{/KR R}.

^У=~Т ₂1/«яФ j ^-ц)/т_±1 • (^5ь-^ь)

Это выражение совпадает с точностью до множителя —2/3 с полной энергией газа, равной

с Г jh gFm^s/2 Г e^3/2de,-_с „

Имея также в виду, что Q = — PV, получаем, таким образом, следующее соотношение:

PV=jE. (56,8)

Будучи точным, это соотношение должно выполняться и в пре­дельном случае больцмановского газа; действительно, подстав­ляя больцмановское значение Е = 3NT/2, получим уравнение Клапейрона.

Из формулы (56,6), сделав подстановку 8/7' = г, найдем, что

Q = —PV = VT*'*f (f), (56,9)

где /—функция от одного аргумента, т. е. Q/V есть однородная функция (I и Г порядка 5/2¹). Поэтому

V * V\dT)v,» V ~~ 7 1.3(1 У г, v

— однородные функции ц и Т порядка 3/2, а их отношение S/Л⁷-— однородная функция нулевого порядка: S/N = ц> (ц/Т). Отсюда видно, что при адиабатическом процессе (S = const) остается

E = N^+TS-PV^-^-T^ + Q,

^А) Если по выражению (56,9) вычислить энергию как E = Nn+TS—i то мы снова получим соотношение (56,8)

постоянным отношение ii/T, а поскольку N/VT^3/t тоже есть функ-
ция только от р./7\ то и

= const. (56,10)

Тогда из (56,9) следует, что

рум = const, (56,11)

а также и T^s/2/P = const. Эти равенства совпадают с уравнением адиабаты Пуассона (43,9) для обычного одноатомного газа. Под­черкнем, однако, что показатели степени в формулах (56,10—11) не связаны теперь с отношением теплоемкостей (поскольку не­справедливы соотношения c_p/c_v = 5/3 и с_р—c_v= 1). Формула (56,6), переписанная в виде

^р- Ш^з \ ^(56,12)

вместе с формулой (56,5) определяют в параметрическом виде (параметром является р.) уравнение состояния газа, т. е. связь между Р, V и Т. В предельном случае больцмановского газа (чему соответствует е^'^Т<^.1) из этих формул получается, как и должно было быть, уравнение Клапейрона. Покажем это, вычи­слив одновременно также и первый поправочный член разложе­ния в уравнении состояния.

При е^^т<^. 1 разлагаем подынтегральное выражение в (56,12)
в ряд по степеням и получаем, сохраняя два первых

члена разложения,

Подставляя это в (56,12), имеем

"~ ^FV~ (2я)"**» ^В V⁺ 2»/» ⁶ J'

Если сохранить лишь первый член разложения, то получим в точности больцмановское значение химического потенциала одноатомного газа (формула (46,1а)). Следующий же член дает искомую поправку, так что можно написать:

Но малые добавки ко всем термодинамическим потенциалам (выраженные через соответствующие переменные, см. (24,16)),

одинаковы. Поэтому, выразив поправку в Q через Т и V (что можно сделать с той же точностью с помощью больцмановских выражений), мы получим поправку к свободной энергии:

дЗ/2 д^з

/⁷ = ^больц±-Т^-_]/г1/2тз_/2- (56.14)

1 + -

(56,15)

Наконец, дифференцируя по объему, получим искомое уравнение состояния

3/2

я³''² АФ 1

PV^NT

2g V(mT)

Условие малости поправочного члена в этой формуле совпадает, естественно, с условием (45,6) применимости статистики Больц­мана. Таким образом, отклонения свойств идеального газа от классических, возникающие при понижении температуры при заданной плотности (как говорят, при начинающемся его вырож­дении), ведут в статистике Ферми к увеличению давления по сравнению с его значением в обычном газе; можно сказать, что квантовомеханические обменные эффекты приводят в этом случае к появлению некоторого дополнительного эффективного отталки­вания между частицами.

В статистике же Бозе величина давления газа отклоняется в обратную сторону—в сторону уменьшения по сравнению с клас­сическим значением; можно сказать, что здесь появляется неко­торое эффективное притяжение между частицами.

§ 57. Вырожденный электронный газ

Важное принципиальное значение имеет изучение свойств ферми-газа при достаточно низких температурах. Как мы увидим ниже, температуры, о которых при этом идет речь, фактически могут еще быть, с других точек зрения, весьма высокими.

Имея в виду наиболее важные применения статистики Ферми, будем говорить ниже об электронном газе; соответственно этому полагаем g=2 (спин s= 1/2).

Начнем с рассмотрения электронного газа при абсолютном нуле температуры (полностью вырожденный ферми-газ). В таком газе электроны будут распределены по различным квантовым состояниям таким образом, чтобы полная энергия газа имела наименьшее возможное значение. Поскольку в каждом кванто­вом состоянии может находиться не более одного электрона, то электроны заполнят все состояния с энергиями от наименьшей (равной нулю) до некоторой наибольшей, величина которой опре­деляется числом электронов в газе.

С учетом двукратного (g=2) спинового вырождения уровней, число квантовых состояний электрона, движущегося в объеме V

распределения ферми и бозе

[гл. V

с абсолютной величиной импульса в интервале между р и p-\~dp, равно

(2я£)³ яФ ^v ' '

Электроны заполняют все состояния с импульсами от нуля до граничного значения р = р_р; об этом значении говорят как о ра­диусе ферми-сферы в импульсном пространстве. Полное число электронов в этих состояниях

# = -т- fP*dp

ЗлФ '

откуда для граничного импульса имеем

N \ 1/з

(57,2)

и для граничной энергии

Р (N\²'³

(57,3)

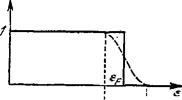
Эта энергия имеет простой термодинамический смысл. В со­гласии со сказанным выше функция распределения Ферми по

квантовым состояниям (с опреде­ленными значениями импульса р и проекции спина)

¹ (57,4)

+ 1

в пределе Т—► () обращается в
«ступенчатую» функцию: единица
р_ис е. при е < р. и нуль при е > ц (на

рис. 6 эта функция изображена сплошной линией). Отсюда видно, что химический потенциал газа при Г = 0 совпадает с граничной энергией электронов:

u. = e_f. (57,5)

Полная энергия газа получится умножением числа состояний (57,1) на р²/2ш и интегрированием по всем импульсам:

Рр

V f Voi.

2тяФ

ЮтпФ '

Е=;—^ГТ J рЧр=-

или, подставив (57,2):

Е =

3 (Зя²)^2/3 Р [ N \2^/3

N.

(57,6)

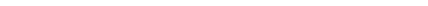Таким образом, давление ферми-газа при абсолютном нуле тем­пературы пропорционально его плотности в степени 5/3.

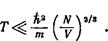
Полученные формулы (57,6—7) применимы приближенно так­же и при температурах, достаточно близких (при данной плот­ности газа) к абсолютному нулю. Условие их применимости (условие «сильного вырождения» газа) требует, очевидно, малости Т по сравнению с граничной энергией г_р:

(57,8)

Это условие, как и следовало ожидать, противоположно условию (45,6) применимости статистики Больцмана. Температуру Т_Рже_Р называют температурой вырождения.

Вырожденный электронный газ обладает своеобразной особен­ностью— он становится тем более идеальным, чем больше его плотность. В этом легко убедиться следующим образом.

Рассмотрим плазму—газ, состоящий из электронов и соответ­ствующего количества положительно заряженных ядер, компен­сирующих заряд электронов (газ из одних только электронов был бы, очевидно, вообще неустойчивым; выше мы не говорили о ядрах, поскольку вследствие предполагающейся идеальности наличие ядер не сказывается на термодинамических величинах электронного газа). Энергия кулонового взаимодействия электро­нов с ядрами (отнесенная к одному электрону) порядка величи­ны Ze²/a, где Ze—заряд ядра, a a~(ZV//V)^1/3 —среднее расстояние между электронами и ядрами. Условие идеальности газа заклю­чается в требовании малости этой энергии по сравнению со сред­ней кинетической энергией электронов, которая по порядку ве­личины совпадает с граничной энергией s_P. Неравенство

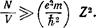
после подстановки а ~ (ZV/N)^1/3 и выражения (57,3) для e_F дает условие

(57,9)

*) Температура вырождения, соответствующая плотности электронного газа, равной (e²mi%²f Z², составляет40 Z^4/3sew0,5-10⁶Z^4/'³ градусов.

Мы видим, что это условие выполняется тем лучше, чем больше плотность газа N/V¹).

Задача

Определить число столкновений со стенкой в электронном газе при абсо­лютном нуле температуры.

Решение. Число электронов (в единице объема) с импульсами в интервале dp, направленными под углом к нормали к стенке в интервале dQ, есть

2-2я sin 0 <Юр²ф (2я&)³

Искомое число столкновений v (отнесенное к I см² стенки) получается умноже­нием на v cos 0 (v = р/т) и интегрированием по dQ в пределах от 0 до я/2 и по dp—от 0 до pp. В результате найдем

3(3я²)^1/3 % (N \^4/3

16 т \ V

§ 58. Теплоемкость вырожденного электронного газа

При температурах, низких по сравнению с температурой вы­рождения T_F, функция распределения (57,4) имеет вид, изобра­женный на рис. 6 пунктирной линией: она заметно отлична от единицы или нуля лишь в узком интервале значений энергии 8,близ­ких к граничной энергии г_Р. Ширина этой, как говорят, зоны размытости распределения Ферми—порядка величины Т.

Выражения (57,6—7) представляют собой первые члены раз­ложения соответствующих величин по степеням малого отношения Т/Т_Р. Определим следующие члены этого разложения.

В формулу (56,6) входит интеграл вида

/ (е) de.

+ 1

где [(г) — некоторая функция (такая, что интеграл сходится); в (56,6) f(e) = e^3/2. Преобразуем этот интеграл, сделав подста­новку е—ц = Тг:

и/т

/Qi + Гг) dz е^г+1

-ц/Г 0 0

В первом интеграле пишем

_L_ _{= 1} L_

е~^г+1 е^г+1

и находим

/ = |/(_e)de-rf^^ ₊ TJOi^₍

Во втором интеграле заменяем верхний предел бесконечностью, имея в виду, что ц/Т^>\, а интеграл быстро сходится¹). Таким образом, получим

i=lmdB+T]^+^T%-\^dz.

о о

Разлагаем теперь числитель подынтегрального выражения во втором интеграле в ряд Тэйлора по степеням г и интегрируем почленно:

pi со со

0 0 о

Подставляя значения интегралов²), имеем окончательно

/ = j f (8) ds + ^ T*f (р.) +|РГМ+... (58,1)

о

^J) Эта замена означает пренебрежение экспоненциально малыми ч пенами. Надо иметь в виду, что получающееся ниже разложение (58,1) представляет собой асимптотический (а не сходящийся) ряд.

²) Интегралы такого типа вычисляются следующим образом:

» со _м

J 9+х=1^гХ~^ч~^г Ё⁽~^)п

0 0 я=0

= Г (х) £ (-)» +»± = (1-21-*) Г (*) 2,

л=1 п=1

или

со

£^£5+х=<¹-²¹-*)^гмсм <*>°)-

о

где £(х)— £-функция Римана. При х—1 это выражение дает неопределенность; значение интеграла

о

При целом четном х(*=2п) ^-функция выражается через так называемые числа Бернулли В_п, и получается

со

о

Аналогичным образом вычисляются следующие интегралы:

Третий член разложения приведен для справок; здесь он нам не понадобится.

Полагая в формуле (58,1) / = е^3/2 и подставляя в (56,6), полу­чим искомый следующий член разложения потенциала Q при низких температурах:

Q = Q₀—VT'l^f- ■ (58,2)

Посредством Q₀ обозначена величина Q при абсолютном нуле температуры.

Рассматривая второй член как малую добавку к Q₀ и выра­жая в нем [I через Г и У с помощью «нулевого приближения» (57,5), мы можем непосредственно написать выражение для сво­бодной энергии (согласно теореме о малых добавках (24,16)):

_F==Fe-±_NT*(V_y\ ₍₅₈₍3)

где мы ввели для краткости обозначение

МтГг,- (58-4)

з; р-

Отсюда находим энтропию газа

s = w(jry. (58,5)

его теплоемкость^х)

C = pNT[U^t/\ (58,6)

о

При целом четном х=2п имеем

J e^z— 1 ~ 4я о

Приведем для справок несколько первых чисел Бернулли и несколько значений £-функций:

я ¹ и ¹ д - ¹ В -1-

С (3/2) = 2,612, С (5/2)= 1,341, 2(3) = 1,202, g <5) = 1,037;

Г (3/2) = Г (5/2) = 3 Уп /4.

^г) Мы не пишем индекса v или р у теплоемкости, так как в этом прибли­жении C_v и С_р совпадают. Действительно, мы видели в J 23, что если S стре­мится при Т—*0 к нулю, как Т", то разность C_p—C_v обращается в нуль, как Т^2и+1; в данном случае, следовательно,

C_p-C_vv>T*.

и энергию

= £, 1 + 0,18

(

(58,7)

Q (ц) = у О, (ц + ВЯ) + ~ Q₀ (р-ВЯ),

(59,2)

^J) В обратном случае высоких температур (Т ^> е_Р) электроны образуют больцмановский газ, и парамагнитная часть его восприимчивости, отнесенная к единице объема; Хпара ^{= лг}Р²/^ (формула (52,8) с g=2,

у = 1/2).

где Q₀(p)—потенциал в отсутствие поля (аргументы Т, V для

краткости не выписываем); два члена в этой сумме отвечают совокупностям электронов с различными проекциями спина, а множители 1/2 учитывают уменьшение вдвое числа квантовых состояний электрона при фиксировании значения проекции его спина.

Произведя в (59,2) разложение по степеням 6Я, получим

QM^QoM+yP²^-^, (59,3)

<3²р_

откуда магнитный момент Ш = —Щ²-~. Но производная

dQ₀/du. = — N, так что парамагнитная восприимчивость, которую в этом параграфе относим к единице объема газа:

у__________ E!^o ₌ P_²W (59 4)

Лпара— у ^2 у ^<J|1 / T,v' W.^-*/

Пренебрегая малым (при Т<^.\х) температурным эффектом, т. е. считая газ полностью вырожденным, имеем из (57,3)

Зл²П³ '

и дифференцирование дает

Хпара - ------ ТГ^Г*--------- ----------- ■ (^&У>^

Р² (2т)³/^а /р7 _ « 2яФ ~" яФ

Обратимся к вычислению диамагнитной восприимчивости. Уровни энергии орбитального движения электрона в магнитном поле даются выражением

е = 5| + (2л + 1)РЯ, (59,6)

где,г = 0, 1, 2, а р_г—импульс в направлении поля — про­бегает непрерывный ряд значений от —со до оо (см. III, § 112). При этом число состояний в интервале dp_z при каждом задан­ном значении п есть

где множитель 2 учитывает два направления спина. Выраже­ние (53,4) для потенциала Q принимает вид

0 = 2рЯ 2 Л> —(2л + 1)рЯ], (59,8)

Сумму (59,8) можно вычислить с требуемой точностью с по­мощью формулы¹)

fv(n+|)«]f (x)dx + ±f'(0). (59,10)

п=0

Условие применимости этой формулы состоит в малости относи­тельного изменения функции f на одном шаге (п-*-п + 1). В при­менении к функции (59,9) оно сводится к требованию 6Я<^Г²). Применив (59,10) к сумме (59,8), получим

— со

Первый член не содержит Я, т. е. представляет собой потен­циал Q₀ (и.) газа в отсутствие поля. Таким образом,

Q = Q₀(|i)—1в²Я²^|^, (59,11)

и отсюда восприимчивость³)

Хдиа ⁼ зу 3^2 ⁼ "з" Хпара-

(59,12)

В целом газ парамагнитен с восприимчивостью х = 2хпа_Ра/3-Мы произвели здесь вычисление обеих ее частей по отдельности с целью уяснения их происхождения. Разумеется, можно было бы вычислять также и сразу суммарную восприимчивость Для этого надо было бы писать уровни энергии электронов

^х) Согласно известной формуле суммирования Эйлера—Маклорена

1F (а) + 2 F (а + «) «J F (*) ^ ^f' <^а>- (⁵⁹-^10а)

л= 1 а

Формула (59,10) получится отсюда, если положить а=1/2 и представить функ­цию F (х) в интервале 0«5л:<1/2 в виде F (х) и F(0) + ^f'(0).

²) В противном случае условие нарушается в «опасной» области значе-
ний п, для которых разность р,—(2я-|-1)РЯ близка к нулю. Эта область
приводит (см. следующий параграф) к появлению в Q быстро осциллирующих
(как функция от Я) членов. Эти члены исчезнут, если произвести усреднение
ряда (59,8) по некоторому интервалу ДЯ такому, что изменение аргумента
р.—2р«Я (вблизи точки, где ц.—2|3л# я 0) будет существенно больше, чем
разность его двух соседних значений: ря <5с; л$ ДЯ ~ ц ЛЯ/Я или ДЯ/Я ^>
^рЯ/ц. После этого формула (59,10) станет вновь применима, и получаю-
щийся с ее помощью результат будет ограничен лишь условием рЯ <^ ц.

³) Отметим, что это соотношение справедливо при любой степени вырож-
дения газа.

в виде e = pf/2m + (2ra + l) рЯ± РЯ, получающемся прибавле­нием к (59,6) спиновой магнитной энергии ±РЯ. Эту совокуп­ность значений е можно представить и как

e=ij + 2np#, «= 0, 1, 2,... (59,13)

причем каждое значение с п^О встречается дважды, а с п = 0 один раз; другими словами, плотность числа состояний с пфО дается той же формулой (59,7), а для п = 0 она вдвое меньше. Потенциал Q определится тогда суммой

С ^

□ = 2ВЯ{1/(р.)+Х/ал-2ВЯя)}, (59,14)

а для ее вычисления надо воспользоваться формулой¹)
1 ⁰⁰ "г 1

£F (0)^f (") =.! F(x)dx-±F'(0). (59,15)

n=l 6

§ 60. Магнетизм электронного газа. Сильные поля

Рассмотрим теперь поля, для которых значение ВЯ, по-преж­нему малое по сравнению с р,, уже не должно быть малым по сравнению с Т:

Г^рЯ^р,. (60.1)

В этих условиях эффекты квантования орбитального движения и спиновые эффекты уже не могут быть отделены друг от друга и должны учитываться одновременно; другими словами, при вычислении Q надо исходить из выражения (59,14).

Мы увидим, что намагниченность электронного газа при РЯ^Т содержит часть, которая, как функция Я, осциллирует с большой амплитудой; именно эта осциллирующая часть намаг­ниченности и будет интересовать нас здесь.

Для выделения из термодинамических величин их осцилли­рующих частей целесообразно преобразовать сумму (59,14) с по­мощью формулы Пуассона ²):

со оо 00 оо

^x) Она получается из формулы Эйлера—Маклорена, если положить в ней а = 0. ²) Эта формула следует из равенства со со 2 6 (* — /») = 2 ^e2nlkXi сумма 6-функций в левой стороне этого равенства представляет собой периоди­ческую функцию переменной х с периодом 1, а сумма в правой стороне есть

Т F (0) +Е F («) = \ F (х) dx + 2 Re £ fF (x)e™^ik*dx, (60,2)

после чего она принимает вид

® = ^Qo(v)+^ReT*h, (60,3)

TmV

где

i„= -m jjln[l+exp(f~^-^)]e«-»*d«dA, (60,4)

-со 0

a Q„(fi)—термодинамический потенциал в отсутствие поля.

Произведем в интегралах 1_к замену переменной х на е = рЦ2т-\-+ 2х$Н. Для интересующей нас осциллирующей части интегра­лов (которую обозначим через f_k) получим

/, = - | ]ы[l +e*p(H=J)]вхр(^)ехр(--» о

В интеграле по /?_г существенны значения pf/2/n ~ В#. Осцилли­рующая же часть интеграла возникает от области значений е вблизи р, (см. ниже); поэтому нижний предел интегрирования по в заменен нулем (вместо р\\2т).

Интегрирование по р_г отделяется и осуществляется формулой^J)

to

после чего остается

_

7_А = __е-«я/4 т/ЩИ J in [1 +_е(д-в)/г]_еМЕ/зя^е.. о

разложение этой функции в ряд Фурье. Умножив равенство на произвольную функцию F (х) и проинтегрировав его затем по х от 0 до оо, получим (60,2) оо (при этом интеграл ^ F (х) б (х) dx—член суммы с я = 0, распространенный о лишь по области с одной из сторон от точки х = 0, дает F(0)/2). ^J) Она получается путем поворота пути интегрирования в плоскости ком­плексной переменной р: полагаем р=е~^1Л* и и интегрируем по вещественным значениям а от —оо до оо.

В этом интеграле производим дважды интегрирование по частям, а в остающемся интеграле производим замену переменной

(е—и.)/Г = |. Опустив неосциллирующую часть, получим

Нижний предел интеграла по |, равный —р/Т, в силу условия Р5>>Т заменен на —оо. При ВЯ^Г определяющую роль в ин­теграле играет область |~ 1, т. е. окрестность значений е во­круг р(е—u.~ Т). Интеграл вычисляется по формуле¹)

(*Ч1)^:

^: sh па•

Окончательно для осциллирующей части Q находим

_{й =} У2_(тт^ту^ ~(|£*-т). ₀₅₎

При вычислении магнитного момента как производной от вы­ражения (60,5), дифференцированию должны подвергаться лишь наиболее быстро меняющиеся множители—косинусы в числите­лях членов суммы. Это дает

m=-^f^fX^TVyL^sm_r-^^{H Tj} (60,6)

пр Vli f?_x Y k sh (я²/гГ/рЯ) ^{V 7}

(Л. Д. Ландау, 1939). Эта функция осциллирует с большой ча­стотой. Ее «период» по переменной 1/Я есть постоянная величина

A-i = f, (60,7)

не зависящая от температуры. При этом ДЯ/Я~ ВЯ/р^с 1²).

^х) Подстановкой (e^-f-1)^_1 = «интеграл приводится к В-интегралу Эйлера: д ^ (1 —«)'^aM^_'^a du = Г (1 + ia) Г (1 — ta)/T (2) о и по формуле Г (1— г)Г(1+г) = пг/мпяг получается указанный в тексте результат. ²) Эффект осцилляции намагниченности был качественно предсказан Лан­дау (1930). Это явление в металлах называют эффектом де-Гааза~еан-Альфена.

При ВЯ ~ Т амплитуда колебаний магнитного момента ш~ V\iH^l/i (mB)^3/2A~^s. «Монотонная» же часть намагниченности (обозначим ее 9)1), определяющаяся по вычисленной в предыдущем параграфе восприимчивости: 931 ~ Vu.^1/2#/n^3/2B²&^_3. Поэтому

Ш/Ш ~ (ц./8#)^1/2—амплитуда осциллирующей части велика по сравнению с монотонной. Напротив, при ВЯ<^Г эта амплитуда экспоненциально убывает (как ехр (—л^гТфН)) и становится пре­небрежимо малой.

§ 61. Релятивистский вырожденный электронный газ

По мере сжатия газа средняя энергия электронов увеличи­вается (растет г_Р); когда она становится сравнимой с тс², де­лаются существенными релятивистские эффекты. Мы рассмотрим здесь подробно полностью вырожденный ультрарелятивистский электронный газ, энергия частиц которого велика по сравнению с тс². Как известно, в этом случае энергия частицы связана с ее импульсом соотношением

е = ср. (61,1)

Для числа квантовых состояний, а потому и для граничного импульса имеем прежние формулы (57,1—2). Граничная *же энер­гия (т. е. химический потенциал газа) равна теперь

e_f = _Cp_F=(3K²)i/3^^y^/8. (61,2)

Полная энергия газа

или

(61,3)

Давление газа можно получить дифференцированием энергии по объему (при постоянной, равной нулю,— энтропии). Это дает

Давление ультрарелятивистского электронного газа оказывается пропорциональным его плотности в степени 4/3. Необходимо указать, что соотношение

РУ = Т (61,5)

имеет место для ультрарелятивистского газа в действительности не только при абсолютном нуле, но и при всех температурах. В этом легко убедиться в точности тем же способом, каким было

п. V Г ^{83 de} -- ^Е/_К1М

о

Таким образом, для ультра релятивистского ферми-газа дости­гается то предельное значение, которое вообще может иметь (при данном Е) давление какого-либо макроскопического тела (см. § 27). Введя переменную интегрирования e/T = z, напишем:

Q — _ ^VT* Г ^z3dz о

Отсюда видно, что

0 = УГ«/(£). (61,7)

Тем же способом, как это было сделано в § 56, найдем отсюда, что при адиабатическом процессе объем, давление и температура ультрарелятивистского ферми-газа связаны соотношениями

рут ₌ const, VT³ = const, ^ = const. (61,8)

Они совпадают с обычным уравнением адиабаты Пуассона с у = 4/3; подчеркнем, однако, что у отнюдь не является здесь отношением теплоемкостей газа.

Задач и

1. Определить число столкновений со стенкой в ультрарелятивистском
полностью вырожденном электронном газе.

Решение. Вычисление производится так же, как в задаче к § 57, причем надо иметь в виду, что скорость электронов о ж с. В результате получается

Дата добавления: 2014-11-07