Ol — V2X 5 страница

2 2 aw= <&^т 2 (е^^/т 2 е-^Епм'Л = 1.

n п

Отсюда получаем для термодинамического потенциала Q следую­щее выражение:

а = -Г1п2[е^^/г2е-^£«л^1. (35,3)

^г) Это распределение иногда называют большим каноническим.

n

§ 36. Вывод термодинамических соотношений из распределения Гиббса

Распределение Гиббса играет основную роль во всей стати­стике, поэтому изложим здесь еще один способ его обоснования. Это распределение было по существу выведено нами еще в §§ 4 и 6 непосредственно из теоремы Лиувилля. Мы видели, что при­менение теоремы Лиувилля (вместе с соображениями о мульти­пликативности функций распределения подсистем) позволяет сде­лать заключение о том, что логарифм функции распределения подсистемы должен быть линейной функцией ее энергии:

In w_n = а + 6ZT,

(36,1)

причем коэффициенты В одинаковы для всех подсистем данной замкнутой системы (см. (6,4), а в классическом случае—анало­гичное соотношение (4,5)). Отсюда

ш„ = ехр(а + В£„);

если ввести формальным образом обозначения 6 = —1/Г, a —FIT, то это выражение совпадает по форме с распределением Гиббса (31,1). Остается показать, что из самого распределения Гиббса, т. е. чисто статистическим образом, можно вывести основные термодинамиче­ские соотношения.

Мы уже видели, что величина В, а потому и Т, должна быть одинаковой для всех частей находящейся в равновесии системы. Далее, очевидно, что должно быть В < 0, т. е. Т > 0; в противном случае нормировочная сумма Iw_n неизбежно разойдется (поскольку благодаря наличию кинетической энергии частиц энергия Е_п может принимать сколь угодно большие значения). Все эти свойства совпа­дают с основными свойствами термодинамической температуры.

Для вывода же количественного соотношения исходим из усло­вия нормировки

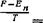
п

Продифференцируем это равенство, рассматривая его левую сто­рону как функцию Т и некоторых величин X_lt %₂, характе­ризующих внешние условия, в которых находится рассматриваемое тело; эти величины могут, например, определять форму и размеры занимаемого телом объема. Уровни энергии Е_п зависят от зна­чений X_lt Х_г,... как от параметров. Производя дифференцирование, пишем:

(для краткости рассматриваем здесь всего один внешний пара­метр к). Отсюда

п п \ п J

В левой стороне равенства 2^=1, ^{а в п}Р^ав°й

п п

(36,2)

Учитывая также, что F—£ = — TS и что¹)

дк ~~ дк '

получаем окончательно

dF = — SdT + ^-dK.

Это и есть общий вид дифференциала свободной энергии.

Таким же образом может быть получено и распределение Гиббса с переменным числом частиц. Если рассматривать число частиц как динамическую переменную, то ясно, что оно тоже будет (для замкнутой системы) «интегралом движения» и к тому же аддитивным. Поэтому надо будет писать:

lnw_nN = a + p'E_n + yN, (36,3)

где у, как и В, должно быть одинаковым для всех частей равно­весной системы. Положив

ОС — у, р — -jT, У ~ f '

получим распределение вида (35,2), после чего тем же способом, как и выше, можно получить выражение для дифференциала по­тенциала й.

¹) Если гамильтониан Я (а с ним и его собственные значения Е_п) зависит от некоторого параметра к, то

дк V дк)_пп

(см. III, (11,16)), откуда после статистического усреднения получается фор­мула (36,2).

ГЛАВА IV

ИДЕАЛЬНЫЙ ГАЗ

§ 37. Распределение Больцмана

Одним из важнейших объектов изучения статистической физики является так называемый идеальный газ. Под этим названием подразумевают газ, взаимодействие между частицами (молекулами) которого настолько слабо, что им можно пренебречь. Физически допустимость такого пренебрежения может быть обеспечена либо малостью взаимодействия частиц при любых расстояниях между ними, либо достаточной разреженностью газа. В последнем, наи­более важном случае разреженность газа приводит к тому, что его молекулы почти всегда находятся на значительных расстоя­ниях друг от друга, на которых силы взаимодействия уже доста­точно малы.

Отсутствие взаимодействия между молекулами позволяет свести квантовомеханическую задачу об определении уровней энергии Е_п всего газа в целом к задаче об определении уровней энергии отдельной молекулы. Эти уровни мы будем обозначать посредст­вом е_А, где индекс k представляет собой совокупность квантовых чисел, определяющих состояние молекулы. Энергии Е_п выразятся тогда в виде сумм энергий каждой из молекул.

Надо, однако, иметь в виду, что даже при отсутствии непосред­ственного силового взаимодействия в квантовой механике имеет место своеобразное взаимное влияние частиц, находящихся в оди­наковом квантовом состоянии (так называемые обменные эффекты). Так, если частицы подчиняются статистике Ферми, то это влияние проявляется в том, что в каждом квантовом состоянии может находиться одновременно не более одной частицы¹); аналогичное влияние, проявляющееся иным образом, имеет место и для частиц, подчиняющихся статистике Бозе.

Обозначим посредством п_к число частиц в газе, находящихся в k-м квантовом состоянии; числа п_к называют числами заполне-

!) Подчеркнем, что, говоря о квантовом состоянии отдельной частицы, мы всегда будем иметь в виду состояния, полностью определенные набором значений всех квантовых чисел (в том числе направлением момента частицы, если она обладает таковым). Их не следует смешивать с квантовыми уровнями энергии—одному и тому же уровню энергии может соответствовать ряд раз­личных квантовых состояний (если уровень вырожден).

ния различных квантовых состояний. Поставим задачу о вычис­лении средних значений n_k этих чисел, причем обратимся к по­дробному изучению чрезвычайно важного случая, когда все числа

n_h<l. (37,1)

Физически этот случай соответствует достаточно разреженному газу. В дальнейшем будет установлен критерий, обеспечивающий выполнение этого условия, но уже сейчас укажем, что факти­чески оно выполняется для всех обычных молекулярных или атомных газов. Это условие нарушилось бы лишь при таких боль­ших плотностях, при которых вещество фактически уже ни в какой мере нельзя было бы рассматривать как идеальный газ.

Условие n_k<^.\ для средних чисел заполнения означает, что в каждый момент времени в каждом квантовом состоянии факти­чески находится не более одной частицы. В связи с этим можно пренебрегать не только непосредственным силовым взаимодейст­вием частиц, но и их косвенным квантовомеханическим взаимным влиянием, упомянутым выше. Это обстоятельство в свою очередь позволяет применить к отдельным молекулам формулу распреде­ления Гиббса.

Действительно, распределение Гиббса было выведено нами для тел, являющихся относительно малыми, но в то же время макро­скопическими частями каких-либо больших замкнутых систем. Макроскопичность тел давала возможность считать их квазизам­кнутыми, т. е. в известном смысле пренебречь их взаимодействием с другими частями системы. В рассматриваемом случае квазизам­кнутыми являются отдельные молекулы газа, хотя они отнюдь не представляют собой макроскопических тел.

Применив к молекулам газа формулу распределения Гиббса, мы можем утверждать, что вероятность молекуле находиться в k-м состоянии, а потому и среднее число n_k молекул в этом состоянии, пропорциональны ехр(—e_k/T):

n_k = ae-^sk/\ (37,2)

где а—постоянная, определяющаяся условием нормировки

2"*=^ (37,3)

(N — полное число частиц в газе). Распределение молекул идеаль­ного газа по различным состояниям, определяемое формулой (37,2), называется распределением Больцмана (оно было открыто Больцманом для классической статистики в 1877 г.).

Постоянный коэффициент в (37,2) может быть выражен через термодинамические величины газа. Для этого дадим еще один вывод этой формулы, основанный на применении распределения

Гиббса к совокупности всех частиц газа, находящихся в данном квантовом состоянии. Мы имеем право сделать это (даже если числа п_к не малы), поскольку непосредственного силового взаи­модействия между этими и остальными частицами (как и между всеми вообще частицами идеального газа) нет, а квантовомеха-нические обменные эффекты имеют место лишь для частиц, нахо­дящихся в одном и том же состоянии. Полагая в общей формуле распределения Гиббса с переменным числом частиц (35,2) Е = п_лг_к, N = n_k и приписывая индекс k величине Q, получим распреде­ление вероятностей различных значений п_к в виде

вд^ехр [°» + ^—₍₃₇₎₄₎

В частности, да₀ = ехр (Q_A/T) есть вероятность полного отсутст­вия частиц в данном состоянии. В интересующем нас здесь случае,

когда п_к<^\, вероятность w₀ близка к единице; поэтому в выра­жении а»! для вероятности наличия одной частицы в k-м состоя­нии можно положить, опуская члены высшего порядка малости, exp(Q_ft/7^,)=l. Тогда

w_t = e ^т.

Что же касается вероятностей значений «_ft>l, то они в том же приближении должны быть положены равными нулю. Поэтому

n_k = '£w_n.n_k = w₁-l,

"ft

и мы получаем распределение Больцмана в виде

n_A = expteS*). (37,5)

Таким образом, коэффициент в формуле (37,2) оказывается выра­женным через химический потенциал газа.

§ 38. Распределение Больцмана в классической статистике

Если бы движение молекул газа (и атомов в них) подчинялось классической механике, мы могли бы ввести вместо распределения по квантовым состояниям распределение молекул по фазовому пространству, т. е. по импульсам и координатам. Пусть dN — сред­нее число молекул, «заключенных» в элементе объема фазового пространства молекулы dpdq = dp_x... dp_rdq_x... dq_r {г — число степеней свободы молекулы). Напишем его в виде

dN = n(p, q) dx, dx = (38,1)

и будем называть п (р, q) плотностью в фазовом пространстве (хотя dx отличается множителем (2п%)~^г от элемента объема фа­зового пространства). Мы получим теперь вместо (37,5)

ехр (³⁸-²)

где г(р, q)—энергия молекулы как функция координат и импуль­сов ее атомов.

Обычно, однако, квазиклассичным оказывается не все движе­ние молекулы, а лишь движение, соответствующее части ее сте­пеней свободы. В частности, в газе, не находящемся во внешнем поле, всегда квазиклассично поступательное движение молекул. При этом кинетическая энергия поступательного движения входит в энергию г_к молекулы как независимое слагаемое, а остальная часть энергии вовсе не содержит координат х, у, г и импульсов Р_х> Р_у< Рг центра инерции молекулы. Это обстоятельство позво­ляет выделить из общей формулы распределения Больцмана мно­житель, определяющий распределение молекул газа по указанным переменным. Распределение молекул по занимаемому газом объему будет, очевидно, просто однородным, а для числа молекул, прихо­дящихся на единицу объема и имеющих импульсы (поступатель­ного движения) в заданных интервалах dp_x, dp_y, dp_z, получим формулу распределения Максвелла

N

V(2nmT)^3/2'

Px + Py + Pz 2тТ

dp_xdp_ydp_z, (38,3)

N f m у'²

m(vx+vy+vD 2Т

dv_xdv_ydv_z (38,4)

(m—масса молекулы), нормированную на N/V частиц в единице объема.

Рассмотрим далее газ, находящийся во внешнем поле, в кото­ром потенциальная энергия молекулы есть функция только от координат ее центра инерции: u = u(x, у, г) (таково, например, гравитационное поле). Если, как это практически всегда имеет место, поступательное движение в этом поле квазиклассично, то и (х, у, г) входит в энергию молекулы в качестве независимого слагаемого. Максвелловское распределение по скоростям молекул остается, разумеется, неизменным, а распределение но коорди­натам центра инерции определится формулой

dN_t = n_ue-^^x-v'*v^t dV. (38,5)

Эта формула дает число молекул в элементе пространственного объема dV — dxdydz; величина же

п(г) = п₀е-^и<^х'У-гУ^т (38,6)

представляет собой плотность числа частиц. Постоянная п₀ есть плотность в точках, где ы = 0. Формула (38,6) называется форму­лой Больцмана.

В частности, в однородном поле тяжести, направленном вдоль оси z, u = mgz, и распределение плотности газа определяется так называемой барометрической формулой

n(z) = n₀e-^m^^T, (38,7)

где п₀—плотность на уровне z = 0.

На больших расстояниях от Земли ее гравитационное поле должно описываться точным ньютоновским выражением, причем потенциальная энергия и обращается на бесконечности в нуль. Согласно формуле (38,6) плотность газа должна была бы иметь при этом на бесконечности отличное от нуля конечное значение. Однако конечное количество газа не может быть распределено по бесконечному объему с нигде не исчезающей плотностью. Это значит, что в гравитационном поле газ (атмосфера) не может на­ходиться в равновесии и должен непрерывно рассеиваться в прост­ранство.

Задачи

1. Найти плотность газа в цилиндре с радиусом R и длиной /, вращаю­щемся вокруг оси с угловой скоростью Q (всего в цилиндре N молекул).

Решение. В §34 было указано, что вращение тела как целого экви­валентно внешнему полю с потенциальной энергией — ¹/₂tnQ²r'ⁱ (г — расстояние до оси вращения). Поэтому плотность газа есть

n(r) = Ae^mQ2r*^/2T.

Нормировка дает

NmQ4^na'^rt'^2T

п (/■)=■

2ягг(^^й2Л2/27-О'

2. Найти распределение частиц по импульсам для релятивистского идеаль­ного газа.

Решение. Энергия релятивистской частицы выражается через ее импульс
посредством е = с ]//?г²с² + р² (с—скорость света). Нормированное распределе-
ние по импульсам есть ________

/ • с Vm²c² + P² N

N_ ^6Хр \ _______ Т)dp_xdp_vdp_z

^d V _п (Т \² /тс²\. Т _v /тс²\ 4л (пк)³ '

где К₀, Ki—функции Макдональда (функции Ганкеля от мнимого аргумента). При вычислении нормировочного интеграла использованы формулы:

V

о

К[ (z) = -±-K₁ (z)-K₀ (2).

§ 39. Столкновения молекул

Молекулы газа, заключенного в сосуде, сталкиваются при своем движении с его стенками. Вычислим среднее число ударов молекул газа об единицу поверхности стенки за единицу времени.

Выберем какой-нибудь элемент поверхности стенки сосуда и вве­дем систему координат с осью г, направленной перпендикулярно к этому элементу поверхности (который можно теперь написать в виде dxdy). Из молекул газа в единицу времени долетят до стенки сосуда, т. е. столкнутся с ней, только те, координаты z которых не больше, чем компонента v_z их скорости по этой оси (которая, конечно, должна к тому же быть направлена к стенке, а не в противоположную сторону).

Число dv_v столкновений молекул в единицу времени (отнесен­ное к единице площади поверхности стенки), при которых компо­ненты скорости лежат в заданных интервалах dv_x, dv_y, dv_z, по­лучится, следовательно, умножением распределения (38,4) на объем цилиндра с основанием 1 см² и высотой, равной v_z. Мы получим тогда

^{dvv =} T(,2nrJ ^{е z}'v_zdv_xdv_ydv_z. (39,1)

Отсюда легко найти полное число v ударов молекул газа об еди­ницу поверхности стенки сосуда в единицу времени. Для этого проинтегрируем (39,1) по всем скоростям v_z от 0 до оо и по v_x и v_v от —оо до +°° (по v_z не надо интегрировать от —оо до О, так как при v_z < 0 молекула летит в сторону, противоположную стенке, и, следовательно, не столкнется с ней). Это дает

*=тУш = уЬ? ⁽³⁹'²⁾

(плотность газа выражена через его давление согласно уравнению Клапейрона).

Формулу (39,1) можно написать в сферических координатах в пространстве скоростей, вводя вместо v_x, v_y, v_z абсолютную величину скорости v и полярные углы 0 и ср, определяющие ее направление. Если выбрать полярную ось по оси г, то v_z = v cos б и

dv_v = -^- ^3/2 ехр ^— Tffrj v³ sin 9 cos 6 dQ dy dv. (39,3)

Рассмотрим теперь столкновения молекул газа друг с другом. Для этого необходимо найти предварительно распределение мо­лекул по их скоростям (скорость есть везде скорость центра инерции) относительно друг друга. При этом мы выбираем какую-нибудь из молекул газа и рассматриваем движение всех остальных молекул относительно этой, т. е. для каждой молекулы ■ мы

(39,5)

Полное число таких столкновений, происходящих в единицу вре­мени во всем объеме газа, равно, очевидно, v'N/2.

Задачи

§ 40. Неравновесный идеальный газ

Распределение Больцмана может быть выведено еще и совсем иным способом, непосредственно из условия максимальности энтропии газа в целом, рассматриваемого как замкнутая система. Этот вывод представляет существенный самостоятельный интерес, поскольку он основан на методе, дающем возможность вычислить энтропию газа, находящегося в произвольном неравновесном макро­скопическом состоянии.

Всякое макроскопическое состояние идеального газа можно характеризовать следующим образом. Распределим все квантовые состояния отдельной частицы газа по группам, каждая из кото­рых содержит близкие состояния (обладающие, в частности, близ­кими энергиями), причем как число состояний в каждой группе, так и число находящихся в них частиц все же очень велики. Перенумеруем эти группы состояний номерами / = 1,2, и пусть Gj есть число состояний в /-й группе, a Nj—число частиц в этих состояниях. Тогда набор чисел N j будет полностью харак­теризовать макроскопическое состояние газа.

Задача о вычислении энтропии газа сводится к задаче об опре­делении статистического веса АГ данного макроскопического состо­яния, т. е. числа микроскопических способов, которыми это состоя­ние может быть осуществлено. Рассматривая каждую группу из N j частиц как независимую систему и обозначая посредством АГ_; ее статистический вес, можем написать:

АГ = Д АГ,,

(40,1)

Таким образом, задача сводится к вычислению ДГ,-.

В статистике Больцмана средние числа заполнения всех кван­товых состояний малы по сравнению с единицей. Это значит, что числа Nj частиц должны быть малы по сравнению с числами Gj состояний (Nj<^.Gj), но, конечно, сами по себе все же очень велики. Как было объяснено в § 37, малость средних чисел заполнения позволяет считать, что все частицы распределяются по различным состояниям совершенно независимо друг от друга. Помещая каждую из N j частиц в одно из G_f состояний, получим всего G^j возможных распределений, среди которых, однако, есть тождественные, отличающиеся лишь перестановкой частиц (час­тицы все одинаковы). Число перестановок N_t частиц есть N_f\, и таким образом, статистический вес распределения Nj частиц по Gj состояниям равен

М\ = ОрЩ/.. (40,2)

Энтропия газа вычисляется как логарифм статистического веса S = ln АГ = 2Ьт ДГ,. Подставив (40,2), имеем

S = S(W/lnG_y—lniV,.!).

i

Имея в виду, что числа N j велики, воспользуемся для InA^I приближенной формулой^х)

lniV! ttN\n(N/e) (40,3)

и получим

S = E^ln|f- (40,4)

Эта формула решает поставленную задачу, определяя энтропию идеального газа, находящегося в произвольном макроскопическом состоянии, определяющемся набором чисел Nj. Перепишем ее, введя средние числа и,- частиц в каждом из квантовых состоя­ний /-й группы: tij = Nj/Gj. Тогда

⁵=H^GA^ln-=-- (⁴⁰>⁵)

Если движение частиц квазиклассично, то в этой формуле можно перейти к распределению частиц по фазовому простран-

¹) При большом Л? можно приближенно заменить сумму lnJV!=lnl-f-

n

+ In 2+... -f-ln N интегралом ^ Inx-dx, откуда и получается (40,3).

о

ству. Разделим фазовое пространство частицы на участки ApV> Aq^{J'\ каждый из которых мал, но содержит все же большое число частиц. Числа квантовых состояний, приходящихся на эти участки, равны

_G a£W! _{= AtV}> ₍4о₎₆₎

^J {2л%У

(г—число степеней свободы частицы), а числа частиц в этих состояниях напишем в виде Nj = n(p, q)Ax^{J\ где п(р, q) — плот­ность распределения частиц в фазовом пространстве. Подставляем эти выражения в (40,5), после чего, имея в виду, что участки Дт⁽/' малы, а их число велико, заменяем суммирование по / интегрированием по всему фазовому пространству частицы:

S = Jnln-^dr. (40,7)

В состоянии равновесия энтропия должна иметь максимальное значение (в применении к идеальному газу это утверждение иногда называют Н-теоремой Больцмана). Покажем, каким образом из этого требования можно найти функцию распределения частиц газа в состоянии статистического равновесия. Задача заключается в нахождении таких tij, при которых сумма (40,5) имеет макси­мальное значение, возможное при дополнительных условиях

2 b^Ni=2 ^fijUj=е,

i i

выражающих постоянство полного числа частиц N и полной энергии Е газа. Следуя известному методу неопределенных мно­жителей Лагранжа, надо приравнять нулю производные

JL(S + aN+№ = 0. (40,8)

Orlj

где а, р — некоторые постоянные. Произведя дифференцирование,

найдем

Gj (— In п_/ + а + 8е_у) = 0, откуда 1пга, = а + 6еу, или

tij = ехр (а + Веу).

Это — не что иное, как известное уже нам распределение Больц­мана, причем постоянные а и р* связаны с Т и ц посредством а = ц/7\ р = -1/7-1).

§ 41. Свободная энергия больцмановского идеального газа

Применим общую формулу (31,3)

F = — Т\п^е~^Еп1^т (41,1)

п

для вычисления свободной энергии идеального газа, подчиняю­щегося статистике Больцмана.

Написав энергию Е„ в виде суммы энергий г_к, мы можем свести суммирование по всем состояниям газа к суммированию по всем состояниям отдельной молекулы. Каждое состояние газа будет определяться набором N (N—число молекул в газе) значе­ний е_к, которые в больцмановском случае можно считать все раз­личными между собой (в каждом молекулярном состоянии—не более одной молекулы). Написав е~^Е"1^т в виде произведения мно­жителей е^_Е*/^г'для каждой из молекул и суммируя независи­мо по всем состояниям каждой молекулы, мы получили бы вы­ражение

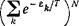
Набор возможных значений e_k для всех молекул газа одинаков, а потому одинаковы и суммы 2^ехР(—4lT)-

Необходимо, однако, иметь в виду следующее обстоятельство. Все наборы N различных значений г_к, отличающиеся лишь рас­пределением одинаковых молекул газа по уровням e_k, соответст­вуют одному и тому же квантовому состоянию газа. В статисти­ческой же сумме в формуле (41,1) каждое из состояний должно учитываться лишь один раз²). Поэтому мы должны еще разде­лить выражение (41,2) на число возможных перестановок N моле­кул друг с другом, т. е. на N1 ³).

Таким образом,

Ze-W-kteeSY. (41,3)

^х) Эти значения а и |5 можно было предвидеть заранее: уравнения (40,8) могут быть записаны в виде соотношения между дифференциалами dS + adN + fidE^O, которое должно совпадать с выражением дифференциала внутренней энергии (при заданном объеме) dE = Т dS-\~ndN. ²) Ср. примечание на стр. 110. ⁸) Существенно, что в статистике Больцмана роль членов, содержащих одинаковые е*, в выражении (41,2) относительно мала.

п \ k J

Подставляя это выражение в (41,1), получаем

F = — TN 1п2е"⁸*^/Г + ^1пЛП

k

Поскольку N—очень большое число, то для 1пЛП можно вос­пользоваться формулой (40,3). В результате получим следующую формулу:

F = -NT\n\^^e-*bl^T, (41,4)

которая позволяет вычислить свободную энергию любого газа, состоящего из одинаковых частиц и подчиняющегося статистике Больцмана.

В классической статистике формула (41,4) должна быть напи­сана в виде

F = — NT\vijj j<r^e<P- Mux, (41,5)

где интегрирование производится по фазовому пространству моле­кулы, a dx определено в (38,1).

§ 42. Уравнение состояния идеального газа

В § 38 уже было отмечено, что поступательное движение моле­кул газа всегда квазиклассично, причем энергию молекулы можно написать в виде

Ч (Р„ Р_У, Рг) = ^Pl+f_m^+pl + ej, (42,1)

где первый член есть кинетическая энергия ее поступательного движения, а посредством г'_к обозначены уровни энергии, соответ­ствующие вращению молекулы и ее внутреннему состоянию; s'_k не зависит ни от скоростей, ни от координат центра инерции молекулы (мы предполагаем, что никакого внешнего поля нет).

Статистическую сумму под знаком логарифма в формуле (41,4) мы должны заменить теперь выражением

?JM-^)5&"-"(&r?'"*'^r <^ед

(интегрирование по dV = dx dy dz производится по всему объему газа V). Для свободной энергии получаем

Г eV (mT -e'Jr'\

F = -NT\n]_[ir{^) £е ^к' ]• (42,3)

Стоящая здесь сумма, разумеется, не может быть вычислена в общем виде, без каких-либо предположений о свойствах молекул.

Существенно, однако, что она представляет собой функцию только от температуры. Поэтому зависимость свободной энергии от объема полностью определяется формулой (42,3), что дает возможность получить из нее ряд существенных общих результатов о свойст­вах идеального газа (не находящегося во внешнем поле).

Выделяя в (42,3) член, содержащий объем, напишем эту фор­мулу в виде

F = -NT\n% + Nf(T), (42,4)

где / (Г) — некоторая функция температуры. Для давления газа получаем отсюда

_р _ d_F_ _ NT dV ~ V '

ИЛИ

PV=NT. (42,5)

Мы получили, таким образом, известное уравнение состояния идеального газа (уравнение Клапейрона). Если температура измеряется в градусах, то¹)

PV=NkT. (42,5а)

Зная F, можно найти также и другие термодинамические вели­чины. Так, термодинамический потенциал равен

ф = — NT\n~- + Nf (T)+PV.

Заменяя V через Р иТ согласно (42,5) (Ф должно быть выражено как функция от Р и Т) и вводя новую функцию температуры X(T) = f(T) — TltiT, получаем

Ф = NT InP + N%(T). (42,6)

Энтропия определяется как

5 = - § = N In -~-Nf (Т) (42,7)

или как функция Р и Т

S = -^d§ = -N\nP-N_t'(T). (42,8)

Наконец, энергия равна

E = F + TS = Nf(T)—NTf'(T). (42,9)

^х) Для грамм-молекулы газа (/V = 6,023 • 10²³—число Авогадро) произве­дение R — Nk называется газовой постоянной:

R = 8,314-Ю⁷ эрг/град.

Мы видим, что энергия является функцией только от температуры газа (то же самое относится и к тепловой функции W = Е + PV= =E + NT). Это обстоятельство, впрочем, заранее очевидно—по­скольку молекулы идеального газа предполагаются не взаимодей­ствующими друг с другом, то изменение их среднего взаимного расстояния при изменении общего объема газа не может сказаться на его энергии.

Дата добавления: 2014-11-07