Ol — V2X 3 страница

так что условие (27,3) переходит в

(х₀ + тф = const,

что совпадает, как и следовало, с (25,2).

Наконец, укажем полезное соотношение, являющееся непосред­ственным следствием условий (27,2) и (27,3). Разделив одно на другое, найдем, что ц/Г = const, откуда следует: d\i/\i = dT/T. С другой стороны, согласно (24,12), при постоянном (равном еди­нице) объеме имеем

dP = SdT + Nd_li,

где S, N—энтропия и число частиц единицы объема тела. Подставляя сюда dT — {Tl\i)d\i и замечая, что цЫ -\-ST ^Ф + БТ= = е-{-Р (е—энергия, отнесенная к единице объема), найдем иско­мое соотношение¹):

^J) В нерелятивистском случае, положив р, я mc², е «рс² ^> Р (р—плот­ность), получим d\i = vdP (v = mjp—объем, отнесенный к одной частице), как и должно было быть при Т= const.

ГЛАВА III

РАСПРЕДЕЛЕНИЕ ГИББСА

§ 28. Распределение Гиббса

Перейдем теперь к поставленной в главе I задаче о нахождении функции распределения для любого макроскопического тела, яв­ляющегося малой частью какой-либо большой замкнутой системы (подсистемой). Наиболее удобный и общий способ подхода к реше­нию этой задачи основан на применении ко всей системе микро­канонического распределения.

Выделим из замкнутой системы интересующее нас тело и будем рассматривать систему как составленную из двух частей: изданного тела и всей остальной ее области, которую мы будем называть по отношению к телу «средой».

Микроканоническое распределение (6,6) напишется в виде

dw = const • б (Е + Е' — E^w) dY dY'

(28,1)

где Е, dY и £", dY' относятся соответственно к телу и среде, a Eⁱ⁰⁾ — заданное значение энергии замкнутой системы; этому значению должна быть равна сумма Е + Е' энергий тела и среды.

Нашей целью является нахождение вероятности w_n такого со­стояния всей системы, при котором данное тело находится в не­котором определенном квантовом состоянии (с энергией Е_п), т. е. в состоянии, описанном микроскопическим образом. Микроскопи­ческим же состоянием среды мы при этом не интересуемся, т. е. будем считать, что она находится в некотором макроскопически описанном состоянии. Пусть АГ' есть статистический вес макроско­пического состояния среды; обозначим также посредством АЕ' интервал значений энергии среды, соответствующий интервалу АГ' квантовых состояний в указанном в § 7 смысле.

Искомую вероятность w_n мы найдем, заменив в (28,1) dY еди­ницей, положив Е — Е_п и проинтегрировав по dY':

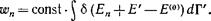
Пусть Г'(£') — полное число квантовых состояний среды с энер­гией, меньшей или равной Е'. Поскольку подынтегральное выра­жение зависит только от Е', можно перейти к интегрированию по dE', написав:

dE

dl"

Производную заменяем (ср. §7) отношением

Л" _e^s'^(£J)

dE'~ АЕ' '

где S' (Е')—энтропия среды как функция ее энергии (функцией £' является, конечно, также и АЕ'). Таким образом,

w,

,, = const. j |fl 6 (£' + Е_п-Е«») dE'.

Благодаря наличию б-фуикции интегрирование сводится к за­мене Е' на £⁽⁰⁾—Е_п, и получаем

w_n = const- (^)_£,_{= £},o,__£n. (28,2)

Учтем теперь, что вследствие малости тела его энергия Е_а мала по сравнению с £⁽⁰'. Величина АЕ' относительно очень мало меняется при незначительном изменении £'; поэтому в ней можно просто положить Е' — £⁽⁰⁾, после чего она превратится в неза­висящую от Е_п постоянную. В экспоненциальном же множи­теле e^s' надо разложить S'(Е^т — £„) по степеням Е„, сохранив также и линейный член:

d£<»>

dS' (£<»>)

S' (£<°>—£„) = S' (£^<0))—£„ -

Но производная от энтропии S' по энергии есть не что иное, как 1/Т, где Т—температура системы (температура тела и среды оди­накова, так как система предполагается находящейся в равно­весии).

Таким образом, получаем окончательно для w_a следующее выражение:

и1_я = Лехр(-£?), (28,3)

где А — не зависящая от £„ нормировочная постоянная. Это — одна из важнейших формул статистики; она определяет статистичес­кое распределение любого макроскопического тела, являющегося сравнительно малой частью некоторой большой замкнутой системы. Распределение (28,3) называется распределением Гиббса ила кано­ническим распределением; оно было открыто Гиббсом (J. W. Gibbs) для классической статистики в 1901 г.

Нормировочная постоянная А определяется условием 2^шп~ откуда

4-= 2 е-*-"¹. (28,4)

Среднее значение любой физической величины /, характеризую­щей данное тело, может быть вычислено с помощью распределе­ния Гиббса по формуле

/ = Z>J_n»= ^П^_е-Е_п/т • (28,5)

п

В классической статистике выражение, в точности соответствую­щее формуле (28,3), получается для функции распределения в фазо­вом пространстве:

р(р, q) = Ае~^Е<Р'Ы^т, (28,6)

где Е(р, q)—энергия тела как функция его координат и импульсов*). Нормировочная постоянная А определяется условием

^pdpdq=A ^t\_je-^EiP'iV^Tdpdq= 1. (28,7)

На практике часто приходится иметь дело со случаями, когда квазиклассическим является не все микроскопическое движение частиц, а лишь движение, соответствующее части степеней сво­боды, в то время как по остальным степеням свободы движение является квантовым (так, например, может быть квазиклассиче­ским поступательное движение молекул при квантовом характере внутримолекулярного движения атомов). В таком случае уровни энергии тела можно написать в виде функций от квазиклассиче­ских координат и импульсов: E_n = E_n(p,q), где п обозначает совокупность квантовых чисел, определяющих «квантовую часть» движения, для которого значения р и q играют роль параметров. Формула распределения Гиббса напишется тогда в виде

dw„(P, q) = Ae-^E_ntP-MTdp_K]1dq_K]I, (28,8)

где dp_Kadq_K1I—произведение дифференциалов «квазиклассических» координат и импульсов.

*) Во избежание недоразумений лишний раз напомним, что w_n (или р) являются монотонными функциями энергии и отнюдь не должны иметь ма­ксимума при Е = Е. Острый максимум при Е = Е имеет функция распределе­ния по энергии, получающаяся умножением w_n на dY (E)/dE.

Наконец, необходимо сделать следующее замечание по поводу круга вопросов, для решения которых можно применять распреде­ление Гиббса. Мы все время говорили о последнем как о статис­тическом распределении для подсистемы, каковым оно в действи­тельности и является. Весьма важно, однако, что это же распре­деление можно с полным успехом применять и для определения основных статистических свойств замкнутых тел. Действительно, такие свойства тела, как значения его термодинамических вели­чин или распределения вероятностей для координат и скоростей отдельных его частиц, очевидно, не зависят от, того, рассматри­ваем ли мы тело как замкнутое или как помещенное в воображае­мый термостат (§7). В последнем случае, однако, тело становится «подсистемой» и распределение Гиббса применимо к нему бук­вально. Отличие замкнутого тела от незамкнутого проявляется при применении распределения Гиббса по существу лишь при рассмотрении сравнительно мало интересного вопроса о флуктуа-циях полной энергии тела. Распределение Гиббса дает для сред­ней флуктуации этой величины отличное от нуля значение, кото­рое для тела, находящегося в среде, имеет реальный смысл, а для замкнутого тела—совершенно фиктивно, так как энергия такого тела по определению постоянна и не флуктуирует.

Возможность применения (в указанном смысле) распределения Гиббса к замкнутым телам видна также и из того, что оно по существу очень слабо отличается от микроканонического (и в то же время несравненно удобнее для проведения конкретных расче­тов). Действительно, микроканоническое распределение эквива,-лентно, грубо говоря, признанию равновероятными всех микро­состояний тела, отвечающих заданному значению его энергии. Каноническое же распределение «размазано» по некоторому ин­тервалу значений энергии, ширина которого (порядка величины средней флуктуации энергии), однако, для макроскопического тела ничтожно мала.

§ 29. Распределение Максвелла

Энергия Е(р, q) в формуле распределения Гиббса классической статистики всегда может быть представлена как сумма двух частей — кинетической и потенциальной энергий. Из них первая есть квадратичная функция от импульсов атомов¹), а вторая—функ­ция от их координат, причем вид этой функции зависит от закона взаимодействия частиц внутри тела (и от внешнего поля, если таковое имеется). Если кинетическую и потенциальные энергии обозначить соответственно как К (р) и U (q), то Е (р, q) — =К{р) + и (я), и вероятность dw = p(p, q)dpdq напишется в виде

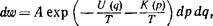
*) Предполагается, что мы пользуемся декартовыми координатами.

т. е. разбивается на произведение двух множителей, из которых один зависит только от координат, а другой—только от импуль­сов. Это означает, что вероятности для импульсов и координат независимы друг от друга в том смысле, что определенные зна­чения импульсов никак не влияют на вероятности тех или иных значений координат, и обратно. Таким образом, вероятность раз­личных значений импульсов может быть написана в виде

dw_p = ae-KM'^Tdp, (29,1)

а распределение вероятности для координат

dw_g=be-^u^)/Tdq. (29,2)

Так как сумма вероятностей всех возможных значений импуль­сов (и то же самое для координат) должна быть равна единице, то каждая из вероятностей dw_p и dw_g должна быть нормирована, т. е. их интегралы по всем возможным для данного тела значе­ниям импульсов или координат должны быть равны единице. Из этих условий можно определить постоянные а и b в (29,1) и (29,2).

Займемся изучением распределения вероятностей для импуль­сов, еще раз подчеркнув при этом весьма существенный факт, что в классической статистике такое распределение нисколько не зависит от рода взаимодействия частиц внутри системы или от рода внешнего поля и потому распределение может быть выражено в виде, пригодном для любых тел¹).

Кинетическая энергия всего тела равна сумме кинетических энергий каждого из входящих в него атомов, и вероятность опять разбивается на произведение множителей, из которых каждый зависит от импульсов только одного из атомов. Это вновь озна­чает, что вероятности импульсов различных атомов не зависят друг от друга, т. е. импульс одного из них никак не влияет на вероятности импульсов всех других. Поэтому можно писать рас­пределение вероятностей для импульсов каждого атома в отдель­ности.

Для атома с массой т кинетическая энергия равна (pl + Pl + pt)/2m, где р_х, р_у, р_г—декартовы составляющие его импульса, а распределение вероятностей имеет вид

dw^ae~^^{(vl +Р}" dp_xdp_ydp_z.

Постоянная а определяется условием нормировки. Интегрирова­ния по dp_x, dp_y, dp_z разделяются и производятся с помощью известной формулы

*) В квантовой статистике это утверждение, вообще говоря, не справедливо.

§ e~^ax'dx

В результате находим а = (2лтТ)-^3/2, и мы получаем оконча­тельное распределение вероятностей для импульсов в виде

<Ч = 7£^Г ^еХР (- ^Pl+2mT^+Pl) ^dP*^dPy^dP*- (29.3)

(2nmT)^3,i Ч ^2mT

Переходя от импульсов к скоростям (p = mv), можно написать аналогичное распределение для скоростей:

^v = (₂-^)^3/2exp ]dv_xdv_¥dv.. (29,4)

Это—так называемое распределение Максвелла (J. С. Maxwell, 1860 г.). Заметим, что оно снова распадается на произведение трех независимых множителей:

dwo^yf&e-** (29,5)

каждый из которых определяет распределение вероятностей для отдельной компоненты скорости.

Если тело состоит из молекул (например, многоатомный газ), то наряду с распределением Максвелла для отдельных атомов такое же распределение имеет место и для поступательного дви­жения молекул как целых. Действительно, из кинетической энер­гии молекулы можно выделить в виде слагаемого энергию посту­пательного движения, в результате чего искомое распределение выделится в виде выражения (29,4), в котором под m надо будет понимать полную массу молекулы, а под v_x, v_y, v_z—компоненты скорости ее центра инерции. Подчеркнем, что распределение Мак­свелла для поступательного движения молекул может иметь место вне зависимости от характера внутримолекулярного движения атомов (и вращения молекулы), в том числе и в случае, когда последнее должно описываться квантовым образом^г).

Выражение (29,4) написано в декартовых координатах в «про­странстве скоростей». Если от декартовых координат перейти к сферическим, то получится

^dWv= (-^)^3/* е^-mv°^/2T v² siriQ-dedy dv, (29,6)

где v—абсолютная величина скорости, абиф—полярный угол и азимут, определяющие направление скорости. Интегрируя по уг­лам, найдем распределение вероятностей для абсолютной вели­чины скорости

*) Распределение Максвелла справедливо, очевидно, и для так называемого орауновского движения взвешенных в жидкости частиц.

dw_v = 4л (J^j^3/2 е-™'/2г _V2 _dv, (29,7)

Иногда бывает удобно пользоваться цилиндрическими коорди­натами в пространстве скоростей. Тогда

^dw* = (шг) ^ехР [------------------------- 1г—

v_rdv_rdv_zdy, (29,8)

где v_z—компонента скорости по оси г, v_r—-перпендикулярная к оси г компонента скорости, а ср—угол, определяющий направ-. ление последней.

Вычислим среднее значение кинетической энергии атома. Со­гласно определению средних значений и пользуясь (29,5), нахо­дим для любой декартовой компоненты скорости ^х)

___ +»

% = Y^T1v%e-™%*4v_x=^. (29,9)

— со

Поэтому среднее значение кинетической энергии атома равно 3772. Можно, следовательно, сказать, что средняя кинетическая энер­гия всех частиц тела в классической статистике всегда равна 3NT/2, где N — полное число частиц.

*) Приведем для справок значения часто встречающихся при применениях распределения Максвелла интегралов вида

/_п=^ е'**' x»dx. о

Подстановка ах² = у дает

где Т (х)—гамма-функция. В частности, если п — 2г, г > 0, то

г (^2г~¹)^!! л/^г~^^г

'ал— 27 + 1 у _а2г+1> где (2г —1)11 = 1-3-5... (2г — 1). Если г = 0, то

Если же п = 2г-\-\, то

Тот же интеграл в пределах от — оо до + оо равен в последнем случае нулю, а в первых двух — удвоенному интегралу от 0 до оо.

Задачи

1. Найти среднее значение п-й степени абсолютной величины скорости. Решение. Пользуясь (29,7), находим

о

В частности, если п — четное число (п = 2г), то

<v*r> = ^Y (2г+Щ

Если же n = 2r-\-l_f то

У л \ т)

2. Найти средний квадрат флуктуации скорости.

Решение. Пользуясь результатом задачи 1 для я=1 и я = 2, находим <(Ati)^a>=F²—1!²=— (з—-

m \ я

3. Найти среднюю энергию, средний квадрат энергии и средний квадрат
флуктуации кинетической энергии атома.

Решение. Пользуясь результатами задачи ], находим

4. Найти распределение вероятностей для кинетической энергии атома.
Решение.

в

2 ~ — dw_z = —7=4 ^Т V~sde.

уИт⁵

5. Найти распределение вероятностей для угловых скоростей вращения
молекул.

Решение. По тем же причинам, что и для поступательного движения, можно писать (в классической статистике) распределение вероятностей для вращения каждой молекулы в отдельности. Кинетическая энергия вращения молекулы, рассматриваемой как твердое тело (что возможно в силу малости внутримолекулярных колебаний атомов), равна

е_вр = у (/1^1+^2 +/з"з)== у \7₁~^^r~T₂~^^r~f₃~

где /j, /₂, /₃—главные моменты инерции, Q_lt Q₂, Q₃—проекции угловой скорости на главные оси инерции, a /W₁ = /₁Q₁, M₂ = 1₂Q₂, M₃ = /₃Q_S—ком­поненты момента вращения, играющие роль обобщенных импульсов для ско­ростей fij, Q₂> йа- Нормированное распределение вероятностей для компонент момента есть

dw_fA = (2nT)~ ² (/xVaf ² е~ ^гГ Wi ⁺ Л ⁺ / dM_xdM₂dM₃,

а для угловой скорости

dw_Q = (2nT) ² (/_х/₂/₃)² е ^{iT V} 'dQ₁dQ_idQ₃.

6. Найти средние квадраты абсолютной величины угловой скорости и мо­мента вращения молекулы.

Решение. С помощью найденных распределений получим

<Q*> =Г (±+±+-^1, <л*2>^Г(/₁ + /₂+/₃).

§ 30. Распределение вероятностей для осциллятора

Рассмотрим тело, атомы которого совершают малые колебания относительно некоторых положений равновесия. Речь может идти о колебаниях атомов кристалла или о колебаниях атомов в мо­лекулах газа (в последнем случае движение молекулы как целого не влияет на колебания атомов в ней и не сказывается на ре­зультатах).

Как известно из механики, функция Гамильтона (энергия) системы, состоящей из произвольного числа частиц, совершающих малые колебания, может быть представлена в виде суммы

а

где q_a— так называемые нормальные координаты колебаний (вточ­ках равновесия q_a = 0), р_а = q_a—соответствующие им обобщенные импульсы, а со_а—частоты колебаний. Другими словами, Е(р, q) распадается на сумму независимых членов, каждый из которых соответствует отдельному нормальному колебанию (или, как го­ворят, осциллятору). В квантовой механике то же самое имеет место для оператора Гамильтона системы, так что каждый осцил­лятор квантуется независимо, и уровни энергии системы пред­ставляются суммами

а

(п_а—целые числа).

В силу этих обстоятельств распределение Гиббса для системы в целом распадается на произведение независимых множителей, каждый из которых определяет статистическое распределение для отдельного осциллятора. На этом основании мы рассматриваем ниже отдельный осциллятор.

¹) Нормальная координата q имеет размерность см-г^'.

Определим распределение вероятностей для координаты q ос­циллятора¹) (индекс а, указывающий номер осциллятора, в даль­нейшем везде опускаем). В классической статистике этот вопрос решался бы совсем просто: поскольку потенциальная энергия осциллятора есть Va®²?², ^т0 распределение вероятностей дается формулой

(Uug^Ae-^'i'^dq, или, определяя А из условия нормировки,

dw_t=j2=re-"<™dq (30,1)

(интегрирование по dq можно производить ввиду быстрой сходи­мости интеграла в пределах от — оо до + оо).

Обратимся к решению поставленной задачи в квантовом слу­чае. Пусть т|>„(<7)—волновые функции стационарных состояний осциллятора, соответствующие уровням энергии

Если осциллятор находится в п-и состоянии, то квантовоме-ханическое распределение вероятностей для его координаты опре­деляется квадратом г|>Ц (в данном случае функции i|>„ вещественны, и поэтому мы пишем просто яр£ вместо квадрата модуля |гр_в|^а). Искомое статистическое распределение вероятностей получится, если умножить на вероятность w_n найти осциллятор в п-м состоянии, а затем суммировать по всем возможным состояниям.

Согласно распределению Гиббса w„ имеет вид

w_a = ae~^e"^IT,

где а—постоянная. Таким образом, получаем формулу

«

dw. = adq 2 е"^е«^/Г ЧЯ, (30,2)

п=0

которая находится, разумеется, в полном соответствии с общей формулой (5,8).

Для вычисления стоящей здесь суммы можно применить сле­дующий прием. Вводим обозначение dw_q = p_ndq и составляем про­изводную

Введя оператор импульса р = — ihdjdq и помня, что импульс осциллятора имеет отличные от нуля матричные элементы лишь для переходов с п—+п± 1 (см. III, § 23), пишем:

(0

= £ (?»-!, пЪп-1 — Яа + Ь Л +

(использованы соотношения

Ри-1, п = — "°<7л-1, п. Pn+L п = "°<7л + 1, п

между матричными элементами импульса и координаты). Таким образом, имеем

В первой сумме меняем обозначение индекса суммирования (п—*-—► л-f-l) и, принимая во внимание соотношения

находим

Аналогичным образом найдем равенство

сс

др, = а(1+е-^/⁷') 2?_я,_{в + 1}1М>_в+хе-^е»>^г.

л = 0

Сравнив оба равенства, получим уравнение откуда

p_e = const-ехр(— а^г J th^

Определяя постоянную из условия нормировки, получим окон­чательно следующую формулу (F. Block, 1932):

^=(i^th|)"'^exp(-'^,f^thi?)^d'- <^

Таким образом, и в квантовом случае вероятности различных значений координаты осциллятора распределены по закону вида ехр(—Ш7²), но с другим по сравнению с классической статисти­кой значением коэффициента а. В предельном случае %ы<^Т, когда квантование уже не играет роли, формула (30,3), как и следовало, переходит в (30,1).

В обратном предельном случае fm^>T формула (30,3) пере­ходит в т. е. в чисто квантовое распределение вероятностей координаты в нормальном состоянии осциллятора¹). Это соответствует тому, что при Т <^Дсо колебания осциллятора практически не воз­буждены.

Распределение вероятностей для импульса осциллятора можно написать по аналогии с (30,3), не проводя вычислений заново. Дело в том, что задача о квантовании осциллятора полностью симметрична в отношении координаты и импульса, и волновые функции осциллятора в р-представлении совпадают с его обыч­ными координатными волновыми функциями (с заменой q на р/со; см. III, § 23, задача 1). Поэтому искомое распределение есть

В классическом предельном случае (fm <<; Т) оно переходит в обыч­ное распределение Максвелла

dw_p=(2nT)-^e-P'^/2Tdp. (30,5)

Задача

Определить координатную матрицу плотности гармонического осцил­лятора.

Решение. Координатная матрица плотности осциллятора, отвечающая статистическому равновесию, определяется формулой

p(M')="i;«"⁸"\(«')i(?)

я = 0

(ср. примечание на стр. 31). Положим q = r-\-s, q'—r— s и вычислим про­изводную (dp/ds)_r. Подобно аналогичному вычислению в тексте, получим

*₌*-jE. ₌ _^ (l _{+ e}-Wr)v q_n,_{n + l}l^_n+imn(q')-^(q)^ _{+ 1}(q')].
ds dq dq % ^

U)r-^spT^cth-

Вычислив таким же образом величину sp = (q—q')p/2 и сравнив с найденной производной, получим

па

откуда

Функция A(r) определяется требованием, чтобы при s=0, т. е. q = q' = r «диагональные элементы» матрицы плотности р (q, q) совпадали с (30,3). Окон­чательно:

, п / ю _1U»Cd\i/! (co(g + 9')²., йсо u>(q—q')²,, ha> \

!) Это есть квадрат модуля волновой функции нормального состояния осциллятора.

§ 31. Свободная энергия в распределении Гиббса

Согласно формуле (7,9) энтропия тела может быть вычислена как среднее значение логарифма его функции распределения:

S = — <\nw_n>. Подставив сюда распределение Гиббса (28,3), получим

S = — In Л + у-,

откуда \пА=(Е— TS)JT. Но средняя энергия Е есть как раз то, что понимается под энергией в термодинамике, поэтому Е—TS = F и In A = F/T, т. е. нормировочная постоянная распре­деления непосредственно связана со свободной энергией тела. Таким образом, распределение Гиббса можно написать в виде

^ = ехр(^=^), (31,1)

F-E(p, q)

(31,2)

в котором оно наиболее часто и применяется. Тем же способом получим в классическом случае с помощью (7,12) выражение

p = (2nh)~³ ехр

Условие нормировки для распределения (31,1) гласит:

2ш„ = е^2^^£»^/Г = 1,

п п

ИЛИ

р = _Г1п2е^-£"^/Г. (31,3)

п

Эта формула является основой для термодинамических примене­ний распределения Гиббса. Она дает в принципе возможность вычислить термодинамические функции любого тела, если известен его энергетический спектр.

Стоящую в (31,3) под знаком логарифма сумму обычно назы­вают статистической суммой. Она представляет собой не что иное, как след оператора ехр(—HIT), где Н — гамильтониан данного тела¹):

Z = 2e~^£"^/r=Sp(e-^^T). (31,4)

п

Такая форма записи обладает тем преимуществом, что для вы­числения следа можно пользоваться любой полной системой вол­новых функций.

^х) В соответствии с общими правилами под ехр (—Н/Т) понимается опе­ратор, собственные функции которого совпадают с собственными функциями оператора Н, а собственные значения равны ехр (—Е_п/Т).

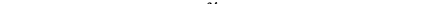
интеграла в действительности сводится к задаче об интегрирова­нии функции ехр [— U (q),'T] по координатам.

При фактическом вычислении статистического интеграла обычно бывает удобным расширить область интегрирования, вводя при этом соответствующий поправочный множитель. Пусть, например, речь идет о газе, состоящем из N одинаковых атомов. Тогда можно производить интегрирование по координатам каждого атома независимо, распространив интегрирование по всему занимаемому газом объему; результат, однако, надо будет разделить на число возможных перестановок N атомов, т. е. на N1 Другими словами,

интеграл j можно заменить деленным на ЛП интегралом по всему фазовому пространству:

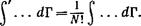
(31,7)

Аналогичным образом удобно расширить область интегриро­вания для газа, состоящего из N одинаковых молекул: по коор­динатам молекул как целых (по координатам их центров инерции) интегрируем независимо по всему объему, а по внутримолекуляр­ным координатам атомов — в каждой молекуле по ее собственному «объему» (т. е. по небольшой области, в которой могут еще с за­метной вероятностью находиться составляющие молекулу атомы); после этого интеграл снова должен быть поделен на N1

Задачи

1. Потенциальная энергия взаимодействия частиц тела есть однородная функция л-го порядка от их координат. Воспользовавшись соображениями подобия, определить, какой вид должна иметь свободная энергия такого тела в классической статистике.

Решение. В статистическом интеграле

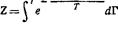
Дата добавления: 2014-11-07