Ol — V2X 1 страница

D (Л

Dx dy

О (У)

In

Р

V-i

I-v

ДУ

■ Т

т \ дТ

\dv)_T дЕ

т' \дР)т ^V I dW\

= C_V + V

,+<

^f dV \

dTj_P' \дТ J_v

(#),-^с'-'(

(16,5)

(16,6)

,(16,7) (16,8)

Наконец, покажем, каким образом можно вычислить тепло­емкость С₀ по теплоемкости С_р и уравнению состояния, пользуясь в качестве основных переменными Т, Р. Поскольку C_V = T (dS/dT)_v, то речь идет здесь о преобразовании производной (dS/dT)_v к дру­гим независимым переменным. Такого рода преобразование проще всего осуществляется с помощью якобианов^х).

dS_\ fdV\ дТ)_Р\дР)_т-

(dS\ fdV\ \дР)_т\дт)_{Р =}

Пишем:

d(S, V)

,д(Т, Р)

V) д (Г, V) ' д (Т, Р)

(дУ \дР

Г -т(^дА\ _Td(S,V)__n ¹ \dTJv д(Т,

— Со—т

дУ_ дТ

\дР)_т

^г) Якобианом

д(и, у) д(х, у)

называют определитель

д (и, у) д(х, у)'

ди ди

дх ду

dv dv

дх ду

Он обладает следующими очевидными свойствами:

d(v, и) __ д (и, у)

д(х, у)~~~д(х, у)' д(и, у) _Гди\ д(х, у) \дх)у'

Далее имеют место следующие соотношения:

д (и, у)д (и, v) d(t, s)

du \ ------- V 1 dt';

д(х, у) d(t, s) д(х, у)'

d д (и, v) _

dt д(х, у) д(х, у) ^ д(х, у)

(II) (III)

(IV) (V)

Подставляя сюда (16,4), получим искомую формулу

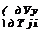
dV\ dp)l

С_р-С„ = -Т^У±. (16,9)

р

Аналогичным образом, преобразуя С_р = Т [-^г]^ к перемен-

ным Т, V, можно получить формулу

дР

с_р-с„=-т^Щ^-. (1б,ю)

[W)_T

Производная (dP/dV)_T всегда отрицательна—при изотермиче­ском расширении тела его давление всегда падает (в § 21 это обстоятельство будет доказано строго). Из формулы (16,10) сле­дует поэтому, что для всех тел

C_p>C_v. (16,11)

При адиабатическом расширении (или сжатии) тела остается неизменной его энтропия. Поэтому связь между температурой, объемом и давлением тела при адиабатическом процессе определяет­ся различными производными, взятыми при постоянной энтропии. Выведем формулы, позволяющие вычислить эти производные по уравнению состояния тела и его теплоемкости.

Для производной от температуры по объему имеем, переходя к независимым переменным V, Т:

д (Т, S) /(5S^

дТ\ д(Т, S) _ d(V, Т) ___ \дУ)_т _____ Т_ [ dS\

dV)s~d(V, S)~ d{V, S) ~ (dS\ ~ C_v[dVj_T>
d(V, T) \&r)y

или, подставляя (16,3):

(£).--£(Я- <¹⁶'^l2>

Аналогичным образом найдем формулу

(£).Ч(Я- <»•»>

*) В § 21 будет доказано строго, что всегда C_v > 0, а потому и С_р > 0.

Из этих формул видно, что если коэффициент теплового рас­ширения (dV/oT)_P положителен (отрицателен), то при адиабати­ческом расширении температура тела падает (возрастает)^х).

Далее, вычислим адиабатическую сжимаемость тела. Пишем:

д (У, S) (dS\

(дУ \ ₌ д (У, S) _ д (У, Т) д(У,Т) _ \дТ)у /дУ\ [дР J_s~d(P, S)~ d(P, S) d(P, Т) — fdS\ \dPj_T'

д(Р.Т) [дТ]_Р

или

dPJs С_р\дР)_т' I¹⁰'¹*'

Ввиду неравенства С_р > C_v отсюда следует, что адиабатическая сжимаемость по абсолютной величине всегда меньше изотерми­ческой сжимаемости.

Используя формулы (16,9—10), можно получить из (16,14) соотношения

§ 17. Термодинамическая шкала температуры

Покажем, каким образом можно, по крайней мере в принципе, построить термодинамическую шкалу температуры, используя для этого произвольное тело, уравнение состояния которого заранее не предполагается известным. Другими словами, задача состоит в том, чтобы с помощью этого тела установить зависимость Т — Т(х) между абсолютной шкалой температуры Т и некоторой чисто условной шкалой т, определяемой произвольно градуиро­ванным «термометром».

Для этого исходим из следующего соотношения (все величины относятся к данному телу):

Ш\ -т(Ё1\ _т(™\

дР]_т \dPJr~~ ¹\дТ)р

(мы использовали (16,4)). Поскольку т и Т связаны друг с дру­гом взаимно однозначно, то безразлично—писать ли производную

при постоянном Т или т. Производную же {^f^j переписываем

в виде

[дт)_Р \ дт Jp dT •

Тогда имеем

dQ \ гр (дУ \ dx

ИЛИ

dx

(17,1)

В правой стороне равенства стоят величины, которые могут быть непосредственно измерены как функции условной темпера­туры т: (dQ/dP)_x определяется количеством тепла, которое должно быть сообщено телу для того, чтобы при расширении поддержать его температуру постоянной, а производная (дУ/дт)_р определяется изменением объема тела при нагревании. Таким образом, формула (17,1) решает поставленную задачу, позволяя определить искомую зависимость Г = Г(т).

При этом надо иметь в виду, что интегрирование соотноше­ния (17,1) определяет In Г с точностью до аддитивной постоянной. Отсюда сама температура Т определится с точностью до произ­вольного постоянного множителя. Разумеется, так и должно быть—выбор единиц измерения абсолютной температуры остается произвольным, что эквивалентно наличию произвольного мно­жителя в зависимости Т — Т (т).

§ 18. Процесс Джоуля — Томсона

Рассмотрим процесс, заключающийся в том, что газ (или жид­кость), находящийся под давлением P_lt стационарным образом переводится в сосуд, где его давление есть Р_г. Стационарность

процесса означает, что в продол­жение всего процесса давления Р_х и Р₂ остаются постоянными. ' Такой процесс можно схематически представить как переход газа че­рез пористую перегородку (а на рис. 2), причем постоянство дав­лений по обе стороны перегородки поддерживается соответственно вдвигающимся и выдвигающим­ся поршнями. Если отверстия в перегородке достаточно малы, то скорость макроскопического течения газа можно считать равной нулю. Будем также предполагать, что газ теплоизолиро­ван от внешней среды.

Описанный процесс называется процессом Джоуля—Томсона. Подчеркнем, что этот процесс необратим, что видно уже из нали­чия перегородки с маленькими отверстиями, которая создает большое трение, уничтожающее скорость газа.

Пусть некоторое количество газа, занимавшее при давлении Р_х объем V_lt переходит (теплоизолированно) в объем У₂, причем давление становится равным Р₂. Изменение энергии £₂— Е_г этого

газа будет равно работе, произведенной над газом для того, чтобы вытеснить его из объема V_x (эта работа равна PjVj), минус та работа, которая производится самим газом для того, чтобы занять объем У₂ при давлении Р₂ (эта работа равна P₂V₂). Таким образом, имеем: Е₂ — £_х = Р-У_г—P₂V₂, т. е. E₁ + P₁V_l = E_i + P_iV_s или

W_t=W₂. (18,1)

Таким образом, при процессе Джоуля — Томсона сохраняется тепловая функция газа.

Изменение температуры при малом изменении давления в ре­зультате процесса Джоуля — Томсона определяется производ­ной дТ/дР, взятой при постоянной тепловой функции. Преобра­зуем эту производную, переходя к независимым переменным Р, Т. Имеем

д(Т, W) (dW\
'дТ\ __д(Т, W) _ д (Р, Т) \дР)_т

dPj_w д(Р, W) д(Р, W) (^dw\

д(Р, Т) \дТ I,

Т[^А -V]. (18,2)

откуда с помощью формул (14,7) и (16,7) получаем

\dPJv C^L \дТ j_P

Изменение энтропии определяется производной (dS/dP)_w. Из соотношения dW = TdS -\-VdP, написанного в виде dS = = dW/T—VdP/T, имеем

^/dS'^V(18,3)

.dPJw T

Эта величина всегда отрицательна, как и должно было быть: переход газа к меньшему давлению путем необратимого процесса Джоуля—Томсона сопровождается увеличением энтропии.

Скажем несколько слов о процессе, заключающемся в том, что газ, первоначально находившийся в одном из двух сообщаю­щихся сосудов, расширяется во второй сосуд; этот процесс, ра­зумеется, не стационарен, и давления в обоих сосудах меняются, пока не сравняются друг с другом. При таком расширении газа в пустоту сохраняется его энергия Е. Если в результате расши­рения общий объем меняется лишь незначительно, то изменение

температуры определяется производной (j^J. • Переходя в этой

(18,4)

•^г(а:

производной к независимым переменным V, Т, получим формулу

(-) =-\dVj_E с

Для изменения энтропии имеем

Как и следовало, энтропия возрастает при расширении.

§ 19. Максимальная работа

Рассмотрим теплоизолированную систему, состоящую из не­скольких тел, не находящихся друг с другом в тепловом равно­весии. В течение процесса установления равновесия система может совершать работу (над какими-либо внешними объектами). Переход в равновесие может, однако, совершаться различным образом, причем будут различными и окончательные равновесные состояния системы; в частности, будут различными ее энергия и энтропия.

Соответственно этому полная работа, которую можно получить от неравновесной системы, будет зависеть от способа установле­ния равновесия, и можно поставить вопрос о том, каким образом должен произойти переход в равновесное состояние, для того чтобы система произвела наибольшую возможную работу. При этом мы интересуемся именно той работой, которая производится за счет неравновесности системы; это значит, что надо исключить работу, которая могла бы быть произведена за счет общего рас­ширения системы,— такая работа могла бы производиться и си­стемой, находящейся самой по себе в равновесии. Соответственно этому будем предполагать, что в результате процесса общий объем системы остается неизменным (хотя и может меняться в течение процесса).

Пусть первоначальная энергия системы есть Е₀, а энергия в состоянии равновесия как функция от энтропии системы в этом состоянии Е (5). Вследствие теплоизолированное™ системы про­изведенная ею работа равна просто изменению энергии:

\R\ = E₀-E(S)

(мы пишем | R |, так как по принятому нами условию R < 0, если работа производится самой системой).

Дифференцируя | R | по энтропии S конечного состояния, имеем

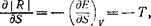
где Т—температура конечного состояния; производная берется при заданном значении объема системы в конечном состоянии (совпадающем с его начальной величиной). Мы видим, что эта производная отрицательна, т. е. | R | уменьшается с увеличением S. Но энтропия теплоизолированной системы не может убывать. Поэтому наибольшее возможное | R | будет достигнуто, если S останется в течение всего процесса неизменной.

Таким образом, мы приходим к выводу, что система произ­водит максимальную работу в том случае, когда ее энтропия остается постоянной, т. е. переход в равновесное состояние со­вершается обратимым образом.

Определим максимальную работу, которая может быть произ­ведена при обмене малым количеством энергии между двумя

телами с различными температурами 7\ и Т₂; пусть Т₂ > 7\. Прежде всего подчеркнем, что если бы передача энергии проис­ходила непосредственно при соприкосновении обоих тел, то никакой работы вообще не было бы произведено. Процесс был бы необратимым (энтропия обоих тел увеличилась бы на б£(1/Т₁—1/Г₂), где 8Е — перенесенное количество энергии).

Поэтому для того, чтобы осуществить обратимый перенос энергии и, соответственно, получить максимальную работу, необ­ходимо ввести в систему еще одно вспомогательное тело (рабочее тело), совершающее определенный обратимый круговой процесс. Процесс этот должен осуществляться таким образом, чтобы тела, между которыми происходит непосредственный обмен энергией, находились при одинаковой температуре. Именно, рабочее тело при температуре Т₂ приводится в соприкосновение с телом с тем­пературой Т₂ и изотермически получает от него определенную энергию. Затем оно адиабатически охлаждается до температуры 7\, отдает при этой температуре энергию телу с температурой 7\ и, наконец, адиабатически возвращается в первоначальное состояние. При расширениях, связанных с этим процессом, рабочее тело производит работу над внешними объектами. Описанный круговой процесс называется циклом Карт.

Переходя к вычислению получающейся максимальной работы, замечаем, что рабочее тело можно при этом не рассматривать, поскольку оно возвращается в результате процесса в исходное состояние. Пусть более нагретое второе тело теряет количество энергии —8Е₂ =— T₂8S₂, а первое получает при этом энергию 8E_l = T₁8S_v Ввиду обратимости процесса сумма энтропии обоих тел остается постоянной, т. е. 8S_X =— 8S₂. Произведенная работа равна уменьшению полной энергии обоих тел, т. е.

I S# Imax = - 8Е₁-8Е₂ = - T.8S, - T₂8S₂ = -{T_t- 7\) 6S₂,

или

|WU = ^^i|S£₂|. (19,1)

Отношение совершенной работы к количеству затраченной энергии называют коэффициентом полезного действия ц. Макси­мальный коэффициент полезного действия при переходе энергии от более нагретого к менее нагретому телу равен, согласно (19,1),

4».x=^z:t¹^. (ад

* 2

Более удобной величиной является коэффициент использования п, определяемый как отношение произведенной работы к максималь­ной работе, которая может быть получена в данных условиях. Очевидно, что n = r\/r\_max.

§ 20. Максимальная работа, производимая телом, находящимся во внешней среде

Рассмотрим теперь вопрос о максимальной работе в другой постановке. Пусть тело находится во внешней среде, причем температура Т₀ и давление Р₀ среды отличны от температуры Т и давления Р тела. Тело может совершать работу над некоторым объектом, который предполагается теплоизолированным как от среды, так и от данного тела. Среда вместе с находящимися в ней телом и объектом работы образует замкнутую систему. Среда обладает настолько большими объемом и энергией, что изменение этих величин в результате происходящих с телом процессов не приводит к сколько-нибудь заметному изменению температуры и давления среды, которые можно, следовательно, считать постоян­ными.

Если бы среды не было, то работа, произведенная телом над теплоизолированным объектом при заданном изменении состояния тела (т. е. заданных начальном и конечном состояниях), была бы вполне определенной величиной, равной изменению энергии тела. Наличие же среды, тоже участвующей в процессе, делает резуль­тат неоднозначным, и возникает вопрос о том, какова максимальная работа, которую может произвести тело при данном изменении его состояния.

Если при переходе из одного состояния в другое тело произ­водит работу над внешним объектом, то при обратном переходе из второго состояния в первое какой-либо внешний источник работы должен производить работу над телом. Прямому переходу, сопровождающемуся совершением телом максимальной работы I R Uax> соответствует обратный переход, осуществление которого требует затраты внешним источником минимальной работы R_min. Очевидно, что работы | R |_тах и R_min совпадают друг с другом, так что задачи об их вычислении полностью эквивалентны, и ниже мы говорим о работе, производимой над телом теплоизолирован­ным внешним источником работы.

В течение процесса тело может обмениваться теплом и работой со средой. Работа, произведенная над телом средой, должна быть, конечно, выделена из полной произведенной над телом работы, так как нас интересует лишь та работа, которая производится данным внешним источником. Таким образом, полное изменение энергии тела АЕ при некотором (не обязательно малом) изменении его состояния складывается из трех частей: из произведенной над телом работы внешнего источника R, из работы, произведен­ной средой, и из полученного от среды тепла. Как уже было указано, благодаря большим размерам среды ее температуру и давление можно считать постоянными; поэтому произведенная ею над телом работа есть PoAV₀, а отданное ею количество тепла

§ 20] ТЕЛО, НАХОДЯЩЕЕСЯ ВО ВНЕШНЕЙ СРЕДЕ 77

равно—T₀AS₀ (буквы с индексом нуль относятся к среде, а без индекса—к телу). Таким образом, имеем:

AE = R+P₀W,—T_ebS_e.

Поскольку объем среды вместе с телом остается неизменным, то ДУ₀ = — ДУ. Далее, в силу закона возрастания энтропии имеем: AS+ASo^O (энтропия теплоизолированного источника работы вообще не меняется), так что AS_U ^—AS. Поэтому из R = AE — — P„AV₀ + ТоAS₀ находим

£>Д£ — T₀AS + P_aAV. (20,1)

Знак равенства достигается при обратимом процессе. Таким образом, мы снова приходим к выводу, что переход совершается с минимальной затратой работы (и, соответственно, обратный переход—с максимальным производством работы), если он про­исходит обратимо. Величина минимальной работы определяется формулой

R_mia = A(E-T₀S + P_aV) (20,2)

(Г₀ и Р₀ как постоянные величины могут быть внесены под знак Д), т. е. эта работа равна изменению величины Е — T₀S + P₀V. Для максимальной работы формула должна быть, очевидно, написана с обратным знаком:

\R\_m^ = -A(E-T₀S + P₀V), (20,3)

так как начальное и конечное состояния меняются местами.

Если в течение процесса тело находится в каждый данный момент в равновесном состоянии (но, конечно, не в равновесии со средой), то для бесконечно малого изменения состояния фор­мулу (20,2) можно написать в другом виде; подставив dE = =*TdS—PdV в dR_min = dE—T₀dS + P₀dV, находим

dR_min = (T-T₀)dS-(P-P₀)dV. (20,4)

Отметим два важных частных случая. Если объем и темпе­ратура тела остаются неизменными, причем последняя равна тем­пературе среды, то из (20,2) имеем: R_mia = A(E—TS), или

#min = ^. (20,5)

т. е. минимальная работа равна изменению свободной энергии тела. Если же постоянны температура и давление тела, причем Т = Т₀, Р = Р₀, то имеем

Ят1п = ЛФ, (20,6)

т. е. работа, произведенная внешним источником, равна измене­нию термодинамического потенциала тела.

Подчеркнем, что в обоих этих частных случаях речь должна идти о теле, которое не находится в равновесии, и поэтому его состояние не определяется одними только Т и V (или Р); в про­тивном случае постоянство этих величин означало бы, что никакого процесса вообще не происходит. Речь может идти, например, о химической реакции в смеси реагирующих друг с другом веществ, о процессе растворения и т. п.

Предположим теперь, что находящееся во внешней среде тело
предоставлено самому себе и над ним не производится никакой
работы. В этом теле будут происходить самопроизвольные необра-
тимые процессы, приводящие его в
л'* _а^ равновесие. В неравенстве (20,1) надо

теперь положить R = 0, поэтому будет

A(£-7₀S + P₀V)<0. (20,7)

Это значит, что в результате про­исходящих с телом процессов вели­чина £ — T₀S + P₀V будет убывать, так что в равновесии она достигнет минимума.

Рис. 3.

В частности, при самопроизволь­ных процессах с постоянными тем-' пературой Т — Т„ и давлением Р = Р₀ убывает термодинамический потенциал тела Ф, а при процессах с постоянными температу­рой Т = Т₀ и объемом тела убывает его свободная энергия F. Эти результаты были уже получены с другой точки зрения в § 15. Отметим, что произведенный здесь вывод по существу не пред­полагает, что температура и объем (или давление) тела остаются постоянными в течение всего процесса: можно утверждать, что термодинамический потенциал (или свободная энергия) тела умень­шится в результате всякого процесса, в начале и конце которого температура и давление (или объем) одинаковы (и равны темпера­туре и давлению среды), даже если они в течение процесса менялись.

Минимальной работе можно приписать еще и другой термо­динамический смысл. Пусть S_n есть полная энтропия тела вместе со средой; если тело находится в равновесии со средой, то S„ есть функция от их полной энергии £„:

S_n = S„(£„).

Пусть тело не находится в равновесии со средой; тогда их сум­марная энтропия отличается от значения S_n(E_n) (при том же значении их суммарной энергии Е_п) на некоторую величину AS„ < 0. На рис. 3 сплошная линия изображает функцию S„ (£_п), а вертикальный отрезок аЬ—величину — А5_П. Горизонтальный же отрезок be есть изменение полной энергии при обратимом переходе тела из состояния равновесия со средой в состояние, соответствующее точке Ъ. Другими словами, этот отрезок изобра­жает минимальную работу, которую должен затратить некоторый внешний источник для приведения тела из состояния равновесия со средой в данное; состояние равновесия, о котором при этом идет речь (точка с на рис. 3), разумеется, не совпадает с состоя­нием равновесия, соответствующим данному значению Е„ (точка а).

Поскольку тело представляет собой весьма малую часть всей системы, то происходящие с ним процессы приводят лишь к отно­сительно ничтожным изменениям полных энергии и энтропии. Из графика на рис. 3 следует поэтому, что

АО______ р

^п~" dE„ ^Amin-

Но производная dE„/dS„ есть равновесная температура системы, т. е. температура среды Т₀. Таким образом,

AS_n = -^ = -^(A£-7₀AS + />„AV). (20,8)

Эта формула определяет, насколько отличается энтропия замкну­той системы (тело + среда) от своего наибольшего возможного зна­чения, если тело не находится в равновесии со средой; при этом АЕ, AS и AV—разности между энергией, энтропией и объемом тела и их значениями в состоянии полного равновесия.

§ 21. Термодинамические неравенства

Получая условия теплового равновесия из условия максималь­ности энтропии, мы до сих пор рассматривали лишь ее первые производные. Требуя обращения в нуль производных по энергии и объему, мы получили (§§ 9, 12) в качестве условий равновесия условия равенства температур и давлений во всех частях тела. Однако равенство нулю первых производных является лишь не­обходимым условием экстремума и не обеспечивает того, чтобы энтропия имела именно максимум. Выяснение же достаточных условий максимума требует, как известно, исследования второго дифференциала функции.

¹) Что касается зависимости энтропии от импульсов макроскопического дви­жения, то для нее нами уже были исследованы условия, налагаемые как на первые, так и на вторые производные (§ 10), в результате чего были найдены требование отсутствия внутренних макроскопических движений в'теле и требо­вание положительности температуры.

Это исследование, однако, удобнее произвести, исходя не непо­средственно из условия максимальности энтропии замкнутой си­стемы, а из другого, эквивалентного ему условия¹). Выделим из рассматриваемого тела некоторую малую (но макроскопическую) часть. По отношению к этой части остальные области тела можно рассматривать как внешнюю среду. Тогда, как мы видели в пре­дыдущем параграфе, можно утверждать, что в равновесии имеет минимум величина

E-T₀S + P₀V,

где Е, S, V—энергия, энтропия и объем данной части тела, а Т₉, Р_а—температура и давление среды, т. е. остальных частей тела. Т₀ и Р₀ являются, очевидно, в то же время температурой и давлением рассматриваемой части в состоянии равновесия.

Таким образом, при всяком малом отклонении от равновесия изменение величины Е—T₀S + P₀V должно быть положительно, т. е.

6E — T_obS + P₀8V>0. (21,1)

Другими словами, можно сказать, что минимальная работа, кото­рую надо затратить для того, чтобы перевести данную часть тела из состояния равновесия в любое другое близкое состояние, должна быть положительна.

В дальнейшем во всех коэффициентах, стоящих при отклоне­ниях термодинамических величин от их равновесных значений, будут подразумеваться равновесные значения, соответственно чему индексы нуль будут опускаться.

Разлагая 8Е в ряд (рассматривая Е как функцию S и V"), получим с точностью до членов второго порядка

Но дЕ/dS — T, dE/dV = — Р, так что члены первого порядка здесь равны T8S—P8V и при подстановке 8Е в (21,1) сокращаются. Таким образом, получаем условие

Ш^6S2+² шът^{6S бУ} + -Щ-^ьу2 > °- <²¹ -²)

Как известно, для того чтобы такое неравенство имело место при произвольных 65 и 8V, необходимо соблюдение двух условий¹):

g->0, (21,3)

dS² dV*

Поскольку

dS* ~\dS)v~ C_v

то условие (21,3) приобретает вид TIC_V~>Q или

C_v>0, (21,5)

т. е. теплоемкость при постоянном объеме всегда положительна.

^х) Особый случай, когда в (21,4) стоит знак равенства, будет рассмотрен в дальнейшем, в § 152.

§ 21]

термодинамические неравенства

Условие (21,4) можно написать в виде якобиана

^d[{ds)_v' {dv)_s] _________ д_

d(S,V) ~ d(S,V)

Переходя к переменным Т и V, имеем

д(Т, Р) [дР\

д (Г, Р) _ д(Т,У) _ V дУ)_т _ Т (дР \

d(S,V) - д(S,V) - (_dS_\ ~ C_v { dV)_т

д(Т,У) \дТ)у

Поскольку C_v > 0, это равносильно условию

(ж)_г<°.

(21,6)

т. е. увеличение объема при постоянной температуре всегда со­провождается уменьшением давления.

Условия (21,5) и (21,6) называются термодинамическими не­равенствами. Состояния, в которых эти условия не выполнены, неустойчивы и в природе существовать не могут.

В § 16 было уже отмечено, что в силу неравенства (21,6) и формулы (16,10) всегда C_p>C_v. Ввиду (21,5) можно поэтому заключить, что всегда и

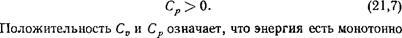
возрастающая функция температуры при постоянном объеме, а теп­ловая функция—такая же функция температуры, но при постоян­ном давлении. Энтропия же монотонно возрастает с температурой как при постоянном объеме, так и при постоянном давлении.

Условия (21,5—6), выведенные для любой малой части тела, справедливы, конечно, и для всего тела в целом, так как в рав­новесии температуры и давления всех частей равны друг другу. При этом предполагается, что тело однородно (только такие тела мы пока и рассматриваем). Подчеркнем, что выполнение условий (21,5 — 6) связано именно с однородностью тела. Можно, напри­мер, рассмотреть тело, частицы которого удерживаются вместе гравитационными силами; такое тело будет, очевидно, неодно­родным,— оно будет уплотнено по направлению к центру. Для такого тела в целом теплоемкость может быть и меньше нуля, т. е. тело может нагреваться по мере уменьшения энергии. Заме­тим, что это не противоречит тому, что теплоемкость положи­тельна для каждой малой части тела, так как энергия всего тела в таких условиях не равна сумме энергий его частей—суще­ствует еще дополнительная энергия гравитационного взаимодей­ствия между этими частями.

Дата добавления: 2014-11-07