
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение точки по окружности
|
|
|
|
Уравнения равномерного и равноускоренного движений
В случае равномерного прямолинейного движения материальной точки ( ) функция
) функция 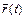 имеет вид:
имеет вид:
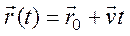 ,
,
а для равнопеременного движения ( ):
):
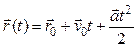 .
.
Здесь 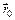 – начальное положение точки,
– начальное положение точки,  ;
; 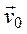 – начальная скорость.
– начальная скорость.
При решении задач часто удобно записывать функцию 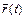 непосредственно в проекциях на оси координат. Тогда при постоянном ускорении
непосредственно в проекциях на оси координат. Тогда при постоянном ускорении 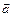 функцию
функцию 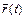 можно представить в виде двух уравнений:
можно представить в виде двух уравнений:
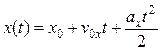 ,
, 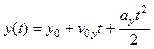 .
.
В частности, при движении материальной точки под действием силы тяжести удобно выбрать ось  вертикально вверх. В этом случае вектор ускорения имеет лишь одну проекцию, отличную от нуля (
вертикально вверх. В этом случае вектор ускорения имеет лишь одну проекцию, отличную от нуля ( ,
, 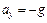 , где
, где 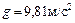 ):
):
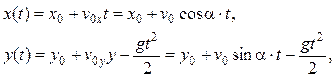
где 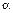 – угол, образованный вектором начальной скорости
– угол, образованный вектором начальной скорости  с горизонтом. Часто удобно поместить начало координат в начальной точке траектории (
с горизонтом. Часто удобно поместить начало координат в начальной точке траектории (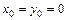 ).
).
Средняя угловая скорость за время 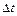 равна отношению угла поворота радиус-вектора точки за время
равна отношению угла поворота радиус-вектора точки за время 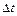 к этому времени
к этому времени 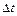 :
:
 .
.
Мгновенная угловая скорость равна первой производной угла поворота по времени:
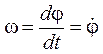 .
.
Среднее угловое ускорение за время 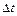 равно отношению приращения угловой скорости за время
равно отношению приращения угловой скорости за время 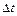 к этому времени:
к этому времени:
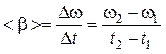 .
.
Мгновенное угловое ускорение равно первой производной угловой скорости или второй производной угла поворота по времени:
 .
.
Связь между линейной и угловой скоростями материальной точки:
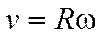 ,
,
где 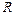 – радиус окружности.
– радиус окружности.
Связь между линейным и угловым ускорениями материальной точки:
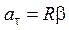 .
.
Бесконечно малое угловое перемещение 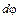 материальной точки является вектором. Поэтому угловая скорость является векторной величиной:
материальной точки является вектором. Поэтому угловая скорость является векторной величиной:
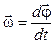 ,
,
а направление вектора 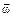 определяется по правилу правого винта.
определяется по правилу правого винта.
Вектор линейной скорости материальной точки выражается через вектор угловой скорости через векторное произведение:
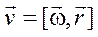 .
.
Угловое ускорение также является векторной величиной:
 .
.
При движении точки по окружности вектор 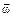 меняется лишь по модулю, а по направлению совпадает с неизменной осью вращения.
меняется лишь по модулю, а по направлению совпадает с неизменной осью вращения.
Задача 1.1. Радиус-вектор точки изменяется со временем по закону 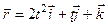 (м). Найти скорость
(м). Найти скорость 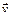 и ускорение
и ускорение  точки, модуль скорости
точки, модуль скорости 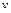 в момент
в момент 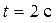 , а также приближенное значение пути
, а также приближенное значение пути 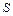 , пройденного точкой за 10-ю секунду движения, и среднюю скорость прохождения этого пути
, пройденного точкой за 10-ю секунду движения, и среднюю скорость прохождения этого пути 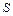 .
.
Дано: Решение:
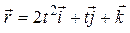 (м) (м)
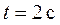
| Вектор скорости 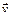 есть первая производная радиус-вектора по времени: есть первая производная радиус-вектора по времени:
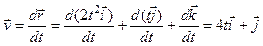 . .
|
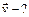
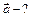
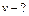
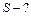

| Отсюда видно, что вектор скорости имеет только две компоненты:  и и 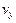 .
Вектор ускорения .
Вектор ускорения  есть первая производная от вектора скорости по времени: есть первая производная от вектора скорости по времени:
 . .
|
Получается, что вектор ускорения имеет только одну компоненту, не зависящую от времени 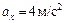 , значит, движение вдоль оси
, значит, движение вдоль оси 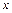 является равноускоренным, а вдоль оси
является равноускоренным, а вдоль оси 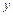 – равномерным.
– равномерным.
Найдем теперь модуль скорости. Так как 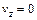 , то
, то
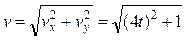
и в момент времени 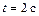
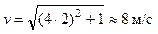 .
.
Для нахождения пути 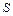 , пройденного точкой за 10-ю секунду движения, можно считать его приближенно равным перемещению, так как промежуток времени достаточно мал. Тогда найдем перемещение
, пройденного точкой за 10-ю секунду движения, можно считать его приближенно равным перемещению, так как промежуток времени достаточно мал. Тогда найдем перемещение  за время
за время 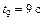 и
и 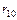 за время
за время 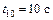 и возьмем их разность. Учитывая
и возьмем их разность. Учитывая
 ,
,
получим
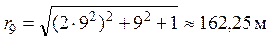 ,
, 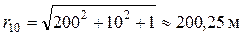 ,
,
тогда путь за 10-ю секунду движения
 .
.
Среднюю скорость прохождения пути 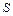 нетрудно найти:
нетрудно найти:
 .
.
Следует заметить, что в строгом смысле для нахождения пути 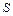 надо сначала установить зависимость длины пути от времени. Тогда можем найти точно путь за 9 и за 10 секунд. Функция
надо сначала установить зависимость длины пути от времени. Тогда можем найти точно путь за 9 и за 10 секунд. Функция  нам известна, тогда:
нам известна, тогда:
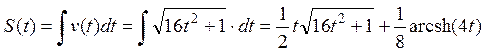 .
.
Откуда найдем требуемый путь:
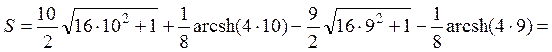
 .
.
Получаем такой же результат.
Ответ: 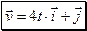 ,
, 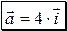 ,
,
 ,
, 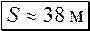 ,
, 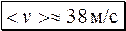 .
.
Задача 1.2. Тело падает с высоты  без начальной скорости. Какой путь пройдет тело за
без начальной скорости. Какой путь пройдет тело за 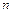 -ую секунду своего падения, за последнюю секунду? За какое время тело пройдет
-ую секунду своего падения, за последнюю секунду? За какое время тело пройдет 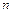 -ый метр своего пути, последний метр?
-ый метр своего пути, последний метр?
Дано: Решение:


| На примере этой задачи продемонстрируем, как удачно выбранная система координат может значительно упростить | 
|

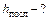
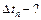

| решение. Выберем систему координат, начало которой совпадает с начальным положением тела, а ось координат направлена вертикально вниз (см. рис.). В этой системе координат уравнение движения имеет вид: | |
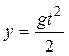 .
.
В момент времени 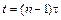 тело находится в точке
тело находится в точке 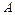 , а в момент времени
, а в момент времени 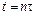 – в точке
– в точке 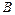 , где
, где 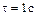 ,
, 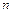 – число секунд падения до точки
– число секунд падения до точки 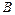 . Координаты точек
. Координаты точек 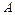 и
и 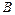 соответственно равны:
соответственно равны:
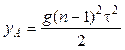 ,
, 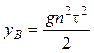 .
.
Решая совместно два последних уравнения с учетом того, что  , имеем:
, имеем:
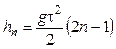 .
.
В момент времени, когда тело достигло Земли, 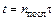 ,
, 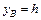 :
:
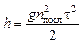 .
.
Тогда путь, пройденный телом за последнюю секунду:
 .
.
Для нахождения времени 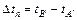 прохождения
прохождения 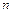 -го метра своего пути, введем координаты начала и конца этого метра:
-го метра своего пути, введем координаты начала и конца этого метра: 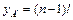 ,
, 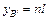 , где
, где 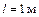 . Тогда можно написать:
. Тогда можно написать:
 ,
, 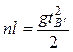 .
.
Решая совместно два последних уравнения:
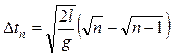 .
.
Когда тело достигло Земли 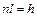 , тогда время прохождения последнего метра:
, тогда время прохождения последнего метра:
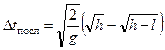 .
.
Можно выбрать другую систему координат, связанную с Землей: начало координат в точке падения, ось координат направлена вертикально вверх. Тогда уравнение движения примет вид:
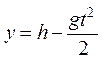 .
.
Используя другие начальные (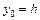 ) и конечные (
) и конечные ( ) условия, получим те же самые ответы.
) условия, получим те же самые ответы.
Можно выбрать систему координат и другим способом: с началом в точке бросания тела и осью, направленной вверх. Несложно проверить, что решение соответствующих уравнений приведут к тем же результатам.
Ответ: 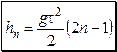 ,
, 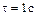 ;
; 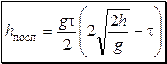 ,
,
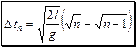 ,
, 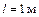 ;
; 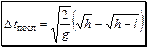 .
.
Задача 1.3. Снаряд вылетает со скоростью  из ствола орудия, стоящего у подножия горы, поверхность которой наклонена под углом
из ствола орудия, стоящего у подножия горы, поверхность которой наклонена под углом 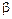 к горизонту. Каким должен быть угол
к горизонту. Каким должен быть угол  стрельбы по отношению к горизонту, чтобы имело место максимальная дальность полета снаряда. Найти также расстояние
стрельбы по отношению к горизонту, чтобы имело место максимальная дальность полета снаряда. Найти также расстояние 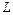 вдоль горизонта, куда попал снаряд при таком выстреле.
вдоль горизонта, куда попал снаряд при таком выстреле.
Дано: Решение:
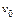
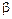
| Выберем систему координат, начало которой находится у подножия горы (см. рис.). | 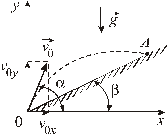
|
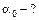

| Запишем уравнения движения снаряда вдоль координатных осей:
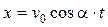 , ,
 . .
| |
Заметим, что система уравнений 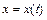 ,
, 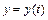 являются уравнениями движения снаряда в параметрическом виде.
являются уравнениями движения снаряда в параметрическом виде.
Исключая неизвестное время  , приведем уравнение движения к виду:
, приведем уравнение движения к виду:
 .
.
Уравнение такого вида 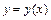 является уравнением движения в каноническом виде.
является уравнением движения в каноническом виде.
Для прямой  , где
, где 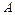 – точка приземления снаряда, можно записать уравнение
– точка приземления снаряда, можно записать уравнение 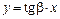 . Приравнивая правые части двух последних уравнений, получим:
. Приравнивая правые части двух последних уравнений, получим:
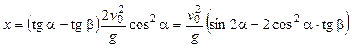 .
.
Наибольшую дальность полета снаряда найдем из условия
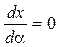 ,
,
откуда находим:
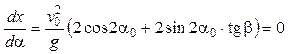 .
.
С учетом того, что 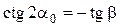 и, следовательно,
и, следовательно, 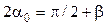 , имеем:
, имеем:
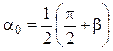 .
.
Таким образом, наибольшая дальность полета снаряда будет иметь место при угле бросания, равном сумме  и половине угла откоса
и половине угла откоса  .
.
Подставляя в выражение для 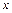 значение угла
значение угла  , получим максимальное расстояние, куда может попасть снаряд:
, получим максимальное расстояние, куда может попасть снаряд:
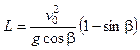 .
.
Ответ: 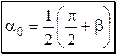 ,
,  .
.
Задача 1.4. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота  по закону
по закону 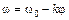 , где
, где 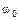 и
и 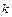 – положительные постоянные. В момент времени
– положительные постоянные. В момент времени 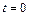 угол
угол 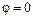 . Найти зависимости от времени: а) угла поворота; б) угловой скорости.
. Найти зависимости от времени: а) угла поворота; б) угловой скорости.
Дано: Решение:
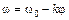
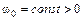
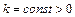
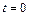 , , 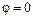
| Используя определение угловой скорости:
 ,
получим линейное дифференциальное уравнение первого порядка относительно угла поворота ,
получим линейное дифференциальное уравнение первого порядка относительно угла поворота 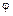 : :
|
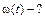
|  .
Разделяя переменные, получим: .
Разделяя переменные, получим:
|
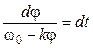 .
.
Интегрируем обе части полученного выражения с учетом начальных условий задачи. Угол поворота меняется от 0 до 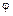 , а время от 0 до
, а время от 0 до  :
:
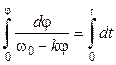 .
.
После интегрирования имеем:
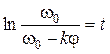 ,
,
откуда получаем искомую зависимость угла поворота от времени:
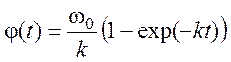 .
.
Взяв от полученного выражения первую производную по времени, получим зависимость угловой скорости от времени:
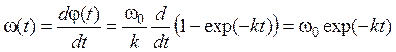 .
.
Графический вид найденных функций  и и  представлен на рисунке.
Ответ: представлен на рисунке.
Ответ:
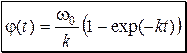 , ,
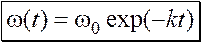 . .
|
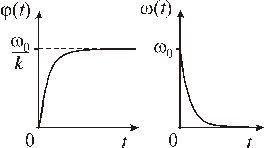
|
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 1288; Нарушение авторских прав?; Мы поможем в написании вашей работы!