
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Волны. Звуковые волны
|
|
|
|
Волнами называются возмущения, распространяющиеся в среде (или в вакууме) и несущие с собой энергию.
Различают волны продольные и поперечные. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной – в направлениях, перпендикулярных к направлению распространения волны.
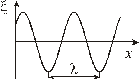 Расстояние
Расстояние 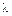 , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Связь длины волны с периодом колебаний
, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Связь длины волны с периодом колебаний
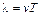 ,
,
где 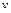 – скорость распространения волны, которая является фазовой скоростью.
– скорость распространения волны, которая является фазовой скоростью.
Уравнение плоской незатухающей волны
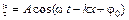 ,
,
где 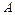 – амплитуда колеблющихся точек,
– амплитуда колеблющихся точек, 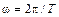 – циклическая частота,
– циклическая частота, 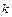 – волновое число, равное
– волновое число, равное
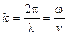 .
.
Для волны, распространяющейся в произвольном направлении, уравнение будет иметь вид
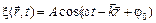 ,
,
где 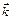 – волновой вектор, равный по модулю волновому числу и имеющий направление нормали к волновой поверхности.
– волновой вектор, равный по модулю волновому числу и имеющий направление нормали к волновой поверхности.
Фазовая скорость продольных волн равна
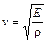 ,
,
где 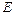 – модуль Юнга,
– модуль Юнга, 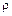 – плотность среды.
– плотность среды.
Фазовая скорость поперечных волн
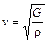 ,
,
где 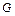 – модуль сдвига.
– модуль сдвига.
Средняя плотность энергии, то есть энергия волны, приходящая на единицу объема и усредненная по периоду, определяется выражением
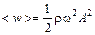 .
.
Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность
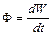 .
.
Плотность потока энергии численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия,
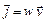 .
.
Плотность потока энергии является векторной величиной с направлением, совпадающим с направлением распространения волны и переноса энергии.
Среднее по времени значение плотности потока энергии, переносимой волной, называется интенсивностью волны.
При интерференции волн максимум и минимум амплитуды получается соответственно при условиях
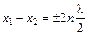 (
(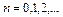 ),
),
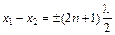 (
(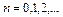 ).
).
Звуковыми волнами или звуком называются волны, распространяющиеся в упругой среде и имеющие частоту в пределах от 20 до 20000 Гц.
Уровень громкости 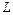 определяется как логарифм отношения интенсивности данного звука
определяется как логарифм отношения интенсивности данного звука 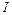 к интенсивности
к интенсивности 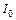 , принятой за исходную. Значение
, принятой за исходную. Значение 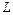 в децибелах (дБ) определяется формулой
в децибелах (дБ) определяется формулой
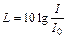 ,
,
где 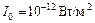 .
.
По принципу Доплера частота звука, воспринимаемая наблюдателем, определяется формулой
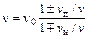 ,
,
где 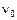 – частота излучаемых колебаний,
– частота излучаемых колебаний, 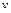 – скорость распространения звука,
– скорость распространения звука, 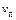 – скорость движения приемника (наблюдателя),
– скорость движения приемника (наблюдателя), 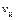 – скорость движения источника. Перед скоростью
– скорость движения источника. Перед скоростью 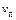 знак «+», если приемник приближается к источнику; «–», если приемник удаляется от источника. Перед скоростью
знак «+», если приемник приближается к источнику; «–», если приемник удаляется от источника. Перед скоростью 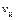 знак «–», если источник приближается к приемнику; «+», если источник удаляется от приемника.
знак «–», если источник приближается к приемнику; «+», если источник удаляется от приемника.
Задача 6.1. Волна с частотой 4 Гц распространяется в пространстве со скоростью 6 м/с. Найти в градусах разность фаз волны в двух точках пространства, отстоящих друг от друга на расстоянии 50 см и расположенных на прямой, совпадающей с направлением распространения волны.
Дано: Решение:
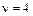 Гц Гц
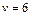 м/с м/с
 см см
| Две точки волны, отстоящих друг от друга на расстоянии 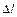 , отличаются по фазе на , отличаются по фазе на
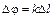 , (1) , (1)
|
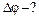
| где 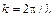 – волновое число. – волновое число.
|
Длину волны 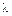 находим из
находим из
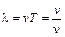 . (2)
. (2)
Подставляя (2) в (1) с учетом выражения для 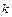 , получим:
, получим:
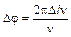 ;
; 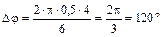 .
.
Ответ:
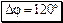 .
.
Задача 6.2. Амплитуда звуковой волны увеличилась в 10 раз. На сколько увеличился уровень громкости?
Дано: Решение:
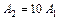
| Используя выражение для уровня громкости
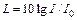 , ,
|
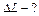
| можно записать |
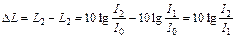 .
.
Так как интенсивность волны пропорциональна квадрату амплитуды 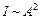 , окончательно получим
, окончательно получим
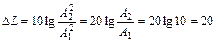 дБ.
дБ.
Ответ:
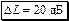 .
.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 525; Нарушение авторских прав?; Мы поможем в написании вашей работы!