
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинематика и динамика гармонических колебаний
|
|
|
|
Колебаниями называется такое движение, при котором система при своем движении многократно проходит через определенное положение, например, положение равновесия. Если повторения происходят через одинаковое время, то колебания являются периодическими, а интервал времени, в течение которого происходит повторение, называется периодом.
Свободными или собственными колебаниями называются такие колебания, которые совершает система, выведенная из положения равновесия, и предоставленная самой себе.
Простейший вид колебаний – гармонические, то есть такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса:
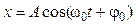 ,
,
где 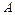 – амплитуда (наибольшее отклонение системы от положения равновесия),
– амплитуда (наибольшее отклонение системы от положения равновесия), 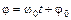 – фаза колебаний (показывает состояние колеблющейся системы в данный момент времени),
– фаза колебаний (показывает состояние колеблющейся системы в данный момент времени), 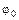 – начальная фаза колебаний,
– начальная фаза колебаний, 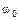 – круговая или циклическая частота собственных колебаний.
– круговая или циклическая частота собственных колебаний.
Скорость и ускорение точки, совершающей колебания, определяются соотношением:
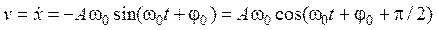 ,
,
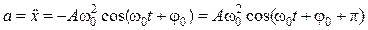 .
.
Потенциальная и кинетическая энергии колеблющейся точки:
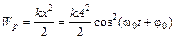 ,
,
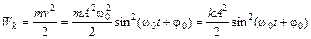 .
.
Кинетическая и потенциальная энергии в отдельности не остаются постоянными, а совершают гармонические колебания вокруг общего среднего значения 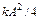 с удвоенной круговой частотой
с удвоенной круговой частотой 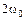 .
.
Полная энергия точки, колеблющейся без затухания, остается величиной постоянной:
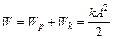 .
.
Период пружинного маятника (тело массой 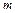 , прикрепленное к пружине жесткостью
, прикрепленное к пружине жесткостью 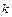 ) равен:
) равен:
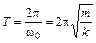 .
.
Период математического маятника (идеализированная система, состоящая из невесомой и нерастяжимой нити длиной 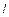 , на которую подвешена масса, сосредоточенная в одной точке) равен:
, на которую подвешена масса, сосредоточенная в одной точке) равен:
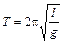 ,
,
где 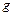 – ускорение свободного падения.
– ускорение свободного падения.
Период физического маятника (твердое тело произвольной формы, которое может колебаться вокруг точки подвеса, находящейся выше центра масс) равен:
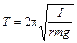 ,
,
где 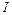 – момент инерции маятника относительно его оси вращения,
– момент инерции маятника относительно его оси вращения, 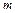 – масса маятника,
– масса маятника, 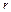 – расстояние от оси вращения до центра масс.
– расстояние от оси вращения до центра масс.
Задача 5.1. Материальная точка массой 10 г колеблется по закону 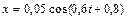 (м). Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.
(м). Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.
Дано: Решение:
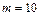 г г
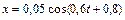
| Сравнивая уравнение, данное в задаче
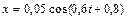 , ,
|
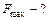
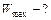
| с уравнением гармонических колебаний в общем виде
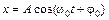 ,
находим: ,
находим:
|
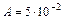 м,
м, 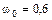 рад/с,
рад/с, 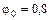 рад.
рад.
Модуль силы, вызывающей гармонические колебания, равен
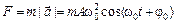 ,
,
откуда получаем
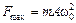 ;
; 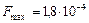 Н
Н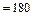 мкН.
мкН.
Полная энергия колеблющейся точки
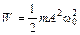 ;
; 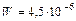 Дж
Дж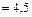 мкДж.
мкДж.
Ответ:
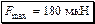 ,
, 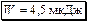 .
.
Задача 5.2. Период колебаний математического маятника на уровне Земли равен 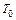 . Насколько изменится период колебаний маятника, если его поднять на высоту
. Насколько изменится период колебаний маятника, если его поднять на высоту 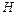 над поверхностью Земли? Землю считать шаром радиуса
над поверхностью Земли? Землю считать шаром радиуса 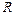 .
.
Дано: Решение:
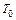
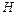
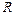
| Период колебаний математического маятника на поверхности Земли будет равен:
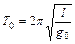 , ,
|
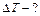
| где 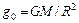 ( (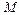 – масса Земли, – масса Земли, 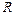 – радиус Земли), а на высоте – радиус Земли), а на высоте 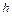 над поверхностью Земли период будет над поверхностью Земли период будет
|
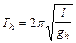 ,
,
где 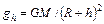 .
.
Относительное изменение периода колебаний маятника составит величину:
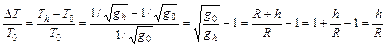 ,
,
откуда получаем ответ:
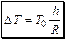 .
.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 3186; Нарушение авторских прав?; Мы поможем в написании вашей работы!