
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение состояния газа
|
|
|
|
Кубический сантиметр воздуха при P = 1 атм и Т = 20о С содержит примерно 3.0 * 1019 молекул. Для точного описания их движения понадобилось бы порядка 1020 уравнений механики.
Статистическая физика рассматривает усредненные параметры: давление, температуру и плотность газа.
Уравнение состояния газа определяет связь его температуры  , давления
, давления 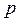 и объема
и объема  в состоянии термодинамического равновесия.
в состоянии термодинамического равновесия.
Идеальным называется газ, размерами молекул которого можно пренебречь по сравнению с его объемом, и в котором силы взаимодействия между молекулами пренебрежимо малы.
Для идеального газа уравнение состояния имеет следующий вид
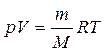 ,
,
где 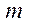 – масса газа,
– масса газа, 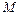 – молярная масса вещества,
– молярная масса вещества, 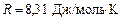 – универсальная газовая постоянная.
– универсальная газовая постоянная.
Величина 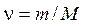 выражает количество вещества в молях.
выражает количество вещества в молях.
В одном моле любого вещества содержится одинаковое число частиц, равное 6,02·1023.
Число частиц, содержащихся в моле вещества, называется числом или постоянной Авогадро 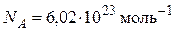 .
.
Закон Авогадро: один моль любого газа при одинаковых температуре и давлении занимает один и тот же объем. При нормальных условиях этот молярный объем равен 22,4 л.
Нормальные физические условия определяются давлением 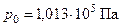 (нормальная атмосфера), температурой
(нормальная атмосфера), температурой 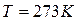 .
.
Частными случаями уравнения Клапейрона–Менделеева (при 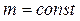 ) являются опытные газовые законы:
) являются опытные газовые законы:
при 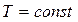 (изотермический процесс); Закон Бойля–Мариотта
(изотермический процесс); Закон Бойля–Мариотта
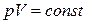 или
или 
при 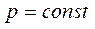 (изобарический процесс) Закон Гей–Люссака:
(изобарический процесс) Закон Гей–Люссака:
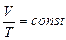 или
или 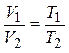
при 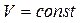 (изохорический процесс) Закон Шарля:
(изохорический процесс) Закон Шарля:
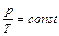 или
или 
Закон Дальтона: давление смеси газов равно сумме их парциальных давлений, то есть давлений, которые имел бы каждый из этих газов в отдельности, если бы он при данной температуре один занимал весь объем.
Уравнение Менделеева-Клапейрона можно сформулировать в виде:
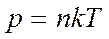
где 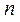 – число молекул в единице объема (концентрация молекул), а
– число молекул в единице объема (концентрация молекул), а 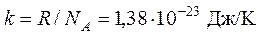 – постоянная Больцмана.
– постоянная Больцмана.
Учитывая, что средняя кинетическая энергия поступательного движения молекулы:
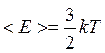 .
. 
получим основное уравнение молекулярно-кинетической теории газов
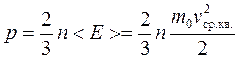 ,
,
где 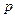 – давление,
– давление, 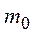 – масса одной молекулы,
– масса одной молекулы,  – средняя квадратичная скорость молекулы.
– средняя квадратичная скорость молекулы.
наиболее вероятная скорость молекул: 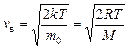
средняя квадратичная скорость,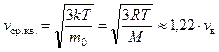
средняя скорость.
Задача 7.1. В цилиндре под поршнем находится воздух при давлении  Па и температуре
Па и температуре 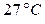 . С какой силой надо действовать на поршень после нагревания воздуха до температуры
. С какой силой надо действовать на поршень после нагревания воздуха до температуры 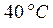 , чтобы объем воздуха в цилиндре был равен первоначальному? Площадь поршня
, чтобы объем воздуха в цилиндре был равен первоначальному? Площадь поршня  .
.
Дано: Решение:
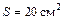
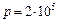 Па Па
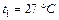
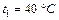
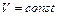
| Так как объем воздуха в цилиндре остается постоянным, можно применить закон Шарля:
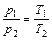 . (1)
Для того чтобы поршень был в равновесии и объем воздуха не изменялся, необходимо, чтобы сила, с которой . (1)
Для того чтобы поршень был в равновесии и объем воздуха не изменялся, необходимо, чтобы сила, с которой
|
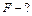
| действуют на поршень, была равна увеличению силы давления воздуха при нагревании |
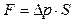 . (2)
. (2)
Давление воздуха внутри цилиндра возросло на
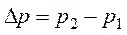 . (3)
. (3)
Подставляя в (3) значение 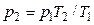 , найденное из (1), получим
, найденное из (1), получим
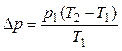 .
.
Подставляя полученное выражение в (2), получим ответ:
 Н.
Н.
Ответ: 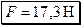 .
.
Задача 7.2. Определить плотность кислорода при давлении 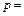
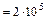 Па, если средняя квадратичная скорость молекул
Па, если средняя квадратичная скорость молекул  м/с.
м/с.
Дано: Решение:
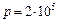 Па Па
 м/с м/с
| Задачу можно решить двумя способами. В 1-ом способе используется уравнение состояния Кла пейрона–Менделеева:
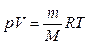 , ,
|
откуда плотность газа
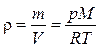 .
.
С учетом того, что 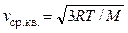 , сразу имеем ответ:
, сразу имеем ответ:
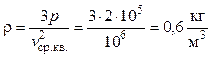 .
.
2 способ предполагает использование основного уравнения молекулярно-кинетической теории в виде:
 ,
,
где 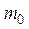 – масса одной молекулы,
– масса одной молекулы, 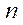 – концентрация молекул.
– концентрация молекул.
Поскольку по определению плотность газа равна  , получим тот же ответ:
, получим тот же ответ:
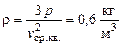 .
.
Ответ:
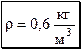 .
.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 1803; Нарушение авторских прав?; Мы поможем в написании вашей работы!