
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика вращательного движения твердого тела
|
|
|
|
Абсолютно твердое тело – это такая идеализированная система, в которой расстояния между любыми точками остаются неизменными при любых движениях системы.
Движение твердого тела в общем случае можно представить в виде суммы поступательного и вращательного движения.
Поступательное это такое движение, при котором любая линия, проведенная в теле, при движении остается параллельной самой себе. При поступательном движении динамика твердого тела сводится к динамике одной точки, в качестве которой берут центр масс.
Центром масс системы называется точка 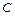 , положение которой задается радиус-вектором
, положение которой задается радиус-вектором 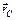 , определяемым следующим образом:
, определяемым следующим образом:
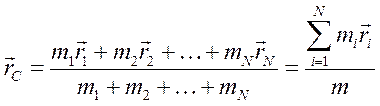 .
.
Вращательное это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Моментом силы 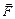 относительно точки
относительно точки 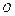 называется векторное произведение радиус-вектора силы относительно точки
называется векторное произведение радиус-вектора силы относительно точки 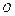 на вектор силы
на вектор силы
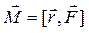 .
.
Моментом 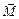 нескольких сил относительно точки называется сумма моментов этих сил относительно той же точки:
нескольких сил относительно точки называется сумма моментов этих сил относительно той же точки:
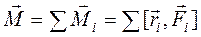 .
.
Моментом импульса 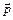 материальной точки относительно точки
материальной точки относительно точки 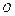 называется векторное произведение
называется векторное произведение
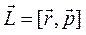 .
.
Для системы материальных точек моментом импульса относительно некоторого начала 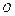 называется сумма моментов этих точек относительно того же начала.
называется сумма моментов этих точек относительно того же начала.
Момент силы и момент импульса относительно точки есть вектор. Момент силы и момент импульса относительно оси есть проекция на эту ось момента относительно точки, лежащей на той же оси, то есть является скалярной величиной.
Уравнение моментов (или закон изменения момента импульса):
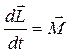 ,
,
то есть производная по времени от момента импульса материальной точки (системы материальных точек) относительно произвольного неподвижного начала равна геометрической сумме моментов всех внешних сил относительно того же начала 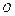 .
.
Если момент внешних сил относительно неподвижного начала 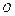 равен нулю, то момент импульса системы относительно того же начала остается постоянным во времени. Это утверждение называется законом сохранения момента импульса. В частности, это имеет место для изолированной системы материальных точек. Если имеет место случай центральных сил, когда направления всех сил, действующих на материальные точки системы, проходят через неподвижный центр
равен нулю, то момент импульса системы относительно того же начала остается постоянным во времени. Это утверждение называется законом сохранения момента импульса. В частности, это имеет место для изолированной системы материальных точек. Если имеет место случай центральных сил, когда направления всех сил, действующих на материальные точки системы, проходят через неподвижный центр 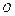 , то момент импульса системы относительно точки
, то момент импульса системы относительно точки 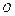 также остается постоянным во времени.
также остается постоянным во времени.
Моментом инерции системы материальных точек относительно некоторой оси называется величина, равная сумме произведений масс материальных точек на квадраты расстояний их до оси вращения:
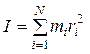 .
.
Основное уравнение динамики вращательного движения:
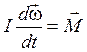 ,
,
то есть произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.
Момент импульса материальной точки при вращательном движении можно определить также как произведение момента инерции точки на угловую скорость:
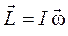 .
.
Если вещество в теле распределено непрерывно, то его момент инерции определяется в виде интеграла
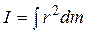 ,
,
где 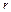 – расстояние от элемента массы
– расстояние от элемента массы 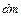 до оси вращения.
до оси вращения.
Момент инерции тела характеризует меру инертности при вращательном движении.
Частные случаи момента инерции:
– момент инерции бесконечно тонкого круглого кольца (окружности) радиуса 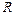 относительно оси, проходящей через центр симметрии и перпендикулярной плоскости кольца:
относительно оси, проходящей через центр симметрии и перпендикулярной плоскости кольца:
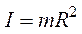 ;
;
– момент инерции полого однородного цилиндра радиуса 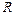 с бесконечно тонкими стенками относительно его геометрической оси:
с бесконечно тонкими стенками относительно его геометрической оси:
 ;
;
– момент инерции однородного сплошного диска радиуса 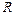 относительно оси, проходящей через центр диска и перпендикулярной к его плоскости:
относительно оси, проходящей через центр диска и перпендикулярной к его плоскости:
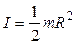 ;
;
– момент инерции однородного сплошного цилиндра радиуса 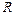 относительно его продольной геометрической оси:
относительно его продольной геометрической оси:
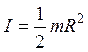 ;
;
– момент инерции тонкого однородного стержня длины 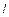 относительно перпендикулярной оси, проходящей через центр масс:
относительно перпендикулярной оси, проходящей через центр масс:
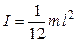 ;
;
– момент инерции сплошного однородного шара радиуса 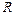 :
:
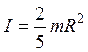 .
.
Теорема Гюйгенса–Штейнера:
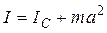 ,
,
то есть момент инерции тела относительно любой оси равен моменту инерции этого тела относительно оси, проходящей через центр масс параллельно заданной, сложенному с произведением массы тела на квадрат расстояния между осями.
Если материальная точка вращается по окружности, то элементарная работа при повороте на угол 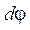 равна
равна
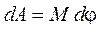 .
.
Кинетическая энергия вращающегося твердого тела определяется как
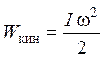 .
.
Задача 4.1. Найти момент инерции тонкого однородного стержня длины 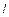 и массы
и массы 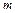 : а) относительно перпендикулярной к стержню оси, проходящей через центр масс; б) относительно перпендикулярной к стержню оси, проходящей через конец стержня.
: а) относительно перпендикулярной к стержню оси, проходящей через центр масс; б) относительно перпендикулярной к стержню оси, проходящей через конец стержня.
Дано: Решение:
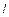
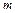
| Предполагается, что стержень однородный, то есть вещество распределено в нем с постоянной плотностью, и бесконечно тонкий, то есть поперечные размеры стержня очень малы по сравнению с его длиной. |
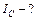
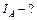
| Рассмотрим сначала случай, когда ось проходит через центр стержня 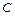 , который является центром масс. Выделим бесконечно малый элемент стержня массой , который является центром масс. Выделим бесконечно малый элемент стержня массой 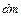 , находящийся на расстоянии , находящийся на расстоянии 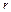 от оси вращения и имеющий длину от оси вращения и имеющий длину 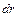 (см. рис.). Объем такого элемента равен (см. рис.). Объем такого элемента равен 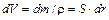 , где , где 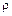 – плотность стержня, – плотность стержня, 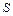 – площадь его поперечного сечения. С учетом – площадь его поперечного сечения. С учетом 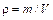 , где , где 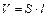 – объем всего стержня, получим – объем всего стержня, получим
|
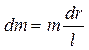 .
.
Момент инерции этого элемента найдется по формуле 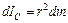 , а момент инерции всего стержня определяется интегралом
, а момент инерции всего стержня определяется интегралом
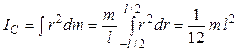 . (1)
. (1)
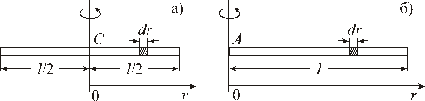
Пусть теперь ось проходит через конец стержня 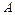 . Тогда при определении момента инерции стержня пределы интегрирования будут иными:
. Тогда при определении момента инерции стержня пределы интегрирования будут иными:
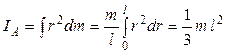 . (2)
. (2)
Этот результат можно получить также с использованием теоремы Гюйгенса–Штейнера. Действительно,
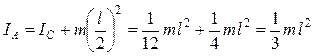 .
.
Следует заметить, что формулы (1) и (2) не применимы к стержню конечной толщины.
Ответ: 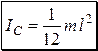 ,
, 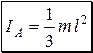 .
.
Задача 4.2. Определить угловое ускорение блока радиусом 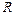 с моментом инерции
с моментом инерции 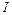 , через который перекинута нить с грузами массой
, через который перекинута нить с грузами массой 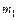 и
и 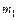 . Трением пренебречь.
. Трением пренебречь.
Дано: Решение:
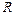
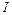
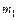
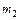
| Ранее мы рассматривали движение тел, перекинутых через блоки (задача 2.2.), пренебрегая массой блоков. Теперь, в данной задаче, приведен момент инерции блока, это означает, что он обладает массой. Тогда помимо уравнений движений для грузов 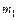 и и 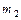 необходимо необходимо
|
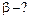
| записать уравнение движения блока. Таким уравнением будет уравнение динамики вращательного движения, так |
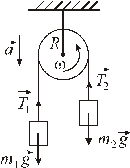
как блок будет вращаться под действием сил 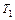 и
и 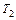 вокруг своей оси, проходящей через центр масс.
вокруг своей оси, проходящей через центр масс.
Пусть 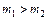 , тогда груз
, тогда груз 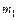 будет опускаться, а блок вращаться против часовой стрелки (см. рис.). В результате получим следующую систему уравнений:
будет опускаться, а блок вращаться против часовой стрелки (см. рис.). В результате получим следующую систему уравнений:
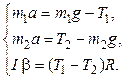
Здесь учтено, что нить нерастяжима, поэтому грузы 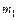 и
и 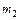 будут двигаться с одинаковым по модулю ускорением.
будут двигаться с одинаковым по модулю ускорением.
Учитывая связь между линейным и угловым ускорениями 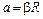 , запишем систему в виде:
, запишем систему в виде:
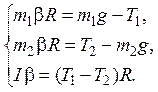
Исключая неизвестные 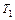 и
и 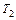 , получим ответ:
, получим ответ:
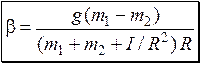 .
.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 5648; Нарушение авторских прав?; Мы поможем в написании вашей работы!