Динамика поступательного движения

Динамика изучает механическое движение тел в связи с действующими на них силами. Сила, действующая на тело, является мерой взаимодействия его с окружающими объектами и приводящая к изменению скорости движущегося тела. В основе механики лежат 3 закона Ньютона.

1 закон Ньютона: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие другого тела не выведет его из этого состояния.

2 закон Ньютона: ускорение, приобретаемое телом под действием внешнего воздействия, прямо пропорционально величине этого воздействия и обратно пропорционально массе тела:

.

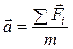3 закон Ньютона: два тела действуют друг на друга с силами, равными по величине и противоположными по направлению:

.

Количеством движения или импульсом тела массой 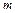, движущегося со скоростью 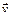, называется величина

.

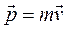Второй закон Ньютона можно представить в общей форме

,

то есть изменение количества движения тела пропорционально действующей силе и происходит в направлении этой силы.

Сила трения скольжения пропорциональна силе нормального давления 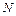, с которой одно тело действует на другое:

,

где 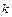– коэффициент трения.

Закон всемирного тяготения: любые два тела (материальные точки) притягиваются друг к другу с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними:

,

где 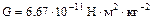– гравитационная постоянная.

Задача 2.1. На наклонной плоскости с углом к горизонту 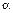находится тело массой 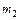, связанное невесомой нитью с телом массой 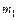. Найти ускорение этих тел, если известно, что тело 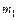опускается. Трением в блоке пренебречь. Коэффициент трения тела 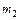о наклонную плоскость равен .

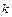Дано: Решение:

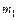
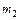
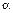
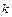
	Изобразим все силы, действующие на каждое тело. Тогда уравнения движения (второй закон Ньютона) каждого тела будут иметь вид: , .
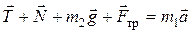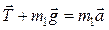	Здесь учтено, что нить нерастяжима, поэтому ускорения тел по модулю будут равны. Вектор ускорения направим, как показано на рисунке.

Для описания движения первого тела выберем направление оси системы отсчета вертикально вниз, а для второго тела направление одной из осей возьмем вдоль наклонной плоскости, а другой – перпендикулярно. Тогда уравнения движения в проекциях на координатные оси будут выглядеть следующим образом:

,

,

.

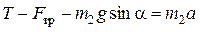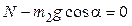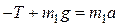Сила трения скольжения равна при этом

.

Тогда можно написать

,

.

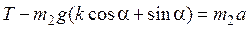Складывая два последних уравнения, получим

.

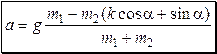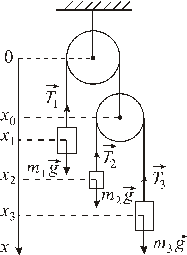
Задача 2.2. Определить ускорения грузов массам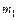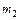и , и в системе блоков, показанной на рисунке. Массой блока и нитей пренебречь. Трение отсутствует.

Дано: Решение:

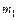
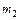
	Изобразим все силы, действующие на каждое тело. Ось 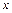системы отсчета направим вертикально вниз, начало отсчета возьмем в центре верхнего блока. Тогда уравнения движения каждого тела в проекциях на выбранную ось будут иметь вид
	: ,

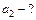
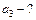
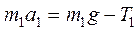, (1)

.

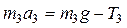Так как в условиях задачи данные приведены в общем виде, мы не можем сразу определить характер движения каждого тела, какое тело будет опускаться, а какое подниматься. Поэтому ускорения в левых частях системы (1) оставляем в общем случае, потому что оно является не причиной, а следствием движения. Если при решении задачи ускорение какого-либо тела даст положительную величину, то оно будет двигаться вниз по оси 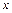, если отрицательную – то против оси .

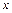По условию задачи трение отсутствует, массу блоков и нити не учитываем, нить считаем нерастяжимой. Тогда для сил натяжения нитей можно записать следующие соотношения:

, .

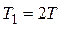Тогда систему (1) запишем в виде:

(2)

Имеем систему трех уравнений с четырьмя неизвестными. Для однозначного его решения необходимо еще одно уравнение. Для его получения поступим следующим образом. Запишем выражение для длины каждой нити с учетом того, что длины нитей постоянны. Из рисунка видно, что

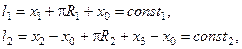(3)

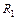где и 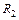– радиусы блоков. Взяв вторые производные каждого уравнения системы (3), с учетом 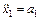, , 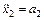, , 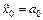где – ускорение нижнего подвижного блока, получим соотношение, связывающее ускорения грузов:

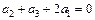. (4)

Решая совместно (2) и (4), получим ответ:

, ,

.

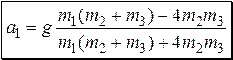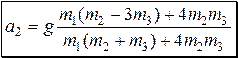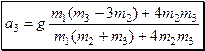Дата добавления: 2014-10-22