Виды событий

ЛЕКЦИЯ № 2

Тема: ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

План лекции:

1. Виды событий.

2. Классическое определение вероятности.

3. Применение комбинаторных соединений к вычислению вероятности события по классическому определению.

Опр.: Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.

Опр.: Случайные явления – это реальные явления, которые при многократном воспроизведении одного и того же опыта могут протекать по-разному.

Опр.: Опыт (испытание, эксперимент) – это комплекс условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.

Опр.: Случайное событие – любой факт, который в результате опыта может произойти или не произойти. Случайные события будем обозначать заглавными латинскими буквами: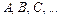

Замечание: Случайное явление – результат реального опыта, а случайное событие – это результат мысленного опыта, проведенного в идеальных условиях. Случайное событие – это математическая модель случайного явления.

Примеры случайных событий:

– выпадение «герба» в результате подбрасывания монеты;

– выигрыш автомобиля по лотерейному билету;

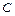– попадание в цель в результате выстрела;

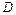– выпадение более 1000 мм осадков в данном географическом пункте за определенный год.

Некоторые события обладают свойством обязательно наступать всякий раз, когда производится опыт. Такие события будем обозначать греческой буквой .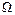

Опр.: Если в результате опыта событие обязательно должно произойти, оно называется достоверным.

Пример достоверного события 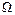– выпадение не более 6 очков в результате подбрасывания игральной кости.

Опр.: Если в результате опыта событие не может произойти, оно называется невозможным. Невозможное событие обозначается знаком Ø.

Например, Ø – в результате подбрасывания обычной игральной кости выпадает 10 очков. Это событие никогда не произойдет.

Опр.: Два события называются совместными, если в результате одного опыта они оба могут наступить, и несовместными, если в результате одного опыта они не могут наступить вместе.

Задача 2.1: Выяснить попарную совместность или несовместность следующих событий:

– появление «туза» в результате извлечения одной карты из колоды;

– появление «десятки» в результате извлечения одной карты из колоды;

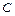– появление карты красной масти в результате извлечения одной карты из колоды.

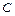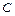Решение: События и – несовместны, поскольку в результате извлечения из колоды одной карты нельзя получить «туза», являющегося в то же время «десяткой»; и – совместны, так как в результате извлечения из колоды одной карты можно получить «туза» красной масти, например, бубнового; и – совместны, так как можно извлечь «десятку» красной масти.

Замечание 1: Условия опыта необходимо указывать точно, например, если в последнем примере не оговорить, что извлекается одна карта, то события и будут совместны.

Замечание 2: Понятие совместности можно распространить на любое конечное число событий.

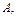
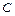Например, по условиям последнего примера, поскольку в колоде нет карты красной масти, являющейся и «тузом» и «десяткой» одновременно, то можно говорить о том, что и – несовместны в совокупности.

Опр.: Несколько событий называются равновозможными, если по условиям симметрии в результате повторений опыта ни одно из них не должно происходить чаще других.

Например, извлечение туза, валета, короля или дамы из колоды карт либо появление герба или решки при подбрасывании монеты – события равновозможные.

Замечание: Равновозможные события не могут появляться иначе, чем в испытаниях, обладающих симметрией возможных результатов опыта.

Задача 2.2: Являются ли следующие события равновозможными:

– выпадение 1-го очка в результате подбрасывания игральной кости;

– выпадение 2-х очков в результате подбрасывания игральной кости;

– выпадение 3-х очков в результате подбрасывания игральной кости;

– выпадение 4-х очков в результате подбрасывания игральной кости;

– выпадение 5-ти очков в результате подбрасывания игральной кости;

– выпадение 6-ти очков в результате подбрасывания игральной кости?

Решение: Если считать, что игральная кость является идеально симметричной, то все эти события равновозможны. В дальнейшем будем считать все кости идеально симметричными.

Ответ: являются.

Задача 2.3: Являются ли равновозможными события:

– выпадение четного количества очков в результате подбрасывания игральной кости;

– выпадение нечетного количества очков в результате подбрасывания игральной кости?

Решение: Как четное, так и нечетное количество очков можно получить тремя способами, поэтому симметричность игральной кости обеспечивает равновозможность событий.

Ответ: являются.

Задача 2.4: Являются ли равновозможными события:

– появление «герба» в результате подбрасывания монеты;

– появление «решки» в результате подбрасывания монеты?

Решение: Если считать, что монета является идеально симметричной, то события равновозможны. В дальнейшем будем считать все монеты идеально симметричными.

Ответ: являются.

Опр.: Если в результате опыта обязательно происходит одно и только одно из нескольких событий, то говорят, что эти события составляют полную группу. Будем обозначать полную группу из 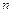событий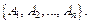

Задача 2.5: Пользуясь условиями задачи 2.1, выяснить, составляют ли рассматриваемые совокупности событий полные группы.

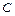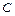Решение: События и не составляют полной группы, поскольку в результате извлечения из колоды одной карты можно получить карту, не являющуюся ни «тузом», ни «десяткой»; и также не составляют полной группы, поскольку можно извлечь карту черной масти, не являющуюся «тузом»; и не составляют полной группы по той же причине; кроме событи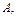й и 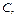результатом опыта может быть извлечение карты черной масти, причем не «туза» и не «десятки», то есть они также не составляют полной группы.

Легко видеть, что в каждой из задач 2.2 – 2.4 события составляют полную группу.

Замечание: Очевидно, что события в полной группе несовместны попарно (а значит, и в совокупности). В частном случае, если полную группу образуют два события, то они называются противоположными, их будем обозначать и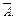

В задачах 2.3 и 2.4 рассмотрены противоположные события.

Задача 2.6: Событие – появление хотя бы одного «туза» в результате извлечения трех карт из колоды. Сформулировать событие, противоположное для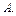

Решение: Появление хотя бы одного «туза» означает появление одного или более чем одного «туза», тогда 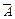– отсутствие «тузов» среди трех извлеченных из колоды карт.

Задача 2.7: Событие – выпадение не более чем двух очков в результате подбрасывания игральной кости. Сформулировать событие, противоположное для события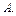

Решение: Выпадение не более чем двух очков означает выпадение двух или менее чем двух очков, тогда 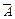– выпадение более чем двух очков в результате подбрасывания игральной кости.

Опр.: Если все возможные результаты опыта можно представить в виде полной группы равновозможных событий, то их совокупность называют множеством элементарных исходов опыта. Элементарные исходы опыта будем обозначать греческой буквой 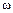с индексами.

Выше показано, что в задаче 2.2 рассматриваются равновозможные события, составляющие полную группу, которые по определению будут составлять пространство элементарных исходов опыта, состоящего в подбрасывании игральной кости:

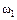– выпадение 1-го очка; 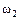– выпадение 2-х очков;

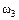– выпадение 3-х очков; 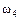– выпадение 4-х очков;

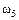– выпадение 5-ти очков; 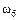– выпадение 6-ти очков.

Аналогично, события в задачах 2.3 и 2.4 составляют пространства элементарных исходов соответствующих опытов. Отметим, что в задачах 2.6 и 2.7 рассмотрены противоположные события, которые также составляют полные группы, но они не являются равновозможными, поэтому не могут составлять пространства элементарных исходов соответствующих опытов.

Опр.: Элементарный исход опыта называется благоприятным для события 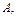если в результате опыта при появлении этого исхода обязательно наступает событие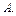

Задача 2.8: – выпадение числа очков, кратного трем, в результате подбрасывания игральной кости. Выделить в пространстве элементарных исходов опыта, описанных в задаче 2.2, благоприятные исходы для события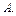

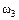Решение: Так как число очков, кратное трем, выпадет только в случае появления трех или шести очков, то благоприятными для события являются исходы и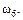

Дата добавления: 2014-10-23