Системы сил

Условия равновесия произвольной пространственной

Произвольной пространственной называется такая система сил, линии действия сил которой произвольно расположены в пространстве.

Определение реакций связей

С-3. Произвольная пространственная система сил.

Векторная форма условия равновесия: для равновесия произвольной пространственной системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы её главный вектор был равен нулю и главный момент системы сил относительно произвольной точки был равен нулю: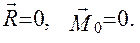

Аналитическая форма условия равновесия:

- для равновесия произвольной пространственной системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трёх координатных осей были равны нулю, и суммы моментов всех сил системы относительно каждой из этих осей были равны нулю:

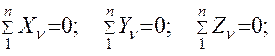
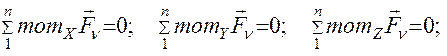
3.7.2. Задача С3

Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником) в точке А, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С3.0 — С3.7) или же двумя подшипниками в точках А и В и двумя невесомыми стержнями 1 и 2 (рис. С3.8, С3.9); все стержни прикреплены к плитам и к неподвижным опорам шарнирами.

Размеры плит указаны на рисунках; вес большей плиты Р₁ = 5 кН, вес меньшей плиты Р₂ = 3 кН. Каждая из плит расположена парал­лельно одной из координатных плоскостей (плоскость ху — горизон­тальная).

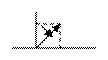
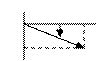
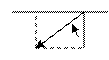
На плиты действуют пара сил с моментом М=4 кН-м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направле­ния и точки приложения указаны в табл. С3; при этом силы F₁ и F₄ ле­жат в плоскостях, параллельных плоскости ху, сила F₂ — в плоскости, параллельной xz, и сила F ₃ — в плоскости, параллельной yz. Точки приложения сил (D, Е, Н, К) находится в углах или в серединах сторон плит.

Определить реакции связей в точках A и В и реакцию стержня (стержней). При подсчетах принять а = 0,6 м.

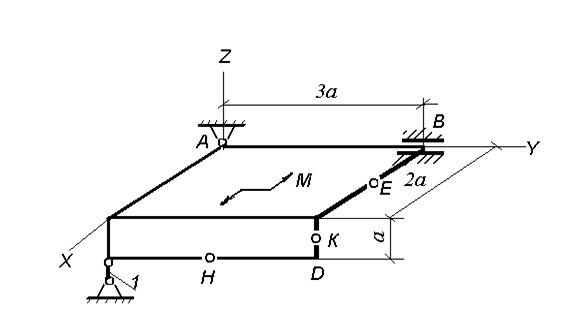
Рис. С 3.0

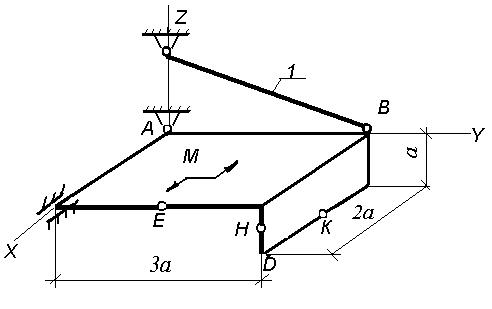
Рис. С 3.1

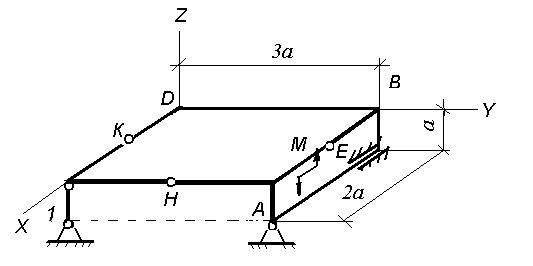
Рис. С 3.2

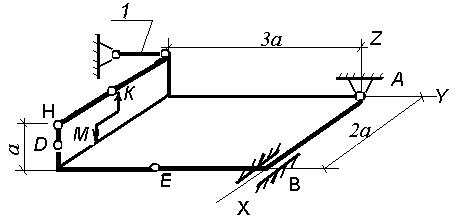
Рис. С 3.3

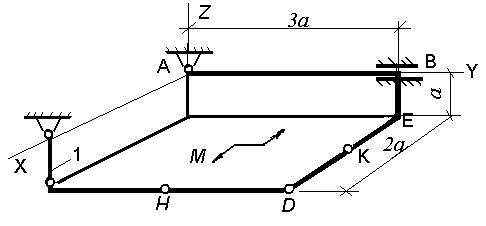
Рис.С 3.4.

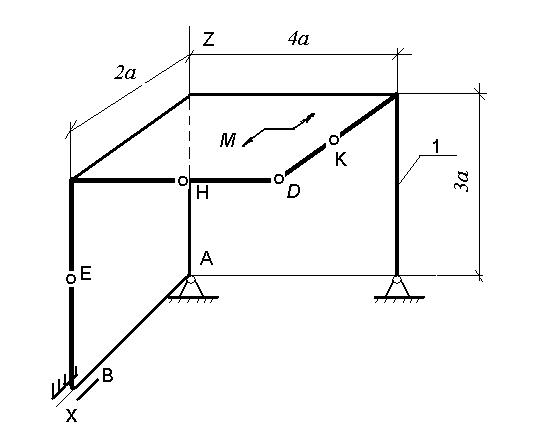
Рис. С 3.5

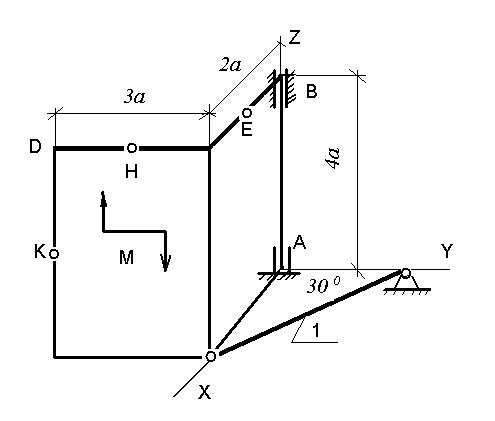
Рис. С 3.6

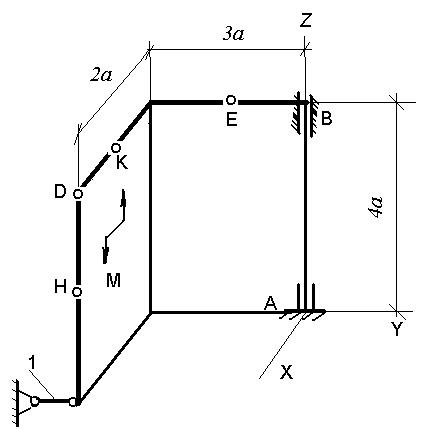
Рис. С 3.7

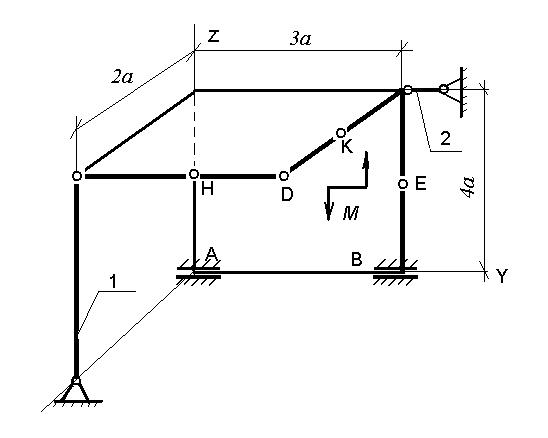
Рис. С 3.8

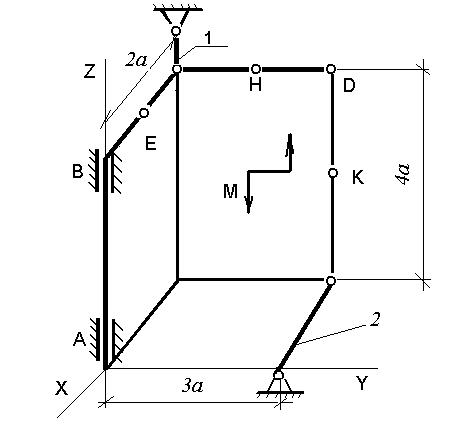
Рис. С3.9

Указания. Задача С3 — на равновесие тела под действием произ­вольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляю­щие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) — две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении мо­мента силы F часто удобно разложить ее на две составляющие F' и F", параллельные координатным осям (или на три); тогда, по теореме Вариньона, m_x(F) = m_x(F') + m_x(F") и т.д.

Таблица С-3

Сила	Y Z α2 Z Y F1 F2 α3 Y X α1 X F3 F4 α4 X
F1=6 кН	F2=8 кН	F3=10 кН	F4=12 кН
Номер условия	Точка прило- жения	α1 – град.	Точка прило- жения	α2 – град.	Точка прило- жения	α3 – град.	Точка прило- жения	α4 – град.
	E		H		-	-	-	-
	-	-	D		E		-	-
	-	-	-	-	K		E
	K		-	-	D		-	-
	-	-	E		-	-	D
	H		K		-	-	-	-
	-	-	H		D		-	-
	-	-	-	-	H		K
	D		-	-	K		-	-
	-	-	D		-	-	H

Дата добавления: 2014-10-31