
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример К-1а
|
|
|
|
Скалярное касательное ускорение точки в данный момент времени равно первой производной от скалярной скорости по времени или второй производной от естественной координаты по времени.
Модуль нормального ускорения точки в данный момент времени определяется выражением:
 , где ρ – радиус кривизны траектории в точке.
, где ρ – радиус кривизны траектории в точке.
Касательное ускорение направлено по касательной к траектории, нормальное – по главной нормали в сторону вогнутости траектории.
Касательное ускорение характеризует изменение модуля скорости, а нормальное – изменение направления скорости.
Ускорение точки при движении по любой траектории равно сумме касательного и нормального ускорения:
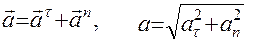 .
.
Классификация движений точки по ускорениям:
1.  - движение неравномерное, прямолинейное;
- движение неравномерное, прямолинейное;
2. 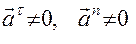 - движение неравномерное, криволинейное;
- движение неравномерное, криволинейное;
3.  - движение равномерное, криволинейное;
- движение равномерное, криволинейное;
4. 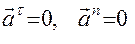 - движение равномерное, прямолинейное.
- движение равномерное, прямолинейное.
4.1.1 Задача К-1. Определение скоростей и ускорений точки по заданным уравнениям ее движения.
Под номером К1 помещены две задачи К1а и К1б, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1. 0 — К1. 9, табл. KI; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у = f2(t), где хну выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х = f1(t) указана непосредственно на рисунках, а зависимость
y = f2(t) дана в табл. К1 (для рис. 0—2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1 — С3, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 — по последней.
Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону S = f(t), заданному в табл. К1 в столбце 5 (S в метрах, t в секундах), где S = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1=1 с. Изобразить на рисунке векторы V и a, считая, что точка в этот момент находится в положении М, а положительное направление отсчета S — от А к М.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.
В задаче все искомые величины нужно определить только для момента времени t1 = 1 с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:

 ;
;
 .
.
Таблица К1
| Номер условия | y = f2(t) | S = f(t) | ||
| Рис.0-2 | Рис.3-6 | Рис. 7-9 | ||
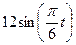
| 2t2+2 | 
| 
| |
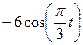
| 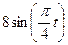
| 
| 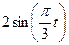
| |
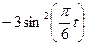 
| (2+t)2 | 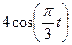
| 6t-2t2 | |

| 2t3 | 
| 
| |

| 
| 
| 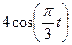
| |

| 2-3t2 | 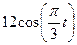
| 
| |
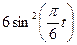
| 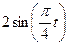
| 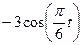
| 3t2-10t | |

| (t+1)3 | 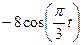
| 
| |

| 2-t3 | 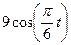
| 
| |
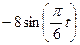
| 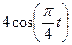
| 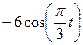
| 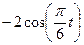
|
|

Дано: уравнения движения точки в плоскости XOY:
x=12sin(πt/6), y=4cos(πt/6), где x, y – в сантиметрах, t – в секундах.
Определить: уравнение траектории точки; для момента времени t1=1с найти скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение
1. Для определения уравнения траектории точки исключим из данных уравнений движения параметр t:
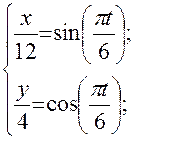
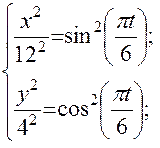

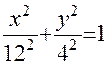 - уравнение траектории точки – эллипс с полуосями 12 см и 4 см (рис. К -1).
- уравнение траектории точки – эллипс с полуосями 12 см и 4 см (рис. К -1).
2. Определим положение точки на траектории в момент времени t1=1с:
x1=12sin(πt/6)=6(см), y1= 4cos(πt/6)= 3,48 (см).
3. Скорость точки находим по её проекциям на координатные оси:
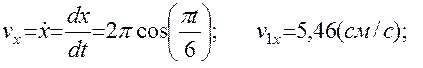
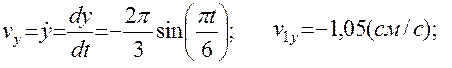
 , при t1=1с
, при t1=1с 
4.Аналогично найдём ускорение точки при t1=1с:
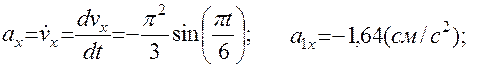

5. Находим касательное ускорение точки, зная численные значения всех величин, входящих в правую часть выражения:
 при t1=1с
при t1=1с 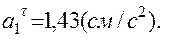
6. Нормальное ускорение точки определяем по формуле 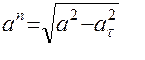 , подставляя известные численные значения. При t1=1с получим
, подставляя известные численные значения. При t1=1с получим 
7. Определяем радиус кривизны траектории: ρ=v2/an при t1=1с ρ1=24,93 (см).
Ответ: v1=5,56 (cм/c); a1=1,89 (cм/c2); a1τ=1,43 (cм/c2); a1n=1,24 (cм/c2); ρ1=24,93 (см).
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 793; Нарушение авторских прав?; Мы поможем в написании вашей работы!


 0 Рис.К1.0 X 0 Рис.К1.1 X 0 Рис.К1.2 X
Y Y Y
B B B
0 Рис.К1.0 X 0 Рис.К1.1 X 0 Рис.К1.2 X
Y Y Y
B B B

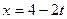
 0 0 0
Рис.К1.3 X Рис.К1.4 X Рис.К1.5 X
Y Y Y
B B B
0 0 0
Рис.К1.3 X Рис.К1.4 X Рис.К1.5 X
Y Y Y
B B B
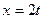
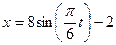
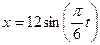 0 Y 0 Y 0 Y
Рис.К1.6 Рис.К1.7 Рис.К1.8
Y
B
0 Y 0 Y 0 Y
Рис.К1.6 Рис.К1.7 Рис.К1.8
Y
B
 0 Y
Рис.К1.9
0 Y
Рис.К1.9