Вывод формулы для нормального и тангенциального ускорения

Кинематика

Информационно-справочные и поисковые системы

Базы данных, Интернет-ресурсы,

1. Единое окно доступа к образовательным ресурсам. Электронная библиотека [Электронный ресурс]: инф. система. – М.: ФГАУ ГНИИ ИТТ "Информика", 2005-2012. – Режим доступа: //www. http://window.edu.ru, свободный. – Загл. с экрана (дата обращения 11.04.2012)

2. Интернет-университет информационных технологий – дистанционное образование – INTUIT.ru [Электронный ресурс]: офиц. сайт. – М.: Открытые системы, 2003-2011. - Режим доступа: http://www.intuit.ru, свободный. - Загл. с экрана (дата обращения: 17.05.2012).

3. Консультант Плюс 1997-2012 [Электронный ресурс]: справочно-поисковая система.- Режим доступа: http://www.consultant.ru/?utm_source=sps

4. Поисковые системы: Google, Yandex, Rambler

5. Электронная библиотечная система «Издательство «Лань» [Электронный ресурс] – Режим доступа: www URL: http://e.lanbook.com/ - 25/08/2010

6. Электронная библиотечная система «Университетская библиотека онлайн» [Электронный ресурс] – Режим доступа: www URL: http://www.biblioclub.ru/ - 25/08/2010

При любом движении точки, кроме равномерного прямолинейного движения, скорость точки изменяется. Для характеристики быстроты изменения скорости 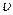точки в механике вводится векторная физическая величина, называемая ускорением.

Ускорением называется вектор а, равный первой производной по времени t от скорости 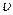этой точки;

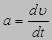
Ускорение точки равно также второй производной по времени от радиус-вектора r этой точки:

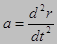
Поскольку вектор ускорения при криволинейном движении сориентирован по отношению к скорости под произвольным углом, то разложим его на нормальную и тангенциальную составляющие:

a = a _n + a _t = a_n· n + a_t ·t.

Определим величину, направление и роль в изменении скорости нормального ускорения. Предположим, что:

a = a _n.

Тогда:

d u = a ·dt = a _n·dt.

Таким образом, вектор приращения скорости параллелен вектору нормального ускорения. Поскольку нормаль n перпендикулярна t, а, следовательно, и вектору скорости, то всегда вектор приращения скорости также перпендикулярен v. В данном случае годограф представляет из себя окружность, и скорость изменяется только по направлению, сохраняясь неизменной по величине. Следовательно, направление вектора приращения скорости совпадает с вектором n.

Величину вектора a_n можно рассчитать из простых геометрических соображений.

Путь ds, пройденный частицей за время dt, можно рассчитать двумя способами:

ds = u · dt;

ds = R·da.

Учтя, что угол du = u·da, получим:

a_n = du/dt = u²/R

или в векторном виде

a _n = u²/R· n.

Нормальное ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения равен

a _n = u²/R· n.

Определим величину, направление и роль в изменении скорости тангенциального ускорения. Предположим, что a = a _t.

Тогда:

d u = a ·dt = a _t·dt.

Следовательно, в данном случае вектор приращения скорости параллелен вектору тангенциального ускорения. Вектора приращения скорости и тангенциального ускорения также направлены вдоль t.

Поскольку направление вектора скорости не изменяется с течением времени, то модуль приращения вектора скорости |d u | равен приращению модуля вектора скорости d| u | = du и
a_t = du/dt.

Тангенциальное ускорение характеризует изменение скорости по величине. Вектор тангенциального ускорения равен a _t = du/dt· t.

В общем случае, когда скорость изменяется по величине и направлению значение модуля вектора ускорения равно:

.

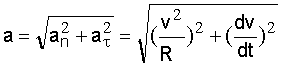Сам вектор полного ускорения состоит из суммы двух слагаемых:

a = d(u·t)/dt = du/dt· t + u·d t /dt.

Первое слагаемое представляет собой его тангенциальную составляющую, а второе - нормальную составляющую, причем d t /dt = u/R ·n.

Нормальное ускорение точки характеризует быстроту изменения направления вектора скорости точки. Нормальное ускорение направлено всегда к центру кривизны траектории, так что его проекция на главную нормаль nне может быть отрицательной:

По этой причине нормальное ускорение точки часто называют также центростремительным ускорением. Нормальное ускорение точки равно нулю только в том случае, если точка движется прямолинейно.

Дата добавления: 2014-11-06