Не красный. Не круг

Формирование графического навыка

Параллельно изучению следующего раздела программы проводится подготовительная и основная работа по обучению написанию цифр. Материал для нее находится в конце первой и второй частей учебника-тетради.

Учитель самостоятельно определяет объем соответствую­щей работы на уроке.

Особенность предлагаемой методики заключается в ис­пользовании дефектных образцов и в требовании оценки уча­щимися качества написанных ими знаков.

Так, при обучении написанию цифры 1 учитель записывает ее на доске. Учащиеся называют ее. Сообщается, что при пись­ме цифр нужно стараться вести ручку безотрывно, проводить только одну линию в одном направлении.

Вместе с детьми определяется, что цифру 1 нужно начинать писать с «носика». Далее учитель показывает маршрут движе­ния внутри клетки, поясняя его.

На тренировочной странице учебника учащиеся обводят образцы цифры. Обращается внимание на то, что среди образ­цов есть неправильные — «ловушки». Их обводить не надо. На этот раз они отмечены точками. Важно самим не сделать таких неточностей в написании.

При написании других цифр дети должны сами отмечать точкой неправильные образцы. Затем при самостоятельном написании цифр время от времени предлагается «поймать точ­кой» свою неточность, а правильно написанные цифры отме­тить положительной оценкой — «знаком улыбки»

Можно предлагать оценивать сначала каждую цифру, потом выборочно: «Найдите и отметьте три самые правильные ци­фры, три самые неточные. Теперь попробуйте написать циф­ры без этих неточностей».

Проверяя работу ученика, учитель одобряет ее именно за правильность самооценки, а не за качество написанных цифр. (Как знак одобрения может быть использована та же «улыбка», проставленная на поле рядом со строчкой.)

В этом случае дети охотно ищут свои ошибки, а значит, по­степенно избавляются от них.

В этом разделе дети знакомятся с отрицательной формой описания предметов.

1. Вводная задача. Игра «Угадай фигуру». На фланелеграфе и на партах набор фигур, различающихся по форме и цвету.

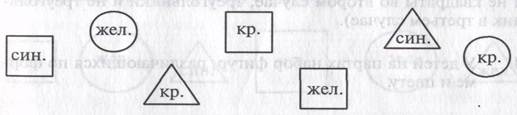
Как и раньше, требуется угадать загаданную учителем фигуру за наименьшее число вопросов. Так как фигуры отли­чаются только цветом и формой (и не расположены в ряд), то «хорошими» будут вопросы о форме и цвете фигур. Однако теперь учитель дает ответы в отрицательной форме. Напри­мер:

Д. Какой формы эта фигура?

У. Она не квадрат.

Д. Какого цвета эта фигура?

У. Она не красного цвета.

После каждого ответа учителя дети убирают лишние фи­гуры. Так, после первого ответа убираются квадраты, а после второго — фигуры красного цвета. В результате остаются толь­ко желтый круг и синий треугольник. Теперь можно задать лю­бой вопрос о цвете или форме, и любой ответ (в отрицательной или положительной форме) позволит отгадать искомую фи­гуру.

2.* (Более трудный вариант игры «Угадай фигуру».) Задания аналогичны предыдущему, только загадывают фигуру и отвечают на вопросы в отрицательной форме сами дети. Используются небольшие наборы фигур, отличающихся только цветом и формой.

3. Учебник, ч. 1, с. 6. Упр. 1 — 3. В упр. 1 надо нарисовать две фигуры, которые отличаются от заданной по одному признаку и не отличаются по другому.

В упр. 2 во всех случаях фигуры разбиты на группы по фор­ме. Только в первом случае разбиение на группы отвечает на вопрос о форме фигур в положительной форме (квадраты, круги, треугольники), а в других — в отрицательной (квадраты и не квадраты во втором случае, треугольники и не треуголь­ник в третьем случае).

4. У детей на партах набор фигур, различающихся по фор­ме и цвету.

Учитель предлагает описание фигуры, а дети должны вы­брать из своего набора подходящую фигуру:

«Покажите красную фигуру, но не треугольник». (Крас­ный круг.)

«Покажите не желтый квадрат». (Синий квадрат.)

«Покажите желтую фигуру, но не круг». (Желтый квадрат, желтый треугольник.)

И т. п.

1.5. Размер. Больше? Меньше?

В этом разделе уточняются представления о размере. Выявляется относительный характер этого признака. В отли­чие от цвета и формы, нельзя определить размер отдельно­го предмета, т. е. сказать, маленький он или большой. Что­бы это сделать, надо сравнить этот предмет с другим: если предмет маленький, то только по сравнению с другим — большим. Таким образом, различить (сравнить) предметы по размеру — это значит определить, какой из них больше, а ка­кой меньше (установить между ними отношение «больше — меньше»).

Кроме того, в этом разделе рассматривается упорядочива­ние предметов по размеру, т. е. расположение их в ряд по воз­растанию или убыванию.

1. Вводное задание.

На фланелеграфе горизонтально расположены фигуры, раз­личающиеся по форме, цвету и размеру.

Дети должны описать фигуры по их расположению.

У. Какие фигуры находятся правее синего треугольника?

Д. Большой красный квадрат, большой зеленый круг, ма­ленький желтый треугольник.

У. Какие фигуры находятся слева от синего треугольни­ка?

Д. Маленький красный квадрат, большой желтый круг.

У. Какие фигуры находятся между синим треугольником и зеленым кругом?

Д. Большой красный квадрат.

Учитель убирает левый квадрат и добавляет справа красный квадрат большего размера, чем оставшийся квад­рат.

После этого он повторяет последний вопрос: «Какие фигуры находятся между синим треугольником и зеленым кругом?»

Некоторые дети сразу замечают противоречивость ситуа­ции и затрудняются с ответом, другие дают правильный в но­вой ситуации ответ: «Маленький красный квадрат». Учитель драматизирует ситуацию:

У. Как же так? Сначала вы об этой фигуре сказали, что это большой красный квадрат, а теперь что это маленький крас­ный квадрат. Так какой же на самом деле это квадрат, боль­шой или маленький?

В ходе обсуждения детьми этой проблемы выявляется, что в обоих случаях фигура описана правильно, поскольку дан­ный квадрат большой по сравнению с убранным (первый слу­чай) и маленький по сравнению с добавленным (второй слу­чай). Точнее сказать, что данный квадрат больше убранного и меньше добавленного.

2. На фланелеграфе одна фигура (например, желтый круг).

У. Какого цвета эта фигура?

Д. Желтого.

У. Какой она формы?

Д. Круг.

У. А какого она размера?

Оказывается, что нельзя ответить на этот вопрос. Учитель добавляет еще одну фигуру (например, зеленый круг больше­го размера).

У. А теперь вы можете ответить?

Д. Да, она маленькая.

Учитель добавляет еще одну фигуру (например, синий круг, который меньше желтого).

У. А теперь что вы скажете о ее размере: она маленькая или большая?

По мере поступления детских ответов учитель добавляет, если нужно, еще фигуры (круги), вынуждая детей изменять

(уточнять) свои ответы, например: Желтый круг меньше зе­леного и больше синего. В итоге делается следующий вывод: «Про одну фигуру нельзя сказать, большая она или малень­кая. Определить размер фигуры можно, только сравнив ее с другой: одна фигура больше или меньше другой, а не одна боль­шая, а другая маленькая».

3. Учебник, ч. 1, с.7. Упр.1.

4. У детей наборы из пяти треугольников, отличающихся друг от друга цветом и размером.

Один ребенок работает у доски, а остальные за парта­ми. Учитель предлагает детям взять зеленый треугольник и положить его перед собой. Затем взять синий треугольник и сравнить его с зеленым. Выясняется, что синий треугольник больше зеленого. Учитель предлагает положить синий треу­гольник справа от зеленого. После этого выбирается красный треугольник и сравнивается с зеленым и синим. Он больше зеленого треугольника и меньше синего. Учитель спрашивает у детей, куда его лучше положить. Лучше всего его положить между зеленым и синим треугольниками, тогда сразу видно, что он больше одного и меньше другого.

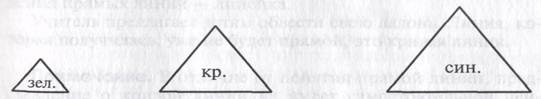
Далее с детьми обсуждается, как расположены треугольни­ки. Устанавливается, что треугольники расположены по порядку от меньшего к большему: чем больше, тем правее. После этого учитель предлагает поместить в этот ряд остав­шиеся треугольники. Дети делают это, обосновывая свои действия. Учитель может участвовать в этой работе, предла­гая неправильные варианты размещения треугольников и вы­нуждая детей отвергать их.

В заключение учитель предлагает детям по-другому распо­ложить треугольники - наоборот, от большего к меньшему.

5.Учебник, ч. 1,с. 6. Упр. 2, 3.

Дата добавления: 2014-11-16