Сравнение величин с помощью посредника

Введение числа(10-12 уроков)

В этой теме рассматриваются ситуации, в которых освоен­ные способы непосредственного сравнения величин не подхо­дят, например если предметы разделены в пространстве или во времени либо различны по форме.

Для ее решения приходится прибегнуть к некоторой другой величине — мерке (условной единице), которая повторяется в данной величине некоторое число раз. Таким образом, в пер­вую очередь выявляется операторный смысл числа: число вы­ступает как инструмент, позволяющий получить из одной ве­личины другие.

Далее рассматриваются различные способы фиксации ша­гов в процессе построения (отмеривания) величины и соответ­ствующие им формы представления чисел: с помощью меток (наиболее ранняя в истории форма числа), с помощью упоря­доченного ряда слов-числительных и замещающих их знач­ков-цифр (счет).

В заключение выявляется новый смысл числа — количе­ственный, когда число выражает результат измерения величины.

Сначала воспроизводится уже известный детям способ не­посредственного сравнения величин. Затем создается ситуа­ция, требующая использования посредника. Но пока это еще не число, а третья величина, с которой можно сравнить каж­дую из исходных величин по отдельности. На основании ре­зультатов этих двух сравнений можно сделать вывод об отно­шении между исходными величинами.

1. Учитель сообщает: «Сегодня вспомним, как нужно под­бирать равные величины». На столе учителя полоски картона, а в руке — брусок. Учитель стоит поодаль от сто­ла. Требуется найти полоску такой же длины, как брусок. Кто-то из детей направляется к учителю.

У. Но зачем ты идешь ко мне? Полоски находятся на столе!

Д. Нужен брусок, иначе не получится точно подобрать полоску. Брусок нужно приложить к полоскам.

Ученик выполняет задание. (На столе нужно иметь две явнонеравные длине бруска полоски, одну равную и одну слегка отличающуюся от нее.) Задание вполне знакомо и все дети знают, как нужно действовать.

2.На левом конце доски начерчен отрезок, длина которого обозначена буквой А, а на другом конце еще четыре от­резка с длинами Е, С, Н и Р (длины Е и Н явно неравны длине А; Р > А, С = А):

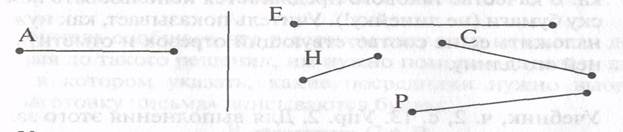
Учитель предлагает найти среди отрезков справа отрезок, длина которого равна длине А. Некоторые дети начнут угады­вать. На этом этапе отвергаются отрезки с длинами Е и Н, но остаются сомнения по поводу двух других отрезков. Учи­тель требует совершенно точного ответа и спрашивает, чем от­личается это задание от того, с которым только что легко и быстро справились. Выясняется, что здесь невозможно при­ложить левый отрезок к другим отрезкам. «Как быть?» Воз­можны попытки зафиксировать длину отрезка-эталона рука­ми. Учитель повторяет эти попытки, но при этом получает совсем другие результаты сравнения (специально меняя при переносе положение рук). Выясняется, что такой способ не будет точным, при переносе трудно сохранить положение рук неизменным.

Значит, надо заменить отрезок предметом такой же величи­ны (длины), но который можно переносить. Нужен посредник! Вероятно, кто-то из детей предложит воспользоваться линей­кой.

У. Но у меня линейки нет, а есть такие вещи: кружка, длин­ная веревочка, короткая бумажная полоска. Что нам поможет? Что послужит посредником?

В качестве посредника выбирается веревочка, с помощью которой и производится соизмерение длины А сначала с дли­ной Р, а затем с длиной С.

Далее учитель знакомит детей со специальным инструмен­том, который позволяет фиксировать длины, — циркулем. Снова производятся сравнения длин отрезков, но теперь уже с помощью циркуля.

В заключение еще раз подчеркивается, что открыт новый способ сравнения, и предлагается поупражняться в нем.

3. Учебник, ч. 2, с. 13. Упр. 1. Сначала устанавливается, что сравнить длины сторон фигур невозможно без посредни­ка. В качестве такового предлагается использовать поло­ску бумаги (не линейку!). Учитель показывает, как нужно наложить ее на соответствующий отрезок и отметить на ней его длину.

4.Учебник, ч. 2, с. 13. Упр. 2. Для выполнения этого зада­ния учитель предлагает использовать циркуль, а тем, у кого нет, воспользоваться полоской бумаги.

5. Учебник, ч. 2, с. 13. Упр. 3. Для его выполнения нужно воспользоваться материалом приложения. Все фигуры из него должны быть заранее вырезаны и сложены в кон­верты, которые следует выдавать детям на уроке. Дети должны выбрать среди фигур ту, которая имеет ту же пло­щадь, что и данная.

Дата добавления: 2014-11-16