Изменение величин

Действия с величинами (10-12уроков)

Критерии усвоения учебного материала

Учащиеся должны:

1) правильно выполнять предметное действие сравнения по заданному параметру. Например, когда учитель предлагает выяснить, равны ли книга и альбом по длине, ученик дол­жен правильно совместить эти предметы;

2) отвечая на вопрос о равенстве или неравенстве предметов, употребить название признака, например: «Эти предметы равны по длине» (а не «предметы равны»);

3) на просьбу показать два одинаковых по какому-то парамет­ру предмета уметь показать два предмета, отличающихся по другим параметрам, а не полностью идентичных;

4) уметь подобрать предметы к отношению, представленному отрезками, передать отношение величин отношением от­резков.

1. На столе у учителя два одинаковых сосуда, а на доске изображены два отрезка разной длины. Учитель сооб­щает, что отрезки рассказывают об объемах воды, которую детям нужно налить в эти сосуды, и предлага­ет сначала налить воду в сосуд, «о котором говорит вот этот отрезок» (показывается меньший отрезок), а уже затем в другой. Двое детей по очереди выходят к столу учителя и производят необходимые действия. Осталь­ные дети следят за правильным выполнением их рабо­ты. Выясняется, что не имеет значения, сколько воды наливать в каждый из сосудов, главное, чтобы объем воды в первом был меньше, чем во втором. В заключе­ние дети чертят в своих тетрадях соответствующие от­резки.

2.Уравнивание величин. На столе у учителя два одинако­вых сосуда, в которых налито разное количество воды. Дети замечают, что объем воды в одном сосуде больше, чем в другом, и фиксируют это на отрезках, которые чер­тятся в тетрадях и на доске.

После этого учитель сообщает, что нужно, чтобы в первом сосуде (с меньшим объемом воды) стало столько же воды, сколько во втором. (Это требование можно облечь в какой-ни­будь правдоподобный сюжет, например связанный с дозиров­кой какой-то жидкости.)

У. Что нужно для этого сделать?

Д. Нужно долить воду (жидкость) в первый сосуд.

Учитель добавляет в сосуд явно недостаточное количество воды. Дети говорят, что нужно налить больше. Тогда учитель требует более точного указания. Оказывается, что нужно долить то, чего не хватает, — разность. Учитель производит уравнение и предлагает учащимся выполнить такое же действие и отрезках. Дети дочерчивают (другим цветом) меньший от­резок (так, чтобы он стал равным с большим).

Обсуждение работы:

У. Вы выполнили то же самое действие, что и я?

Д. Да.

У. Я доливал воду. Разве вы что-нибудь доливали?

Д. Мы не доливали, а пририсовали.

У. Как же назвать наше общее действие?

Д. (При подсказке учителя.) Ивы, и мы увеличили, добави­ли разность (на отрезке показывается разность).

У. А в первый раз, что мной было сделано? Покажите это на отрезках.

Выясняется, что в первый раз учитель тоже увеличил (объ­ем), но добавил слишком мало (на отрезке показывается толь­ко часть разности).

3.Задание аналогично предыдущему, только теперь требу­ется уравнять большую величину до меньшей.

В ходе работы выясняется, что в этом случае надо уменьшить большую величину, причем не произвольным образом, а отнять (удалить) разность. На отрезках это можно показать, зачеркнув соответствующую часть более длинного отрезка, уменьшить его.

Взаключение рассматривается упр. 1 на с. 22 учебника (ч. 1).

Примечание. На данном этапе не рассматривается такой способ уравнивания, когда часть разности перемещается из одного объекта в другой. Сейчас важно, чтобы дети выделили действия увеличения и уменьшения и связали их в случае урав­нивания с необходимостью учета разности.

4.Учебник, ч. 1, с. 22. Упр. 2. Учитель поясняет детям, что на рисунке слева показано, какими были величины сна­чала, а справа, после стрелки, — что получилось после выполнения какого-то действия. Нужно догадаться, что сделали с величиной: увеличили или уменьшили. Свой ответ дети дают с помощью отрезков. Во второй паре рисунков способ соотнесения количеств (в данном случае — один к одному) показан не полностью, изображена только одна линия, связывающая куб с цилинд­ром. Поэтому, чтобы сравнить количества кубов и цилиндров, надо провести остальные линии.

5. Учебник, ч. 1, с. 23. Упр. 3. Выясняется, что объемы воды можно сделать равными либо первому объему, либо вто­рому, либо третьему. Нужно выполнить на чертежах все три варианта, поясняя, в каком случае производится уве­личение, в каком — уменьшение.

6.Учебник, ч. 1, с. 23. Упр. 4. Требуется уравнять количест­ва соответственно действию, показанному на чертеже. Выясняется, что надо уменьшить большее количество, в данном случае убрать (зачеркнуть) лишние круги.

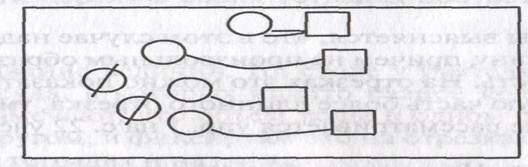
Оценивается представленная в учебнике работа трех учени­ков. Выясняется, что первый ребенок все выполнил правиль­но. Второй ребенок правильно выбрал действие уменьшения, но зачеркнул слишком много кругов, так что равенства не по­лучилось, что и показывается на чертеже.

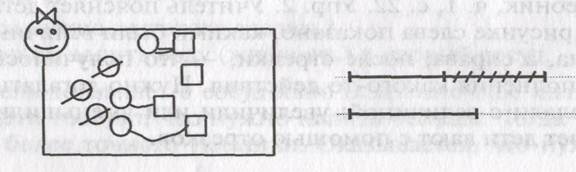
Третий ученик выполнил уравнивание, но сделал это, уве­личив количество квадратов.

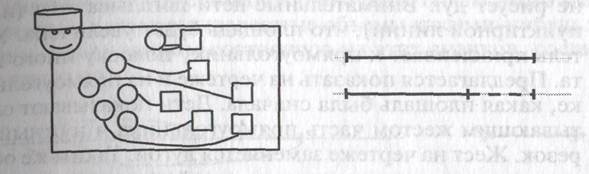
7. У учителя на столе сосуд, который не полностью запол­нен водой. Дети в своих тетрадях чертят отрезок, кото­рый будет рассказывать об объеме воды в сосуде. После этого учитель доливает в сосуд еще воды и предлагает де­тям показать это действие на чертеже (сделать то же са­мое, но с отрезком). Выясняется, что объем воды увели­чили и поэтому отрезок тоже надо увеличить.

На доске чертится отрезок, который будет рассказывать о длине «вот этой полоски» (учитель показывает, например, красную полоску, у каждого ребенка на парте есть такая же). После этого учитель зачеркивает часть отрезка и предлагает де­тям выполнить то же самое со своей полоской. Выясняется, что чертеж показывает, что надо уменьшить длину полоски, и дети отрезают часть полоски.

8. Учебник, ч. 1. с. 24. Упр. 5, 6.

9. У учителя крупа в пакете. Ее масса обозначается отрезком. Учитель отсекает часть отрезка, не делая зачеркивающих штрихов, и спрашивает, понятно ли при таком действии с чертежом, что нужно сделать с массой крупы. Кто-то из детей отсыпает часть крупы. Предлагается провести указ­кой по отрезку, соответствующему оставшейся части кру­пы. Затем вызываются два ученика. Они должны охваты­вающим жестом показать на чертеже, какая масса крупы была сначала (один ученик) и какая масса стала после уменьшения (другой ученик). Затем предлагается вместо рук охватить нужные отрезки дугами. Учитель рисует дугу для большего отрезка, а кто-то из детей — для меньшего.

10.Учитель показывает прямоугольник и делает чертеж на доске, в котором увеличивает исходный отрезок, но пока не рисует дуг. Внимательные дети догадываются (и без пунктирной линии), что площадь будет увеличена. Учи­тель приклеивает к прямоугольнику полоску иного цве­та. Предлагается показать на чертеже и на прямоугольни­ке, какая площадь была сначала. Дети показывают охва­тывающим жестом часть прямоугольника и нужный от­резок. Жест на чертеже заменяется дугой. Таким же обра­зом показывается жестами и дугой конечная площадь прямоугольника.

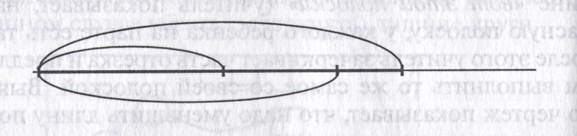
11.Учебник, ч. I.e. 24. Упр. 7. По рисунку устанавливается, что с водой в сосуде последовательно провели два дейст­вия, причем оба раза объем воды увеличивали. После того как дети изобразят это на чертеже, учитель предлагает показать на нем с помощью дуг разного цвета все три объема (исходный, получившийся после первого увели­чения, итоговый).

Дата добавления: 2014-11-16