Обозначение величин буквами

1. На столе у учителя стоит сосуд с водой, а на доске изоб­ражен чертеж:

Учитель сообщает, что в другом классе ученики изменили объем воды в сосуде и показали это на чертеже. Детям предла­гается угадать, какое действие сделали ученики другого класса, и выполнить его.

Выясняется, что по этому чертежу нельзя сказать, увеличи­вали объем или уменьшали. На нем выделены два объема, но не ясно, какой из них был сначала, а какой получился потом.

Учитель сообщает детям, что он знает, какое действие было совершено, и поможет им это узнать, но чтобы было интерес­нее, он покажет это с помощью значков. После этого учитель отмечает на чертеже выделенные объемы какими-нибудь знач­ками и делает запись, состоящую из этих значков, соединен­ных стрелкой:

Дети (при помощи учителя) выясняют, что первый значок в записи (галочка) обозначает больший объем, второй значок (крестик) обозначает меньший объем, а стрелка показывает, какой из объемов был сначала и какой получился потом. Уста­навливается, что запись говорит об уменьшении, так как сна­чала объем воды был больше, чем стал потом. Кто-нибудь из детей выходит к столу и отливает воду из сосуда.

Учитель сообщает, что в математике величины обычно обо­значают буквами, предлагает выбрать буквы и переделать за­пись. Чтобы показать произвольность выбора букв, на доске фиксируется несколько вариантов записи

А→Н С→Т

2. Учебник, ч. 2, с. 3. Упр. 1. По рисунку устанавливается, что объем воды увеличили. Обсуждая рисунок, дети вы­ясняют, что сначала был объем А, потом получился объ­ем П. Соответствующие буквы вставляются в чертеж (в учебнике и на доске).

Далее предлагается провести указкой по отрезку, обознача­ющему объем А, объем П. (Заметим, что такие показы нужно практиковать часто. Некоторые дети, работая с буквами и ду­гами, начинают считать изображением величины дугу или бук­ву, а не отрезок; например, при просьбе показать величину П они обводят дугу или указывают на букву.)

3.Учебник, ч. 2, с. 3. Упр. 2. Если в упр. 1 буквы были зада­ны, то теперь их нужно подобрать самим. Это должно быть сделано так, чтобы еще раз показать, что могут быть взяты любые буквы.

4.Учебник, ч. 2, с. 3. Упр. 3. По рисунку дети определяют, какая величина обозначена буквой (в обоих случаях ко­личество), и находят ее на чертеже. Далее определяется, какая еще величина показана на чертеже и какое дейст­вие надо совершить, чтобы получить ее из данной. Со­ответствующее действие совершается (на рисунке зачеркиваются лишние или добавляются новые фигу­ры), а под рисунком делается запись проделанного дей­ствия (к букве, обозначающей исходную величину, до­писываются стрелка и буква, обозначающая получен­ную величину).

К→Т А→Р

5. Учебник, ч. 2, с. 4. Упр. 4. Задание аналогично предыду­щему, только разные действия с разными величинами представлены одним чертежом.

6. Учебник, ч. 2, с. 4. Упр. 5, 6. В отличие от прежних за­даний, здесь производятся два изменения величины, а поэтому для обозначения всего процесса требуются три буквы.

7. Учебник, ч. 2, с. 5. Упр. 7. Буквы присваиваются величи­нам вне ситуации их изменения. Сначала выясняется, какая величина представлена отрезками и обозначена буквами.

Дети могут сказать, что А — это мышь. Следует уточнить, что это может быть высота животных, а может быть их масса. Лучше остановиться на массе. Предлагается вписать буквы под рисунками и правильно прочитать запись: масса А (а не мыш­ка А) и т. д.

8.Сохранение величин. Учитель показывает квадрат. Под­бирается буква для обозначения его площади (А). От ква­драта отрезается и откладывается уголок. Теперь пло­щадь фигуры должна быть обозначена другой буквой (С). Буквы записываются на доске: А→С

Учитель приставляет отрезанный уголок на прежнее место — опять получилась величина А, добавили столько же, сколько убавили. Запись дополняется новой стрелкой и бук­вой А: А→С→А

Учитель приставляет отрезанный уголок к иному месту на фигуре. Какова теперь площадь? У некоторых детей воз­никнет замешательство. Другие дети или учитель разъясняют, что площадь фигуры осталась той же, что была вначале (доба­вили столько же, сколько убавили), изменилась лишь ее фор­ма. Запись остается той же самой.

9. Учебник, ч. 2, с. 5. Упр. 8. Выясняется, что на рисунке показаны два последовательных изменения количе­ства: сначала количество звездочек уменьшается, а затем увеличивается. Однако оказывается, что добавили столько же звездочек (две красные), сколько убрали (две желтые), в результате получится то же количество звез­дочек, что и исходное (А), хотя сами группы звездочек различны. Равенство исходного и получившегося в ито­ге количеств проверяется: проводятся линии, соединяю­щие звездочки на первом рисунке со звездочками на третьем рисунке (одна к одной). Вводится только одна новая буква — для обозначения меньшего количества (средний рисунок), а на чертеже выделяется только один отрезок.

10. Уточнение представлений детей о площади. У детей и учителя квадрат. На доске записывается обозначение его площади (Т). Далее квадрат разрезается по диагонали (рис. а) и из полученных треугольников составляется но­вый треугольник (рис. б).

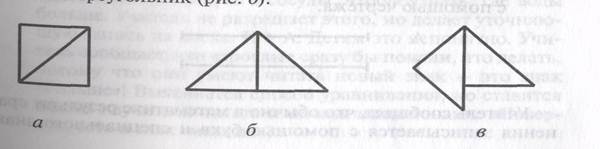
У. Как теперь нужно обозначить площадь фигуры?

Выясняется, что полученные треугольники вместе также составляют площадь Т, — ее разрезали, но ничего не отброси­ли и ничего не добавили, у новой фигуры такая же площадь, как и была, но другая форма.

Предлагается еще раз изменить форму фигуры (рис. в). Же­стом показывается ее площадь: она такая же, как и была (Т).

11. Учебник, ч. 2, с. 6. Упр. 9.

12. Учебник, ч. 2, с. 6, 7. Упр. 10 — 11. Работая с площадью и длиной, дети изменяют первоначально выбранную букву только при изменении величины, но не формы объектов.

13. Учебник, ч. 2, с. 7. Упр. 12—13. Если величины равны, то они обозначаются одной буквой и изображаются одним и тем же отрезком.

Дата добавления: 2014-11-16