Разность чисел

Разностное сравнение величин сложение и вычитание чисел (17 уроков)

Критерии усвоении учебного материала

Единицы счета

1. Повторяются известные детям единицы длины. Ставится задача выяснить, какие единицы люди договорились ис­пользовать для измерения количества.

У детей на партах 6 кругов и 4 квадрата. Это величина А. Нужно ее измерить и сообщить число. Если учащиеся спросят о мерке, предложить им придумать мерку самостоятельно. Скорее всего, дети пересчитают фигуры по одной и получат число 10. Предлагается назвать мерку, единицу счета. Можно ли сказать, что это 10 метров? 10 см? 10 квадратов? Дети могут сказать «10 фигур».

У. Покажите мерку... Теперь посчитайте фигуры вот такой меркой (показывается пара фигур).

Дети получают число 5. «Как назвать эту мерку? Нельзя же сказать, что здесь 5 фигур!»Предлагается обратиться к учебнику. Читаются названия единиц. Дети уточняют резуль­таты своих измерений: 10 штук и 5 пар

2.Учебник, ч. 2, с. 45, 46. Упр. 1 - 5. Выполняя задания, уча­щиеся переходят в счете от одной единицы к другой. В упр. 2 они должны догадаться о единице счета по задан­ному числу.

3.Учебник, ч. 2, с. 47. Упр. 6 — 8. Производится счет геоме­трических объектов. Выбирается самая простая едини­ца — штука, но поясняется, что часто слово «штука» заме­няют названием тех объектов, которые пересчитывают: 3 отрезка, а не 3 штуки, хотя второе не является ошибкой.

У. Как считали игрушки, если ответ получился 4 машинки?

Д. Считали штуками.

В упр. 7 важно увидеть на последнем рисунке 3 отрезка.

Учащиеся должны:

1) уметь сравнивать числа на числовой прямой, знать, что чем дальше число отстоит от начала, тем оно больше;

2) знать зависимость между величинами и числами при усло­вии использования одной и той же мерки;

3) понимать зависимость между мерками и числами при изме­рении одной и той же величины;

4) знать единицы длины и счета.

В этой теме уточняется отношение неравенства величин. Выявляется их разность — величина, характеризующая сте­пень различия между величинами. Это отношение моделиру­ется на числовой прямой, что позволяет ввести действия сло­жения и вычитания для чисел как присчет и отсчет шагов на числовой прямой. Рассматриваются выражения, описываю­щие эти действия. Вводится число 0.

Дети тренируются в мысленном движении по числовой прямой на 1, 2, 3 шага от заданного числа.

1.Демонстрируются два сосуда одинаковой формы и раз­мера, но с разным объемом воды в них. Выясняются и выполняются реально и на чертеже два способа уравни­вания объемов: увеличение меньшего до уровня больше­го и наоборот — уменьшение большего. По ходу работы учитель пытается долить или отлить «неправильный» объем воды. При обсуждении этих ошибок подчеркива­ется, что добавлять или отливать нужно не любую вели­чину, а определенную — разность, то, на сколько различа­ются объемы в обоих сосудах. Предлагается показать на сосудах эту разность как избыток в большем объеме и как недостаток в меньшем.

2. На столе учителя два сосуда разных размеров и с разным объемом воды в них, а на доске изображена числовая прямая. Устанавливается, что в первом сосуде объем во­ды меньше, чем во втором (сосуды такие и в них столько налито, что это сразу видно, см. рис.).

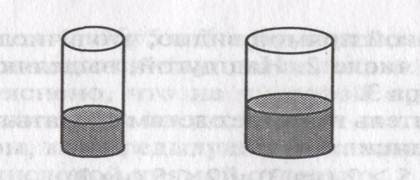
Учитель предлагает уравнять объемы воды в сосудах. Выби­рается любой из способов уравнивания, например, доливание воды в первый сосуд. Однако теперь нельзя ориентироваться на уровень воды в сосудах. «Как же определить объем воды, которую нужно долить в первый сосуд?»

Дети предлагают произвести измерение. Учитель дает мер­ку (стаканчик). Кто-то из детей промеривает воду в первом сосуде и результат (2 мерки) отмечает дугой на числовой пря­мой. После этого другой ученик измеряет объем воды во вто­ром сосуде и отмечает свой результат (5 мерок) на числовой прямой.

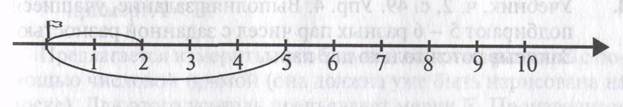
Учитель предлагает показать разность на чертеже. Дети вы-целяют ее дугой другого цвета.

У. Теперь вы можете уравнять объемы воды в сосудах?

Д. Да. Надо долить в первый сосуд три мерки.

Дети выполняют уравнивание. Для проверки вода из этих сосудов переливается в другие, одинаковые по форме и размеру

Еще раз уточняется, что по чертежу дети смогли опреде­лить, на сколько мерок во втором сосуде воды больше, на сколь­ко мерок в первом сосуде воды меньше (используется новый зля детей оборот речи).

Далее учитель показывает два прямоугольника и сообщает, по их площади измерили меркой К. Площадь первого оказалась 2К, а площадь второго — 5 К. Детям предлагается догадать­ся, на сколько площадь одного больше площади другого. Надо т для этого делать новый чертеж? Оказывается, можно и по старому чертежу определить разность. Она состоит из трех мерок К. На числовой прямой видно, что в числе 5 на 3 едини­цы больше, чем в числе 2. Над дугой, выделяющей разность, записывается цифра 3.

После этого учитель помогает детям сделать и прочитать со­ответствующие записи:

5 > 2 (на 3) и 2 < 5 (на 3).

2.Учебник, ч. 2, с. 48. Упр. 1, 2.

3.Учебник, ч. 2, с. 48. Упр. 3. На свитке изображена сказоч­ная числовая прямая. Хотя начала не видно, но стрелка позволяет определить, в какой оно стороне. Поэтому можно установить, какое число больше и на сколько. На­пример, число Q на один шаг дальше числа ╧, значит, оно на 1 больше.

4. Учебник, ч. 2, с. 49. Упр. 4. Выполняя задание, учащиеся подбирают 5 — 6 разных пар чисел с заданной разностью. Записываются только две пары.

5. Дети находят на числовой прямой указанное учителем число (6) и называют соседние числа. Сообщается, что число, находящееся на один шаг впереди, называют пре­дыдущим, а число, идущее следом, на один шаг даль­ше, — последующим. Выполняются упражнения 5 и 6 (учебник, ч. 2, с. 49). Подчеркивается, что разность со­седних чисел равна единице.

6.Предлагается дополнить сделанную на доске запись: 7... 9 (на _). Числа и разность показываются на числовой прямой жестом, записывается результат сравнения.

С помощью жестов сравнивается еще одна пара чисел — 9 и 7. Обнаруживается, что показано то же самое место на чис­ловой прямой.

С помощью числовой прямой выясняется разность чисел 5 и 8. Новое сравнение (8 и 5) уже не требует обращения к пря­мой: учащиеся говорят, что уже установили, что число 5 мень­ше числа 8 на 3, значит, число 8 больше числа 5 тоже на 3.

Разность чисел 9 и 6; 5 и 7 предлагается найти с помощью пальцев — «дети часто считают на пальцах». В результате проб должно быть уяснено, что на числовой прямой действовать проще. Обнаруживается также, что эти два задания не состав­ляют такой пары, как предыдущие, и каждое из них пришлось выполнять на числовой прямой отдельно.

7. Учебник, ч. 2, с. 49. Упр. 8. Нужно дополнить записи, не прибегая к числовой прямой и к пальцам. Учащиеся объ­ясняют, что первая запись позволяет дополнить вторую.

Дата добавления: 2014-11-16