Алгебраические дополнения и миноры

1º Минором некоторого элемента 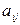определителя, называется определитель, получаемый из данного определителя путём вычёркивания строки и столбца, на пересечении которых расположен этот элемент и обозначается 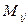. Например, минором элемента определителя = 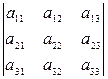является определитель 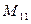= 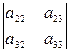, минором элемента является определитель 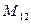= 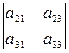и т.д..

2º Алгебраическое дополнение элемента 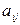равно минору этого элемента взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен этот элемент, есть число чётное, и с обратным, если это число – нечётное т.е. .

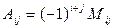3º Определитель равен сумме произведений элементов, какого-нибудь столбца (или строки) на их алгебраические дополнения. Например,

.

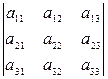
Пример 1. Вычислить определитель:

3. Решение системы методом Крамера. Исследование системы.

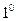Пусть дана система линейных уравнений с тремя неизвестными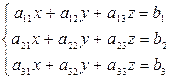

Решением системы называется совокупность чисел 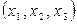, при подстановке которых все уравнения системы обращаются в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет решения.

Совместная система называется определенной, если она имеет только одно решение и неопределенной, если она имеет более одного решение.

Если все равны нулю, то система называется однородной.

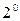Система трех линейных уравнений с тремя неизвестными

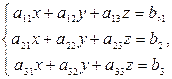
при условии, что определитель системы

=

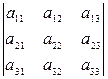
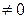
не равен нулю, имеет следующее единственное решение:

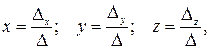(5)

где ; ; = .

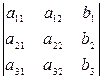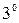Если определитель системы 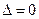, то возможны два предположения:

1. Элементы двух строк определителя пропорциональны, например: 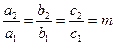, тогда:

а) если 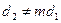,то система не совместна;

б) если 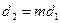, то система не определена;

2. Если найдутся числа 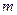и такие, что:

,

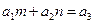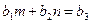
тогда: а) если 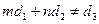, то система не совместна;

б) если 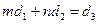, то система не определена.

Пример 2. Дана система линейных уравнений:

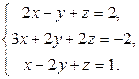
Установить, что система совместна и найти её решение методом Крамера.

Решение. Вычислим определитель системы методом разложения его по элементам строки. Разложим по первой строке:

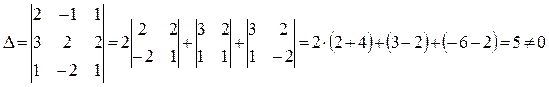
Так как определитель системы не равен нулю, система уравнений совместна и имеет единственное решение. Найдём решение системы по формуле Крамера.

; ;

; ;

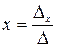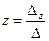
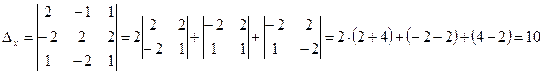
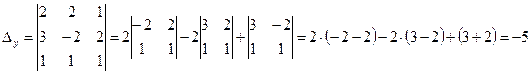
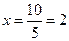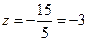
Пример 3. Решить систему уравнений.

Решение. 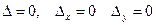и 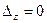. Однако система не имеет решений. В самом деле, умножим первое уравнение на -2 и сложим со вторым уравнением системы, получим 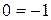, что не возможно, т.е. система не совместна и не имеет решений.

Пример 4. Решить систему уравнений:

Решение. 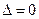, 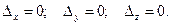Система имеет бесконечно много решений. В самом деле, складывая первые два уравнения, получаем третью и данная система имеет два существенных уравнения:

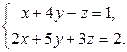
Следовательно, получим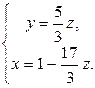

Контрольные вопросы

1. Определители.

2. Алгебраические дополнения и миноры.

3. Решение системы методом Крамера. Исследование системы.

Задания.

1. Вычислить определители, разложив их по элементам:а) первого столбца; б) по элементам третьей строки.

, .

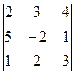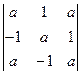2. Найти площадь треугольника с вершинами , , .

3. Вычислить миноры и алгебраические дополнения элементов второй строки определителя.

.

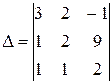4. Решить системы уравнений методом Крамера.

, , .

.

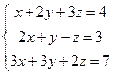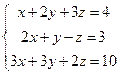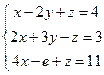Дата добавления: 2014-12-16