Занятие1

Элементы линейной алгебры и аналитической геометрии.

Математический анализ

4), 5), 6).

Типовой расчёт по теме «Предел и производная»

Задача 1. Вычислить

№			№

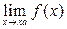
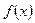
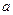
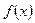
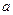
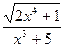
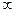
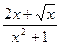
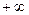
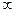
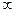
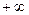
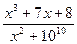
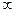
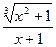
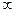
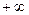
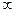
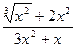
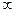
Задача 2. Вычислить 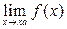, используя второй замечательный предел.

№			№

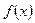
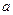
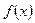
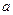
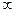
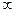
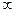
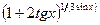
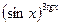
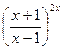
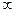
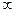
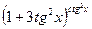
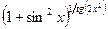
Задача 3. Вычислить 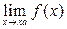с помощью замены бесконечно малых на эквивалентные.

№		№

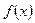
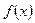
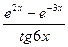
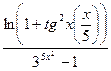
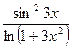
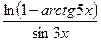
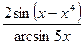
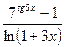
Задача 4. Найти точки разрыва функции .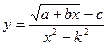

Определить характер разрывов.

№	а	b	с	k	№	а	b	с	k
							-1
							-2
		-2
		-1					-1

Задача 5. Найти производную функцию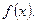

№		№

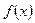
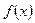
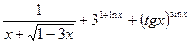
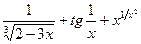
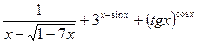
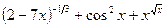
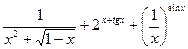
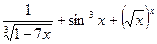
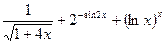
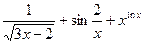
Задача 6. Найти производную функции, заданной

параметрически: .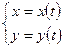

№			№

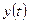
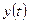
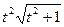
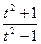
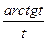
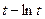
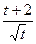
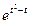
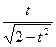
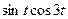
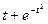
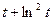
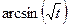
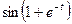
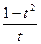
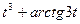
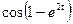
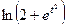
Задача 7. Найти производную неявной функции, заданной уравнением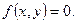

№		№

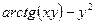
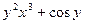
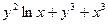
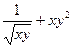
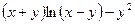
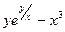
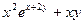
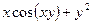
Задача 8. Вычислить с помощью дифференциала приближенное значение числа .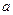

№

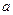
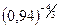
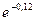
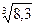
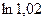
Задача 9. Определить, в каких точках заданной линии L касательная к этой линии параллельна прямой , и написать уравнение этой касательной.

№	Уравнение линии		№	Уравнение линии
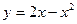
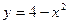
					-2
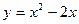
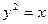
		-1
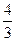
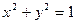
		-1
		-1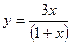

1. Координаты на прямой. Деление отрезка в данном отношении.

Прямая с выбранным на ней положительным направлением, началом отсчёта и единицей масштаба называется координатной осью.

1º Расстояние d между точкам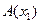и и 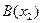на оси:

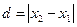(1)

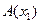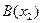2º Деление отрезка в данном отношении: даны точки и . Координата точки 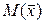, делящий отрезок 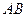в отношении , определяется по формуле:

(2)

В частности при делении отрезка пополам, т.е. в отношении имеем

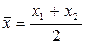(3)

Пример 1. Отрезок 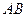двумя точками разделён на три равные части. Определить координаты точек деления, если ,

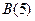
Решение. Пусть 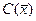ближайшая к точка деления, тогда 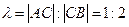= 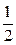Следовательно, по формуле (2) находим:

т.е. .

Пусть теперь точка деления ближайшая к , тогда

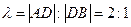=2

и по формуле (2) находим:

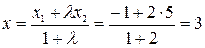
т.е.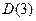

Ответ: , .

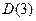2. Прямоугольная система координат на плоскости.

Две взаимно перпендикулярные оси Ох и Оy, имеющие общее начало отсчета О и одинаковую единицу масштаба образуют прямоугольную декартову систему координат на плоскости.

1º Расстояние между точками и на плоскости: 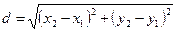. (4)

2º Деление отрезка в данном отношении: координаты точки 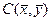, делящей отрезок между точками и в заданном отношении определяются по формулам:

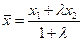; (5)

в частности, при делении отрезка пополам, т.е.

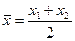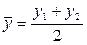; (6)

Пример 2. Определите расстояние между точкам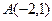и и .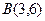

Решение. Воспользуемся формулой (4), получим:

.

Пример 3. Даны вершины треугольника: 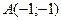, 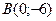и 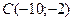. Найти длину медианы, проведённой из вершины .

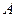Решение. Найдём координаты точки 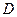- середины отрезка ; имеем:

; ; .

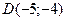Вычислим теперь длину медианы :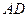

.

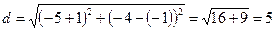Дата добавления: 2014-12-16