
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Полярные координаты
|
|
|
|
В полярной системе координат положение точки 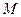 на плоскости определяется её расстоянием
на плоскости определяется её расстоянием  от полюса
от полюса  (
(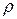 -полярный радиус вектор точки M) и углом
-полярный радиус вектор точки M) и углом 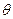 , образованный отрезком
, образованный отрезком  с полярной осью Ох (
с полярной осью Ох ( полярный угол точки). Угол
полярный угол точки). Угол 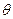 считается положительным при отсчёте от полярной оси против часовой стрелки.
считается положительным при отсчёте от полярной оси против часовой стрелки.
Если начало декартовой системы координат совместить с полюсом, а ось  направить по полярной оси, то прямоугольные координаты
направить по полярной оси, то прямоугольные координаты  и
и  точки
точки 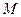 и её полярные координаты
и её полярные координаты 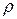 и
и 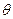 связаны формулами:
связаны формулами:
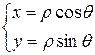 (7)
(7)


Пример 4. Найти прямоугольные координаты точки 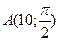 , если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.
, если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.
Решение. Используя формулу (7) имеем:
 ,
,  .
.
Итак, 
4. Прямоугольная система координат в пространстве.
Три взаимно перпендикулярные координатные оси Ох, Оу, Оz с общим началом О и одинаковой единицей масштаба образуют прямоугольную декартову систему координат в 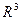 .
.
Точка О - начало координат, Ох - ось абсцисс, Оу - ось ординат,  Оz - ось аппликат.
Оz - ось аппликат.
Пусть М произвольная точка пространства и  - радиус вектор точки М. Проекции радиус вектора
- радиус вектор точки М. Проекции радиус вектора  на оси координат
на оси координат  ,
, 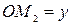 ,
,  называются прямоугольными координатами точки
называются прямоугольными координатами точки  или вектора
или вектора 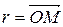 . Таким образом, в выбранной системе координат каждой точке
. Таким образом, в выбранной системе координат каждой точке  соответствует единственная упорядоченная тройка
соответствует единственная упорядоченная тройка 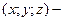 её прямоугольные координаты и обратно, каждой упорядоченной тройка
её прямоугольные координаты и обратно, каждой упорядоченной тройка 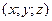 соответствует, и притом одна единственная точка
соответствует, и притом одна единственная точка  в пространстве
в пространстве 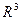 .
.
1º Расстояние  между точками
между точками  и
и 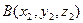 :
:
 (8)
(8) 
В частности, расстояние точки 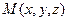 от начала координаты определяется:
от начала координаты определяется:
 (9)
(9)
2º Если отрезок, концами которого служат точки  и
и 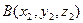 разделён точкой
разделён точкой  в отношении
в отношении  , то координаты точки
, то координаты точки  определяются соотношением:
определяются соотношением:
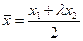 ;
;  ;
; 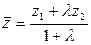 . (10)
. (10)
Пример 5. Даны точки  и
и 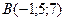 . Найти координаты точек
. Найти координаты точек  и
и 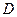 , делящих отрезок
, делящих отрезок 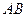 на три равных части.
на три равных части.
Решение. Пусть  ближайшая к
ближайшая к 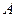 точка деления, тогда
точка деления, тогда  =
= 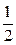 . Следовательно, по формуле (10) находим:
. Следовательно, по формуле (10) находим:

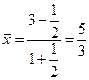 ;
;  ;
; 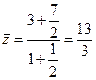 ;
;
т.е.  .
.
Пусть теперь 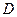 точка деления ближайшая к
точка деления ближайшая к  , тогда
, тогда 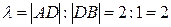 и по формуле (10) находим:
и по формуле (10) находим:
 ;
;  ;
; 
т.е.  . Ответ:
. Ответ:  ,
,  .
.
Контрольные вопросы
1. Координаты на прямой. Деление отрезка в данном отношении.
2. Прямоугольная система координат плоскости.
3. Полярные координаты.
4. Прямоугольная система координат в 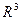 .
.
Задания.
1) Определить расстояние между точками: а) 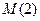 и
и  ; б)
; б) 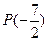 и
и  .
.
2) Найти точку 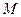 , симметричную точке
, симметричную точке 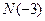 относительно точки
относительно точки 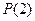 .
.
3) Найти координаты середины отрезка, если известны его концы: 1)  и
и  ; 2)
; 2) 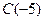 ,
, 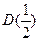 .
.
4)Определить расстояние между точками: 1)  и
и 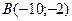 ; 2)
; 2)  и
и  .
.
5) Известны точки  ,
,  - концы отрезка
- концы отрезка 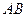 . Показать, что на этом отрезке находится точка
. Показать, что на этом отрезке находится точка  , расстояние которой от точки
, расстояние которой от точки 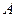 в два раза больше расстояния от точки
в два раза больше расстояния от точки  .
.
6) Построить точки, заданные полярными координатами 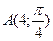 ,
,  ,
,  ,
, 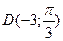 .
.
7) Определить расстояние между точками 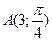 и
и  . (Применить к треугольнику
. (Применить к треугольнику 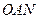 теорему косинусов.)
теорему косинусов.)
9) Найти полярные координаты точек, симметричных точкам 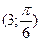 ,
,  ,
,  : 1) относительно полюса; 2) относительно полярной оси.
: 1) относительно полюса; 2) относительно полярной оси.
10) Найти координаты центра тяжести треугольника с вершинами  ,
,  и
и 
11) В каком отношении точка 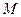 равноудалённая от точек
равноудалённая от точек  и
и 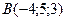 , разделит отрезок от начала координат до точки
, разделит отрезок от начала координат до точки 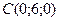
12) Даны следующие вершины куба 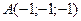 ,
,  ,
, 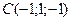 и
и  . Определить его остальные вершины.
. Определить его остальные вершины.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 825; Нарушение авторских прав?; Мы поможем в написании вашей работы!