Системы уравнений

ТЕМА 3. ЛИНЕЙНАЯ АЛГЕБРА

Задачи для самостоятельного решения

Пример 3.

Пример 2.

Какую линию определяет уравнение x2+4x-8y+12=0.

Решение.

Преобразуем данное уравнение следующим образом:

(x ²+4 x +4)-4=8 y -12

(x +2)²=8 y -12+4

(x +2)²=8(y -1) – парабола.

Установить вид кривой 4 x ²- y ²-4 y -8 x =12.

Решение.

Используем свойства пятичленного уравнения кривой второго порядка:

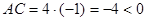- гипербола.

Задание 1.

Соответствие между уравнениями парабол и координатами их вершин:

(4, -2)	y^2- 4x + 4y + 20 = 0
(-2, 4)	x^2+ 4x - 4y + 20 = 0
(-2. -2)	y^2+ 4x + 4y + 12 = 0
(-2, -4)	x^2+ 4x + 4y + 20 = 0

Задание 2.

В порядке увеличения радиусов окружности располагаются:

1: x² + y² + 2y + 2x = 2

2: x² + y² + 2y - 4x = 1

3: x² + y² + 4y - 2x = 5

Задание 3.

Соответствие уравнения парабол и координат их вершин

(1, -2)	y^2- 8x + 4y + 12 = 0
(- 4, 2)	x^2+ 8x - 4y + 24 = 0
(- 2, -2)	y^2+ 4x + 4y + 12 = 0
(-1, -2)	x^2+ 2x + 4y + 9 = 0

Задание 4.

Порядок расположения окружностей по увеличению их радиусов

1: x² + y² - 2y = 2

2: x² + y² - 4y - 2x = 3

3: x² + y² + 2y + 2x = 2

Задание 5.

Соответствие уравнений и графиков

парабола	x^2+ 4x - 8y + 12 = 0
окружность	4x^2+ 4y^2- 7y - 9x -16 = 0
эллипс	4x^2+ 9y^2+ 18y - 16x - 11 = 0
гипербола	4x^2- y^2- 4y - 8x = 12

Задание 6.

Кривая x² – y² –4x +6y = 9 имеет центр в точке с координатами…

R (2, 3)

£ (4, 9)

£ (4, 6)

£ (4, -6)

£ (2, -3)

£ (-2, 3)

Задание 7.

Ветви параболы y² – 4y + 2x + 8 = 0 направлены…

R влево

£ вправо

£ вниз

£ вверх

Задание 8.

Уравнение 4x² – 5y² +20x +30y + 10 = 0 определяет…

R гиперболу

£ параболу

£ окружность

£ эллипс

Пусть дана система n линейных уравнений с n неизвестными;

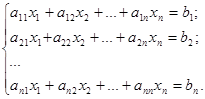(3.1)

Здесь a_ik – коэффициенты системы, b₁, b₂, …, b_n – свободные члены. Если все свободные члены равны нулю, то система называется однородной.

Матрица 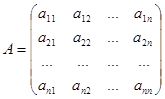называется матрицей системы (3.1), а ее определитель |А| является определителем исходной системы уравнений (3.1). Решением системы называется совокупность чисел x _i= л _i (i =1, 2, …, n), обращающих все уравнения системы в тождества. Если система линейных уравнений не имеет решений, то она называется несовместной. Если она имеет хотя бы одно решение, то она называется совместной.

Запишем матрицу-столбец Х из неизвестных и матрицу-столбец В их свободных членов так:

; .

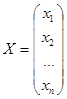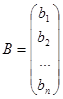Тогда исходную систему уравнений можно записать следующим образом: АХ=В (считается, что определитель исходной системы (3.1)не равен нулю). Эта запись является матричным уравнением.

Введем обозначения: пусть ∆ - определитель системы линейных уравнений (3.1), ∆ ⁱ – определитель, полученный из определителя ∆ заменой его i -го столбца столбцом свободных членов. Тогда имеет место теорема Крамера (формулы Крамера) о решении системы (3.1): если определитель системы линейных уравнений не равен нулю, то эта система имеет единственное решение 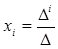, где i =1, 2, …, n.

Дата добавления: 2014-12-17