Приклад 6. 2

Припустімо, що ви зробили депозитний внесок у банк у сумі 1 000 грн терміном на три роки з нарахуванням відсотків наприкінці року за ставкою 10%.

Для визначення суми внеску з використанням обох методів ~ простого і склад­ного відсотків — здійснімо відповідні розрахунки (табл. 6.1).

Таблиця 6.1. Зіставлення методики розрахунку простих і складних відсотків

У разі довготермінових інвестицій переважно використовують складні від­сотки, які дають більший дохід, ніж прості.

J Майбутня вартість (Future Value) — це вартість інвестицій через визначений період часу з ураху­ванням певної ставки відсотка.

У нашому прикладі майбутню вартість інвестицій у сумі 1 000 дол. за склад­ного відсотка і = 10% та п = З було розраховано так:

(1 000 + 1 000 • 0 + [(1 000 + 1 000 • і) • /] + [(1 000 + 1 000 • /) + (1 000 + 1 000 • 0 • /] ■ і = = 1 000 [(1 + 0 + (/ + Р) + (і + Р) + (Р + Р)] = 1 000 [(1 + 3/ + ЗР + Р)] = = 1 000 [(1 + /)(1 + /)(1 + 0] = 1 000 (1 + О³ = 1 000 (1 + ОД)³ = 1 331.

Звідси випливає, що для обчислення майбутньої вартості інвестицій можна скористатися формулою:

FV = PV (1 + 0" (6.1)

де FV — майбутня вартість; PV — теперішня вартість; і — ставка складного відсотка; п — кількість періодів нарахування відсотків. З наведеної формули бачимо, що майбутня вартість одної грошової одиниці

дорівнює (1 + і)^п.

Для спрощення розрахунків майбутньої вартості можна користуватися таб­лицею складних відсотків (додаток 1.1), що містить готові розрахунки за форму­лою (1 + і)" для різних значень (/) та (п).

Використовуючи цю таблицю, побачимо, що на перехресті значень і = 10% та п = 3 майбутня вартість 1 грн (або іншої грошової одиниці) дорівнює 1,331.

Отже, майбутня вартість 1 000 грн дорівнює: 1 000 • 1,331 = 1 331 грн.

J Теперішня вартість (Present Value) — це вартість майбутніх грошових потоків на теперішній час.

Для визначення теперішньої вартості інвестицій необхідно з суми майбутніх грошових надходжень вирахувати суму відсотків, нарахованих за певною ставкою (/) за певний період (п).

Процес коригування майбутніх грошових надходжень для визначення тепе­рішньої вартості їх називають дисконтуванням.

Дисконтування (Discounting) — процес визначення теперішньої вартості май­бутніх грошових потоків.

Відповідно, ставку відсотка, що використовують для дисконтування, назива­ють Ставкою дисконту (Discount Rate).

Теперішню вартість інвестицій мона обчислити за формулою:

У цьому разі ставку відсотка (/'), використану для дисконтування, називають ставкою дисконту.

Відповідно, теперішня вартість однієї грошової одиниці дорівнює: 1: (1 + і)^п або (1 + ifⁿ і також може бути визначена за спеціальною таблицею (додаток 1.2). Так, у цій таблиці на перетині значень і = 10% та п = 3 маємо показник 0,75132. Виходячи з цього, теперішня вартість суми 1 331 грн дорівнює:

1 331 -0,75132= 1 000 грн. Аналогічний результат отримаємо за формулою:

1 331: (1 + 0,1)³ = 1 331: 1,331 = 1 000 грн.

Взаємозв'язок між теперішньою та майбутньою вартістю можна проілюстру­вати графічно (рис. 6.4).

Ануїтет і Ануїтет (Annuity) -це ———^J серія рівновеликих платежів (або надходжень), що здійснюються через однакові проміжки часу впродовж певно­го періоду.

Якщо момент оцінювання ануїтету передує моментові пер­шої виплати або збігається з ним, тоді дисконтована величина ануї­тету є його теперішньої вартістю.

Відповідно, майбутня вар­тість ануїтету (Future Value of Annuity) — це вартість ануїтету на момент останньої виплати.

Припустімо, що за три роки щорічний внесок (наприкінці ро­ку) в банк на депозитний раху­нок становив 1 000 дол., а відсоток нараховували за ставкою 10% річних.

Графічно точки часу, в яких визначається теперішня і майбутня вартість ви­плат, можна показати так:

1 000 1 000! ⁰⁰° PV ■-----------------------------•------------------------.--------------------------• FV

Для визначення майбутньої вартості ануїтету необхідно розрахувати майбут­ню вартість кожної виплати і підсумувати отримані результати.

У нашому прикладі майбутня вартість ануїтету:

FVA= 1 000-(1 + 0,1)² + 1 000-(1 + 0,1)' + 1 000 - (1 + 0,1)" =

= 1 000-1,21 + 1 000- 1,1 + 1 000- 1 = 1 210 + 1 100 + 1 000 = $3 310.

Майбутню вартість ануїтету (FVA) можна розрахувати за формулою:

FVA = А х ((1 + і)«- 1) _: і (6.3)

Майбутня вартість ануїтету за одним договором відповідно дорівнюватиме ((1 + і)" — 1): / й може бути визначена за таблицею відсоткового чинника майбут­ньої вартості ануїтету (FVIFA), наведеною в додатку 1.3.

У цій таблиці на перетині значень і = 10% та п = 3 маємо чинник майбутньої вартості ануїтету, який дорівнює 3,31.*

Отже, FVA = 1 000 • 3,31 = $3 310.

Теперішня вартість ануїтету (Present Value of Annuity) — це дисконтована сума ануїтету на дату останньої виплати.

Для визначення теперішньої вартості ануїтету (PVA) необхідно обчислити теперішню вартість кожної виплати і підсумувати отримані результати.

Припустімо, що нам треба визначити теперішню вартість ануїтету, виходячи з умов розглянутого раніше прикладу (А = 1 000, і = 10%, п = 3).

У цьому разі

PVA = 1 000: (1 + ОД)¹ + 1 000: (1 + ОД)² + 1000: (1 + ОД)³ =

= 1 000: 1,1 + 1 000: 1,21 + 1 000: 1,331 = 909,1 + 826,4 + 751,3 = 2 486,8 = $2 487.

Для визначення теперішньої вартості ануїтету можна використати формулу: PVA = А• ((1 - (1 + і)^п): і (6.4)

Для спрощення розрахунку значень ((1 — (1 + /)■"): і можна знайти в таблиці відсоткового чинника теперішньої вартості ануїтету (PVIFA), наведе­ної у додатку 1.4.

Необхідність дисконтування при оцінюванні інвестиційних проектів зумов­лена тим, що, розглядаючи проекти капітальних інвестицій, слід зіставити їх ви­годи з іншими ймовірними проектами. Визначивши теперішню вартість проекту з високим ризиком, ми можемо зіставити її із сумою, котру треба вкласти в надійні цінні папери, щоб за того самого відсотка і за той самий період отримати ту саму суму грошових надходжень, але з меншим ризиком.

Таке зіставлення дає змогу визначити, чи виправданий ризик і чи варто прий­мати той чи інший проект. Однак виникає питання: яку відсоткову ставку (став­ку дисконту) використати для визначення теперішньої вартості проекту капіталь­них інвестицій.

Ставкою дисконту, зокрема, може бути:

/ кредитна ставка банку;

/ середньозважена вартість капіталу;

/ альтернативна вартість капіталу;

/ внутрішня норма прибутковості.

Ставка дисконту, що використовується для визначення теперішньої вартості майбутніх грошових надходжень при оцінюванні проектів капітальних інвестицій, здебільшого базується на вартості капіталу компанії.

Вартість капіталу (Cost of Capital) — це комбінований (середньозважений) відсоток прибутку, що його компанія має сплачувати своїм інвесторам.

Для здійснення господарської діяльності підприємство залучає кошти з різ­них джерел і повинне заохочувати наявних і потенційних інвесторів.

Основними джерелами фінансування корпорації є надходження від випуску акцій, а також довготермінова кредиторська заборгованість.

Припустімо, що капітал компанії "Оптиміст" має таку структуру (табл. 6.2):

Виходячи з наведених даних, розрахуємо вартість власного капіталу, сфор­мованого завдяки випуску простих акцій:

Дивіденд на акцію: Ринкова вартість акції = 6: 40 = 0,15= 15% Аналогічно розраховують вартість привілейованих акцій:

10: 100 = 0,10 = 10%

Для розрахунку вартості облігацій припустімо, що ринкова вартість їх збіга­ється з номінальною, а податок на прибуток становить 30%.

На підставі цих припущень визначимо вартість довготермінового позикового капіталу:

0,1 -(1 -0,3) = 0,1-0,7 = 7%

Отримані результати дають змогу розрахувати середньозважену вартість капі­талу товариства "Оптиміст" (табл. 6.3).

Середньозважена вартість капіталу компанії "Оптиміст" дорівнює 12% і цю величину можна використати як ставку дисконту для визначення теперішньої вар­тості майбутніх грошових надходжень при оцінюванні інвестиційних проектів.

Доволі часто ставка дисконту, що використовується для оцінювання проек­тів капітальних інвестицій, вища за вартість капіталу підприємства.

По-перше, як уже згадувалося, поряд з проектами капітальних інвестицій, що дають пряму економічну вигоду, підприємства здійснюють проекти, спрямо­вані на поліпшення умов праці і мають лише соціальний ефект.

У зв'язку з цим ставка дисконту для прибуткових проектів має враховувати не тільки вартість капіталу компанії, а й вартість капітальних інвестицій, ефект яких не відображається у вигляді прибутку чи економії витрат.

По-друге, різні проекти капітальних інвестицій мають різну міру невизначе­ності й ризику.

Тож зрозуміло, що до різних проектів можуть бути застосовані різні ставки дисконту, які враховують цей ризик.

6.2. МЕТОДИ ОЦІНЮВАННЯ ПРОЕКТІВ КАПІТАЛЬНИХ ІНВЕСТИЦІЙ

Як уже згадувалося, всі методи оцінювання проектів капітальних інвестицій можна поділити на дві групи.

Найпоширенішими методами оцінювання, що передбачають дисконтуван­ня грошових потоків, є: чиста теперішня вартість та внутрішня норма прибут­ковості.

Чиста теперішня вартість (Net Present Value) — це різ­ниця між теперішньою вартістю майбутніх чистих гро­шових надходжень і теперішньою вартістю чистих інвес­тицій.

де С_п — чисті грошові надходження n-го періоду;

І — чисті інвестиції.

Для визначення чистої теперішньої вартості (ЧТВ) проекту капітальних ін­вестицій майбутні грошові надходження дисконтуються за допомогою відповід­ної ставки дисконту.

Потім із суми розрахованої таким чином теперішньої вартості майбутніх грошо­вих надходжень вираховують теперішню вартість чистих початкових інвестицій.

Якщо отримана в такий спосіб чиста теперішня вартість проекту більша або дорівнює нулю, це означає, що даний проект забезпечує компанії та її інвесторам необхідний прибуток, тому його можна прийняти.

Якщо ЧТВ має негативне значення, то, відповідно, цей проект не слід прий­мати, бо він не забезпечує мінімально необхідної прибутковості інвестицій.

Схематично алгоритм обчислення й інтерпретацію чистої теперішньої вар­тості проекту показано нарис. 6.5.

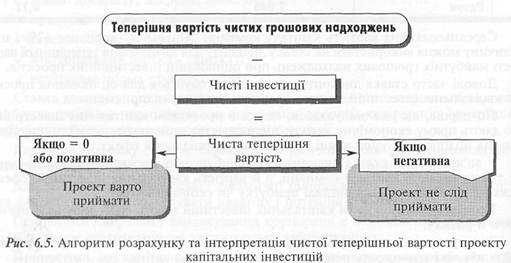
Для ілюстрації розрахунку чистої теперішньої вартості розглянемо такий приклад.

Дата добавления: 2014-11-29