Понятие модуля и аргумента комплексного числа

Лекция 43. ТРИГОНОМЕТРИЧЕСКАЯ И ПОКАЗАТЕЛЬНАЯ ФОРМЫ КОМПЛЕКСНОГО ЧИСЛА.

План:

1. Понятие модуля и аргумента комплексного числа.

2. Тригонометрическая форма комплексного числа.

3. Действия над комплексными числами в тригонометрической форме

4. Показательная форма комплексного числа.

5. Действия над комплексными числами в показательной форме.

Пусть комплексное число 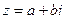изображено в виде вектора 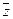с началом в точке О (0; 0) и концом в точке Z(a; b) (рис. 43.1). Любой вектор характеризуется двумя параметрами: длиной и направлением.

Модулем комплексного числа 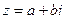называется длина соответствующего ему вектора.

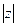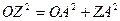
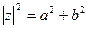
Модуль комплексного числа обозначается или r. Выведем формулу для его нахождения. Рассмотрим прямоугольный треугольник ОАZ (рис. 43.1). Очевидно, что ОА = а, ZА = b. Тогда длину гипотенузы ОZ легко найти по теореме Пифагора: r = 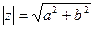(r > 0).

Аргументом комплексного числа 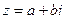называется угол φ, который образует вектор 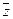с положительным направлением оси Ох.

Дата добавления: 2014-12-27