Проекцией вектора на координатную ось называется взятая с соответствующим знаком длина отрезка оси, заключённого между проекциями начала и конца вектора

Для равновесия системы сил, линии действия которых расположены в одной плоскости, необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух взаимно перпендикулярных осей, лежащих в плоскости действия сил, равнялась нулю и сумма моментов всех сил относительно оси, перпендикулярной плоскости действия сил, равнялась нулю

Плоскости

Условия равновесия системы сил, линии действия которых расположены в одной

Общий подход к решению задачи об определении реакций опор

РАВНОВЕСИЕ ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1

Во многих случаях, встречающихся в инженерной практике, заранее известно, что некоторое тело находится в равновесии. Например, оно соответствующим образом закреплено (имеет опоры). На тело действуют заданные силы, которые называют активными. Природа активных сил, как правило, не указывается, т.е. неважно какие тела и по каким физическим законам взаимодействуют с рассматриваемым телом, дан только результат этого взаимодействия в виде сил. Под действием активной нагрузки тело оказывает давление на опоры (связи), со стороны которых, в соответствии с третьим законом Ньютона, возникают реакции связей. Задача состоит в определении сил реакций связей.

Сила реакции связи заранее неизвестна, она зависит от приложенных к телу активных сил и вида самой связи. Заранее можно только утверждать, что сила реакции связи направлена в сторону, противоположную той, куда данная связь не даёт перемещаться телу.

При решении задач об определении сил реакций опор предлагается следующая последовательность действий.

1. Проведя сечение по соответствующим связям, выбрать тело (или систему тел), равновесие которого будет рассматриваться и изобразить на чертеже приложенную к выбранному телу активную нагрузку.

2. Ввести реакции связей, изобразив силы реакций на чертеже. Если направление сил реакций заранее неизвестно, необходимо показать их составляющие.

3. Составить условия равновесия для системы сил, приложенной к рассматриваемому телу и определить неизвестные. Эта система сил состоит из всех активных сил и всех реакций внешних связей.

4. Из составленных уравнений определить неизвестные величины.

В дальнейшем на лекциях будет показано, что

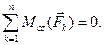(1.1)

где 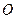– произвольно выбранная точка плоскости .

В курсе статики используется, в основном, декартова система координат, три взаимно перпендикулярных оси которой – 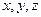, имеют орты .

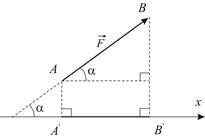
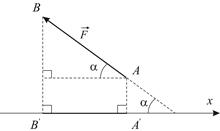
Первые два уравнения равновесия (1.1) связывают проекции векторов сил на выбранные координатные оси. Чтобы построить такую проекцию, нужно перенести ось параллельно самой себе так, чтобы она проходила через точку приложения силы и опустить перпендикуляры на ось из начала и конца вектора (Рис. 1.1-1.2):

Рис. 1.1		Рис. 1.2

Таким образом, ортогональная проекция вектора силы 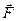на ось 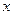определяется по формуле

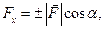
где – модуль силы; 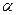– острый угол между двумя прямыми: линией действия вектора 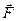и осью .

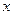При этом проекция положительна, если условное перемещение от проекции начала вектора 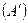к проекции его конца 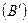совпадает с положительным направлением оси 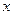и отрицательна в противоположном случае.

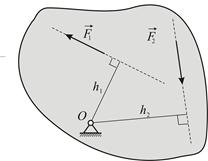
Третье уравнение (1.1) связывает так называемые моменты сил. Рассмотрим некоторую пластину, которая может вращаться вокруг оси 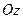, проходящей через закреплённую точку перпендикулярно плоскости пластины (Рис. 1.3). К пластине приложены две силы,

 

Рис. 1.3

которые стремятся вращать пластину в противоположные стороны. Куда будет вращаться пластина? Опыт показывает, что вращательный эффект силы зависит не только от её величины, но и от её расположения по отношению к оси. Вращательный эффект силы характеризует её момент относительно оси :

где – плечо силы, равное кратчайшему расстоянию от точки 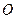до линии действия силы; знак «+» соответствует повороту вокруг точки 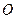против хода часовой стрелки.

Напомним, что мы говорим о силах, линии действия которых расположены в плоскости, перпендикулярной оси 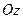. В дальнейшем будут введены общие понятия момента силы относительно точки и оси.

Дата добавления: 2014-12-25