
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 1.6
|
|
|
|
Пример 1.5
Определить реакции опор 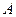 и
и 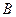 балки, находящейся под действием двух сосредоточенных сил и равномерно распределённой нагрузки. Дано:
балки, находящейся под действием двух сосредоточенных сил и равномерно распределённой нагрузки. Дано: 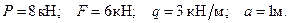

|
| Рис. 1.32 |
Найдём равнодействующую распределённой нагрузки. Модуль равнодействующей равен

плечо силы  относительно точки
относительно точки 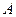 равно
равно  Рассмотрим равновесие балки. Силовая схема представлена на Рис. 1.33.
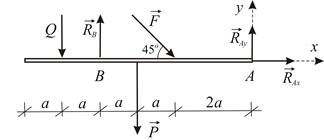
Рассмотрим равновесие балки. Силовая схема представлена на Рис. 1.33.
|
| Рис. 1.33 |
Условия равновесия в рассматриваемом случае имеют вид:



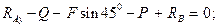
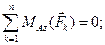
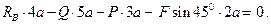
Определить реакцию заделки консольной балки, находящейся под действием сосредоточенной силы, пары сил и распределённой нагрузки (Рис. 1.34).
Дано: 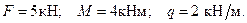
Заменим распределённую нагрузку тремя сосредоточенными силами. Для этого разобъём эпюру распределённой нагрузки на два треугольника и прямоугольник. Находим

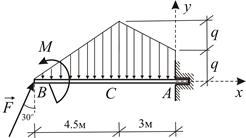
Силовая схема представлена на Рис. 1.35.
| 
| |
| Рис. 1.34 | Рис. 1.35 |
Вычислим плечи равнодействующих относительно оси 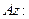
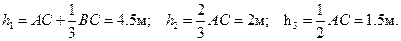
Условия равновесия в рассматриваемом случае имеют вид:

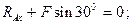

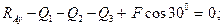
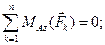
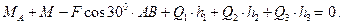
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
1. Что называется интенсивностью распределённой нагрузки?
2. Как вычислить модуль равнодействующей распределённой нагрузки?
3. Как вычислить координату точки приложения равнодействующей распределённой
нагрузки?
4. Чему равен модуль и какова координата точки приложения равномерно распределённой нагрузки?
5. Чему равен модуль и какова координата точки приложения линейно распределённой нагрузки?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 4.28; 4.29; 4.30; 4.33; 4.34.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-2; СР-3.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 529; Нарушение авторских прав?; Мы поможем в написании вашей работы!