
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Равновесие составных тел
|
|
|
|
СТАТИЧЕСКИЙ РАСЧЁТ КУНСТРУКЦИЙ
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5
При решении задач об определении опорных реакций может оказаться, что из составленных условий равновесия невозможно определить все неизвестные величины, так как их число больше числа уравнений, в которые эти неизвестные входят. Подобное может произойти по двум основным причинам.
Во-первых, на рассматриваемое тело могут быть наложены лишние связи, ненужные для обеспечения равновесия абсолютно твёрдого тела, но необходимые для предотвращения недопустимо больших деформаций. В этом случае задача определения реакций опор является статически неопределимой в том смысле, что невозможно определить реакции связей без учёта деформаций тела, т.е. оставаясь в рамках модели абсолютно твёрдого тела. Такие задачи в теоретической механике не рассматриваются.
Во-вторых, в качестве тела, равновесие которого рассматривается, может быть выбрана конструкция, состоящая из двух или более тел, соединённых между собой внутренними связями. На такую конструкцию заведомо приходится накладывать дополнительные связи, обеспечивающие равновесие конструкции. Основная особенность решения таких задач состоит в том, что необходимо рассматривать равновесие нескольких тел данной конструкции.
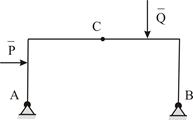
Рассмотрим, например, трёх шарнирную арку 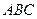 , нагруженную активными силами
, нагруженную активными силами 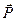 и
и  (Рис. 2.1). Можно рассмотреть равновесие арки в целом. Тогда в систему внешних сил войдут заданные силы
(Рис. 2.1). Можно рассмотреть равновесие арки в целом. Тогда в систему внешних сил войдут заданные силы 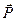 и
и  и силы реакций внешних опор – шарниров
и силы реакций внешних опор – шарниров 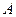 и
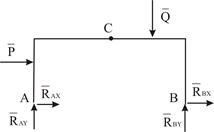
и  . Соответствующая силовая схема представлена на Рис. 2.2.
. Соответствующая силовая схема представлена на Рис. 2.2.
| 
| |
| Рис. 2.1 | Рис. 2.2 |
Хотя такая арка не является абсолютно твёрдым телом, заранее известно, что она покоится и, следовательно, приложенные к ней силы удовлетворяют условиям равновесия. Наличие шарнира  позволяет двум частям арки поворачиваться друг относительно друга. Для предотвращения такого поворота приходится усиливать одну из опор, например, ставить в точке
позволяет двум частям арки поворачиваться друг относительно друга. Для предотвращения такого поворота приходится усиливать одну из опор, например, ставить в точке  шарнирно неподвижную опору вместо шарнирно подвижной. При этом число неизвестных составляющих сил реакций увеличивается – появляется
шарнирно неподвижную опору вместо шарнирно подвижной. При этом число неизвестных составляющих сил реакций увеличивается – появляется 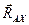 . Трёх уравнений равновесия недостаточно для определения четырёх неизвестных. Поэтому приходится рассматривать равновесие ещё какой-либо части конструкции, например, стержня
. Трёх уравнений равновесия недостаточно для определения четырёх неизвестных. Поэтому приходится рассматривать равновесие ещё какой-либо части конструкции, например, стержня  .
.
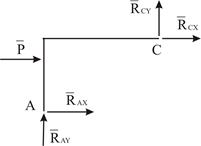
Для стержня  шарнир
шарнир  является внешней опорой, поэтому его реакция входит в систему внешних сил, действующих на
является внешней опорой, поэтому его реакция входит в систему внешних сил, действующих на  (Рис. 2.3). Для стержня
(Рис. 2.3). Для стержня  можно составить ещё три уравнения равновесия, которые вместе с уравнениями равновесия, составленными для арки
можно составить ещё три уравнения равновесия, которые вместе с уравнениями равновесия, составленными для арки 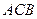 , образуют систему шести уравнений, содержащих шесть
, образуют систему шести уравнений, содержащих шесть
неизвестных.
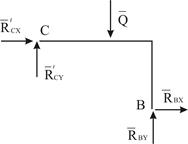
Можно рассмотреть равновесие правого стержня 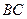 (Рис. 2.4). При этом следует учитывать, что силы взаимодействия в шарнире
(Рис. 2.4). При этом следует учитывать, что силы взаимодействия в шарнире  подчиняются третьему закону Ньютона:
подчиняются третьему закону Ньютона: 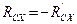 ;
; 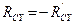 . Для решения поставленной задачи достаточно рассмотреть равновесие только двух из трёх тел в любой комбинации. Условия равновесия третьего тела могут быть использованы для проверки полученных результатов.
. Для решения поставленной задачи достаточно рассмотреть равновесие только двух из трёх тел в любой комбинации. Условия равновесия третьего тела могут быть использованы для проверки полученных результатов.
| 
| |
| Рис. 2.3 | Рис. 2.4 |
Универсальный метод решения подобных задач состоит в том, что конструкция разбивается на отдельные абсолютно твёрдые тела и рассматривается равновесие каждого из этих тел. Однако, во многих случаях такой подход оказывается нерациональным, поскольку приводит к необходимости решения системы уравнений, каждое из которых может содержать несколько неизвестных. Причём в уравнения может входить значительное число лишних неизвестных, которые не требуется определять по условиям решаемой задачи. Приобретя определённые навыки, можно поставить целью поиск наиболее рационального способа решения задачи, в основе которого лежит идея использования минимального числа уравнений, каждое из которых, по возможности, содержит только одну неизвестную.
В заключение подчеркнём ещё раз – необходимо рисовать отдельную силовую схему для каждого тела, равновесие которого рассматривается.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 1906; Нарушение авторских прав?; Мы поможем в написании вашей работы!