
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Практическое занятие № 7
|
|
|
|
Пример
Расчёт ферм
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
Особое место в ряду статических задач занимает расчёт ферм. Фермой называется жёсткая конструкция из прямолинейных стержней. Если все стержни фермы и вся приложенная к ней нагрузка расположены в одной плоскости, ферма называется плоской. В дальнейшем будем рассматривать только плоские фермы. Соединения стержней называются узлами фермы.
В результате полного расчёта фермы необходимо определить реакции опор и усилия во всех стержнях фермы.
При расчёте ферм приложенную внешнюю нагрузку (включая весовую нагрузку) заменяют эквивалентной системой, силы которой приложены к узлам фермы. В реальных фермах соединения стержней, как правило, жёсткие (сварка, клёпка и т.д.), так что они не допускают относительного поворота стержней. В расчётной схеме крепления стержней считаются шарнирными, причём, трение в шарнирах считается пренебрежимо малым.
В результате сделанных упрощающих предположений оказывается, что каждый стержень находится в равновесии под действием двух сил, приложенных к его концам. Эти силы должны иметь общую линию действия, т.е. они направлены вдоль стержня. Таким образом, считается, что каждый стержень фермы работает или на растяжение, или на сжатие, но не может испытывать кручения или изгиба. Усилие в стержне считается положительным, если он растянут.
Для определения усилий в стержнях фермы используются два основных метода.
Рассчитать ферму, изображённую на Рис. 2.18.
Дано:  кН;
кН; 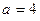 м.
м.

|
| Рис. 2.18 |
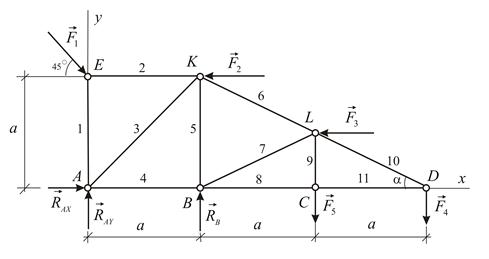
Прежде всего обозначим все узлы и все стержни фермы. Определим реакции опор. Для этого рассмотрим равновесие фермы в целом (Рис. 2.19). Составим условия равновесия:
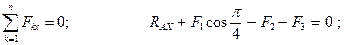
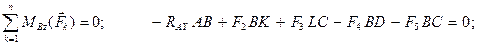
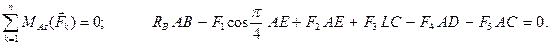
Отсюда:
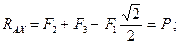

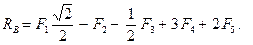
|
| Рис. 2.19 |
Поскольку вычисленные величины опорных реакций определяют весь дальнейший расчёт, имеет смысл проверить полученные результаты, составив, например, уравнение моментов относительно оси  (чтобы в это уравнение вошли все вычисленные величины):
(чтобы в это уравнение вошли все вычисленные величины):

Для определения усилий в стержнях фермы используются два основных метода.
Метод вырезания узлов. Метод состоит в том, что рассматривается равновесие каждого узла фермы в определённой последовательности. На узел действует плоская система сходящихся сил, для которой можно составить два уравнения равновесия, что позволяет определить две неизвестные. Поэтому расчёт начинают с узла, соединяющего два стержня фермы. Затем переходят к соседним узлам в определённой последовательности, которая позволяет на каждом шаге определять усилия в очередных двух стержнях. Первоначально предполагается, что стержни растянуты, т.е. их реакции направлены от узлов. Если усилие в каком-либо стержне оказывается отрицательным, то это означает, что данный стержень сжат.
Заметим, что уравнения равновесия фермы в целом являются прямым следствием полной системы уравнений равновесия узлов, так что методом вырезания узлов можно определить в том числе и реакции опор фермы. Но в этом случае часто приходится совместно решать систему, содержащую значительное число уравнений. Предварительное определение реакций опор упрощает решение задачи, а неиспользованные уравнения равновесия узлов можно рассматривать как проверочные.
Рассмотрим равновесие узла 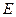



Отсюда: 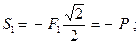 (стержень сжат)
(стержень сжат)
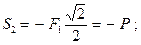 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 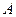

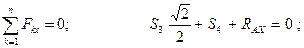

Отсюда:
 (стержень растянут)
(стержень растянут)
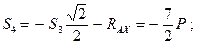 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 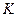


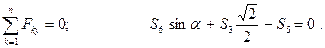
Значения тригонометрических функций определим из треугольника 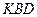 :
:


Таким образом,
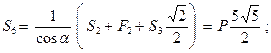 (стержень растянут)
(стержень растянут)
 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 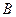

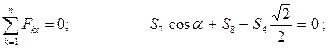
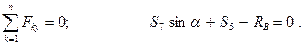
Отсюда:
 (стержень сжат).
(стержень сжат).
 (стержень сжат).
(стержень сжат).
 Рассмотрим равновесие узла
Рассмотрим равновесие узла 


Отсюда:
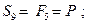 (стержень растянут)
(стержень растянут)
 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 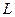


Отсюда:
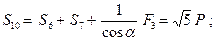 (стержень растянут)
(стержень растянут)
Таким образом, определены усилия во всех стержнях фермы. Оставшиеся уравнения используем для проверки полученных результатов.
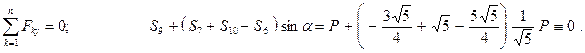
 Рассмотрим равновесие узла
Рассмотрим равновесие узла 


Метод сквозных сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчётов. Идея метода состоит в том, что ферма разделяется сечением на две части и рассматривается равновесие одной из этих частей. Сечение проводится по трём стержням фермы, в которых (или в одном из которых) требуется определить усилие. Действие отброшенной части фермы заменяют соответствующими реакциями, направляя их вдоль разрезанных стержней от узлов, т.е. считая стержни растянутыми (как и в методе вырезания узлов). Условия равновесия составляются так, чтобы в каждое уравнение входила только одна неизвестная величина.
Если сечение проводится более, чем по трём стержням, то усилия в "лишних" стержнях должны быть определены предварительно. В противном случае будет необходимо рассмотреть комбинацию из нескольких сечений или комбинацию метода сечений и метода вырезания узлов.
В качестве примера проведём сечение через шестой, седьмой и восьмой стержни. Рассмотрим равновесие правой части фермы (Рис. 2.20).
Уравнения равновесия имеют вид:
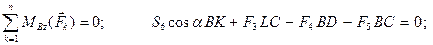

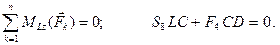
Отсюда:


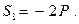

|
| Рис. 2.20 |
Условие жёсткости фермы. Найдём минимальное число стержней 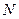 , которое необходимо для образования плоской фермы, имеющей
, которое необходимо для образования плоской фермы, имеющей 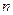 узлов. Простейшая ячейка фермы (треугольник) имеет три стержня и три узла. Для присоединения каждого из оставшихся
узлов. Простейшая ячейка фермы (треугольник) имеет три стержня и три узла. Для присоединения каждого из оставшихся  узлов необходимо два стержня. Таким образом, условие жёсткости фермы имеет вид:
узлов необходимо два стержня. Таким образом, условие жёсткости фермы имеет вид: 
Условие статической определимости фермы. Ферма является статически определимой, если число неизвестных совпадает с числом независимых уравнений равновесия, в которые эти неизвестные входят. Для плоской фермы, имеющей 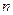 узлов, можно составить
узлов, можно составить  уравнений равновесия, три из которых расходуются на определение трёх составляющих реакций опор. Для определения усилий в стержнях фермы остаётся
уравнений равновесия, три из которых расходуются на определение трёх составляющих реакций опор. Для определения усилий в стержнях фермы остаётся  уравнения. Таким образом, условие статической определимости фермы совпадает с условием её жёсткости.
уравнения. Таким образом, условие статической определимости фермы совпадает с условием её жёсткости.
Методы расчёта фермы рассмотрим на примере.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
- В чём суть упрощающих предположений, принимаемых при расчёте фермы?
- В чём состоит метод вырезания узлов?
- В чём состоит метод сквозных сечений?
- Каково условие жёсткости фермы?
- Каково условие статической определимости фермы?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 4.66; 4.67; 4.68; 4.70; 4.71; 4.73; 4.74.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-8; СР-9; СР-10; СР-11.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 1320; Нарушение авторских прав?; Мы поможем в написании вашей работы!