Свойства средней арифметической величины

Характеристики степенных средних

Вид степенной средней

Показатель степени (m)

Формулы расчета

простая

взвешенная

гармоническая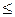

-1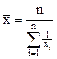

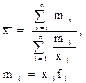
геометрическая £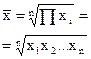

 

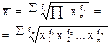
арифметическая £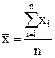

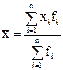
квадратическая

£

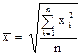
кубическая £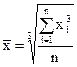

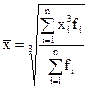
При выборе вида средней величины обычно исходят из логической сущности осредняемого признака и его взаимосвязи с итоговым показателем.

Весом может быть и частость, т.е. отношение частоты повторения индивидуального значения признака (f_i) к сумме частот (Sf_i):

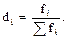(6.2)

Чем больше показатель степени m, тем больше и величина соответствующей средней:

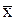_гар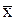м< _геом< 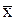_арифм< 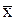_кв< 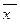_куб. (6.3)

Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних.

1) Средняя арифметическая постоянной величины равна этой постоянной:

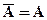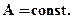при (6.4)

Пусть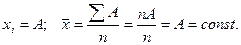

2) Общий множитель индивидуальных значений признака может быть вынесен за знак средней:

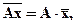(6.5)

т.к.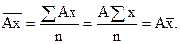

3) Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:

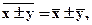т.к.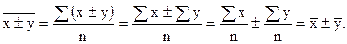

4) Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

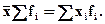(6.7)

5) Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю (нулевое свойство):

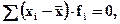(6.8)

6) .

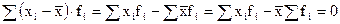Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

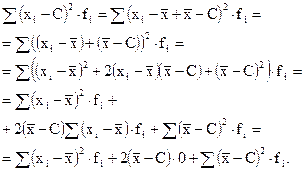(6.9)

7) Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:

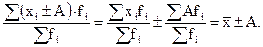(6.10)

8) Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:

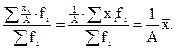(6.11)

9) Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:

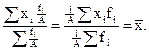(6.12)

При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.

Средняя арифметическая, взвешенная по способу моментов:

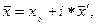(6.13)

где х ₀ – условный нуль;

i – величина, на которую делят разность между значениями вариантов и условным нулем (х - х₀);

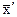- момент первого порядка, определяемый по формуле

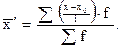(6.14)

Этот способ называют способом отсчета от условного нуля.

Дата добавления: 2015-05-29