
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Показатели вариации, имеющие наиболее широкое применение
|
|
|
|
Понятие вариации
Вопросы к изучению
Показатели вариации
1. Понятие вариации.
2. Показатели вариации, имеющие наиболее широкое применение.
3. Виды и свойства дисперсии.
4. Дисперсия альтернативного признака.
Средняя величина – это абстрактная, обобщающая характеристика признака изучаемой совокупности, она не показывает строения совокупности, которое весьма существенно для её познания. Она не даёт представления о том, как отдельные значения изучаемого признака группируются вокруг средней.
Колеблемость отдельных значений характеризуют показатели вариации. Вариация означает «изменение, колеблемость, различие» (лат.). Под вариацией понимаются такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.
Для измерения вариации признака в совокупности явлений применяются абсолютные, относительные и средние показатели.
К абсолютным и средним показателям относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и квартильное отклонение. Показатели вариации относятся к числу обобщающих показателей.
Размах вариации, или размах колебания (R), представляет собой разность между максимальным (Хmax) и минимальным (Хmin) значениями признака в изучаемой совокупности:
R = Xmax – Xmin. (7.1)
Достоинство этого показателя заключается в простоте его расчёта. Недостаток – из-за того, что он зависит от величины только крайних значений признака, область его применения ограничена достаточно однородными совокупностями. Он не отражает отклонений всех вариантов в ряду.
Различия всех единиц изучаемой совокупности учитывает среднее линейное отклонение (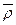 ), для нахождения которого используется арифметическая сумма отклонений без учёта их знаков, и для
), для нахождения которого используется арифметическая сумма отклонений без учёта их знаков, и для
несгруппированных  (простое) (простое)
| (7.2) |
сгруппированных данных 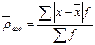 (взвешенное) (взвешенное)
| (7.3) |
Этот показатель дает обобщенную характеристику распределению отклонений. Так как этот показатель не устанавливает степень рассеивания, то он применяется редко. Чем меньше величина среднего линейного отклонения, тем однороднее исследуемая совокупность. Более объективно меру вариации отражает показатель дисперсии (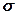 2) - средняя из отклонений вариантов значений признака от их средней величины, возведенных в квадрат, как для, так и для
2) - средняя из отклонений вариантов значений признака от их средней величины, возведенных в квадрат, как для, так и для
несгруппированных 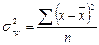 , ,
| (7.4) |
сгруппированных данных 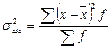 , ,
| (7.5) |
Формулу для расчёта дисперсии можно преобразовывать следующим образом:
 (7.6)
(7.6)
Формула центрального момента второго порядка:
 . (7.7)
. (7.7)
При использовании этой формулы исключается ошибка в расчёте, связанная с округлением отклонений 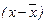 .
.
Корень квадратный из дисперсии представляет собой среднее квадратическое отклонение. Он является мерилом надежности средней. Чем меньше  , тем лучше средняя арифметическая отражает всю совокупность.
, тем лучше средняя арифметическая отражает всю совокупность.
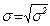 . (7.8)
. (7.8)
Все эти показатели, кроме  2, являются величинами именованными. Среднее квадратическое отклонение показывает, как расположена основная масса единиц совокупности относительно средней арифметической. По способу моментов
2, являются величинами именованными. Среднее квадратическое отклонение показывает, как расположена основная масса единиц совокупности относительно средней арифметической. По способу моментов  .
.
Изложенный способ расчёта дисперсии и среднего квадратического отклонения называется способом моментов, или способом отсчёта от условного нуля. Он применим при условии равных интервалов. Если средняя величина отражает тенденцию развития, т.е. действие главных причин (факторов), то силу воздействия прочих факторов измеряет среднее квадратическое отклонение. Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях. Расчёт показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической (медиане), умножаемое на 100 %.
1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:
 . (7.9)
. (7.9)
2. Относительное линейное отклонение характеризует долю усреднённого значения абсолютных отклонений от средней величины:
 . (7.10)
. (7.10)
3. Коэффициент вариации является наиболее распространённым показателем колеблемости, используемым для оценки типичности средних величин.
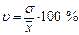 . (7.11)
. (7.11)
Если  > 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
> 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
Если в качестве показателя центра распределения используется медиана, то для характеристики вариации признаков в совокупности можно применить так называемое квартильное отклонение Q.
 , (7.12)
, (7.12)
где Q1 и Q3 – соответственно первая и третья квартили распределения.
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25 % единиц совокупности будут меньше по величине Q1; 25 % единиц будут заключены между Q1 и Q2 ; 25 % - между Q2 и Q3 и остальные 25 % превосходят Q3. Квартили определяются по формулам для расчёта медианы
 , (7.13)
, (7.13)

 , (7.14)
, (7.14)
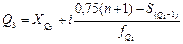 , (7.15)
, (7.15)
где ХQ1 ,XQ2, XQ3 – нижняя граница интервала, где находится соответствующая квартиль;
SQ1 – 1, SQ2 – 1, SQ3 – 1 – сумма накопленных частот интервалов, предшествующих интервалу, где находится первая, вторая и третья квартиль;
fQ1, fQ2, fQ3 – частота интервала, где находится первая, вторая и третья квартиль.
В симметричных или умеренно асимметричных распределениях
Q»  s. Показатель квартильного отклонения может быть рекомендован для рядов распределения с открытыми интервалами. При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации.
s. Показатель квартильного отклонения может быть рекомендован для рядов распределения с открытыми интервалами. При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 656; Нарушение авторских прав?; Мы поможем в написании вашей работы!