Парная регрессия на основе метода наименьших квадратов и метода группировок

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними может описываться одним из уравнений (8.1)-(8.3).

Определить тип уравнения можно, исследуя зависимость графически. Однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи – гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия. Оценка параметров уравнений регрессии (а₀, а₁, и а₂ – в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели (а₀, а₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии

S = å(у -`у_х)² ® min. (8.4)

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид

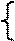na₀+a₁åx = åy,

a₀åx+a₁åx² = åxy, (8.5)

где n – объём исследуемой совокупности.

В уравнениях регрессии параметр а₀ показывает усреднённое влияние на результативный признак неучтённых в уравнении факторных признаков. Коэффициент регрессии а₁ показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения. На практике исследования часто проводятся по большому числу наблюдений. В этом случае исходные данные удобнее представлять в сводной групповой таблице. При этом анализу подвергаются сгруппированные данные и по факторному (х), и по результативному (у) признакам, то есть уравнения парной регрессии целесообразно строить на основе сгруппированных данных.

Если значения х и у заданы в определённых интервалах (a,b), то для каждого интервала сначала необходимо определить середину (х’ / y’ = (a+b) / 2), а затем уже коррелировать значения х’ и у’ и строить уравнения регрессии между ними.

Система нормальных уравнений для определения коэффициентов уравнения регрессии примет вид

na₀+a₁åxf_x = åyf_y,

a₀åxf_x+a₁åx²f_x=åxyf_y, (8.6)

где n – число анализируемых предприятий;

f_x / f_y – число предприятий, согласно распределению, соответственно по факторному и результативному признакам;

уf_y / xf_x – значения результативного и факторного признака по конкретной группе предприятий.

Система нормальных уравнений для нахождения параметров уравнении параболы второго порядка методом наименьших квадратов имеет следующий вид

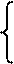na₀+a₁åx + а₂åx² = åy,

a₀åx+a₁åx² + а₂åx³ = åxy, (8.7)

а ₀ åx²+ a₁åx³ + а₂åx⁴ = åx ²y,

Дата добавления: 2015-05-29